Теплоотдача при поперечном обтекании труб

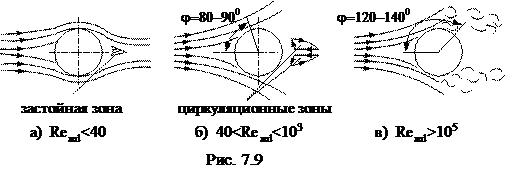Процесс теплоотдачи при поперечном обтекании трубы характеризуется рядом особенностей, которые связаны с гидродинамикой движения жидкости вблизи поверхности трубы (рис.7.9).

Гидродинамика движения жидкости определяется числом Rе_жd=wd/v, где d – наружный диаметр трубы.

При небольших скоростях потока жидкости (Rе_жd <40) обтекание трубы плавное, при более высоких скоростях (40< Rе_жd<10³) происходит отрыв ламинарного пограничного слоя от поверхности трубы, угол отрыва
φ=80-90^о. При значениях Rе_жd>10⁵ ламинарное течение в пограничном слое сменяется турбулентным, угол отрыва турбулентного пограничного слоя от поверхности трубы составляет φ=120-140^о.

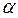Образующийся на поверхности трубы пограничный слой имеет наименьшую толщину в лобовой точке и далее постепенно нарастает до тех пор, пока не произойдет отрыв потока. Характер изменения коэффициента теплоотдачи =f(φ) для позиций рис.7.9 а, б, в показан на рис. 7.10.

Коэффициент теплоотдачи принимает наибольшее значение на лобовой части трубы, где толщина пограничного слоя минимальная.

Из-за увеличения толщины пограничного слоя по периметру трубы коэффициент теплоотдачи уменьшается, достигая минимального значения в точке отрыва потока. В области циркуляционной зоны происходит увеличение коэффициента теплоотдачи за счет разрушения пограничного слоя. Для случая (в) первое увеличение коэффициента теплоотдачи связано со сменой режима течения в пограничном слое, второе – с отрывом турбулентного пограничного слоя.

Для расчета среднего по периметру трубы коэффициента теплоотдачи рекомендуются следующие уравнения:

- при Rе_жd<40

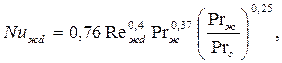(7.31)

- при 40< Rе_жd<10³

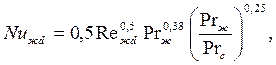(7.32)

- при 10³< Rе_жd<2 ∙10⁵

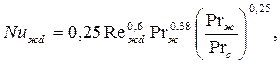(7.33)

- при 2 ∙10⁵< Rе_жd<10⁷

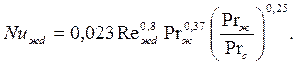(7.34)

Формулы (7.31) – (7.34) действительны для случая, когда угол ψ между направлением потока жидкости и осью трубы, называемый углом атаки, равен 90^о. Если ψ<90^о, то найденный по этим формулам коэффициент теплоотдачи следует умножить на поправочный коэффициент ε_ψ=1- 0,54 cos² ψ.

В теплообменниках трубы располагаются в виде коридорных или шахматных пучков (рис.7.11).

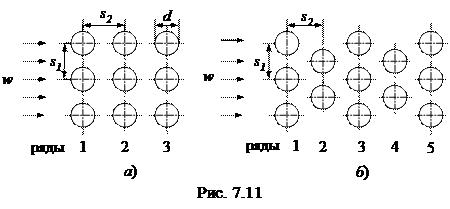Геометрическими характеристиками пучка являются: поперечный (s₁) и продольный (s₂) шаги, наружный диаметр трубы (d), количество рядов труб (п) по направлению движения жидкости.

Режим течения жидкости в пучках может быть ламинарным, турбулентным или смешанным и определяется числом Rе_жd=wd/v, где d – наружный диаметр трубы.

При Rе_жd<10³ – ламинарный режим;

при Rе_жd>10⁵ – турбулентный;

при 10³ <Rе_жd<10⁵ – смешанный.

Экспериментальными исследованиями теплоотдачи в пучках установлено следующее:

1. При ламинарном режиме теплоотдача шахматных пучков выше, чем коридорных, при смешанном режиме эта разница уменьшается. При турбулентном режиме теплоотдача шахматных и коридорных пучков практически одинакова.

2. С увеличением номера ряда пучка теплоотдача возрастает благодаря увеличению турбулентности потока при прохождении его через пучок.

Начиная с третьего ряда и далее, структура потока остается практически неизменной и коэффициент теплоотдачи принимает постоянное значение.

Средние коэффициенты теплоотдачи для третьего и последующих рядов в пучках при поперечном омывании труб потоком жидкости рассчитываются по следующим уравнениям.

Для коридорных пучков:

- при 40<Rе_жd<10³ – ламинарный режим,

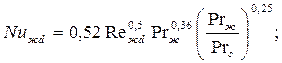(7.35)

- при 10³<Rе_жd<10⁵ – смешанный режим,

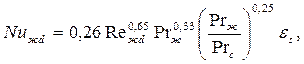(7.36)

где ε_s=(s₂/d)^-0,15 – поправочный коэффициент, учитывающий плотность расположения труб в пучке;

- при Rе_жd>10⁵ – турбулентный режим,

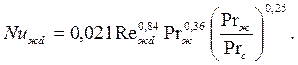(7.37)

Коэффициент теплоотдачи первого ряда коридорного пучка 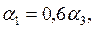второго - 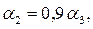где 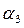- коэффициент теплоотдачи третьего и последующих рядов.

Для шахматных пучков:

- при 40< Rе_жd<10³

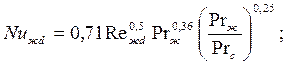(7.38)

- при 10³<Rе_жd<10⁵

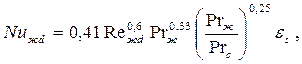(7.39)

если s₁/s₂<2, то ε_s=(s₁/s₂)^1/6,

если s₁/s₂ 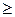2, то ε_s=1,12;

- при Rе_жd>10⁵ коэффициент теплоотдачи шахматных пучков рассчитывается по уравнению (7.37).

Коэффициент теплоотдачи первого ряда шахматного пучка 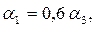второго -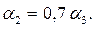

Уравнения (7.35) – (7.39) справедливы для угла атаки ψ=90^о. При ψ<90^о уменьшение коэффициента теплоотдачи следует учесть коэффициентом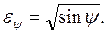

Конвективный теплообмен между трубами пучка и потоком жидкости рассчитывают по уравнению

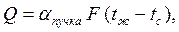(7.40)

где F, м² – площадь поверхности всех труб пучка.

Средний коэффициент теплоотдачи пучка рассчитывается по формуле

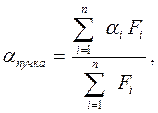где п – число рядов.

При одинаковом числе труб в ряду (F₁=F₂=…=F_n)

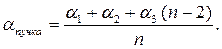(7.41)

Контрольные вопросы и задания

1. Для парового котла высотой h=14 м с температурой поверхности обмуровки t_c=40^оС и температурой воздуха в цехе t_ж=20^оС определите режим течения жидкости (воздуха) в пограничном слое при х= h.

Какие режимы течения жидкости имеют место по высоте поверхности обмуровки и какова протяженность участков с этими режимами?

2. Выведите формулы (7.12) и (7.13) с учетом (7.8) – (7.10) и уравнения теплового баланса Q_экв=Q_к+т+Q_л.

3. Можно ли уравнениями (7.20) и (7.21) воспользоваться для расчетов коэффициентов теплоотдачи:

а) при омывании труб продольным потоком жидкости;

б) при расчетах теплообмена между обшивкой летящего самолета и потоком воздуха, омывающего поверхность обшивки?

4. Какие режимы и при каких условиях имеют место в случае вынужденного течения жидкости в трубах? Сравните по коэффициенту теплоотдачи ламинарный и турбулентный режимы, вязкостный и вязкостно-гравитационный режимы. Дайте обоснование ответа.

5. Запишите формулу для определения коэффициента теплоотдачи при стабилизированном турбулентном течении жидкости в трубе. Подставьте в нее значения чисел Nu=ad/l, Re=wd/v, Pr=v/a=(v×c_pr)/l и сделайте анализ зависимости

a=f (d, w, l, v, cp, r).

6. Сравните коэффициенты теплоотдачи при омывании трубы поперечным вынужденным потоком жидкости для угла атаки y=90^о и y=60^о. Во сколько раз они отличаются?

7. При каком режиме течения жидкости на теплоотдачу влияет плотность расположения труб в пучке?

Примеры решения задач

Задача № 1. Определить тепловые потери от паропровода диаметром d=200мм и длиной =20 м, проложенного в закрытом помещении с температурой воздуха t_ж=30^оС. Температура наружной стенки паропровода t_с=150^оС.

Учесть потерю теплоты излучением. Степень черноты поверхности паропровода принять ε=0,9.

Решение

Здесь имеет место теплоотдача при естественной конвекции в большом объеме. При температуре t_ж=30^оС для воздуха из табл.1 приложения имеем:

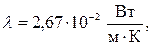
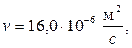Pr_ж=0,701,

при t_с=150^оС находим Pr_с=0,683.

Температурный коэффициент объемного расширения воздуха вычисляем по формуле

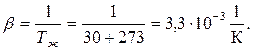Находим произведение

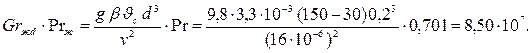Так как (Gr_жd·Pr_ж)<10⁹, то средний коэффициент теплоотдачи рассчитываем по уравнению (7.7):

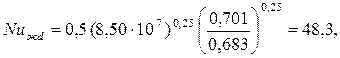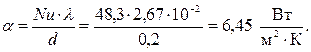Сомножитель для воздуха, 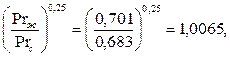практически равен 1, поэтому для газов им можно пренебрегать.

Потери тепла конвекцией

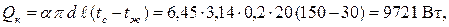излучением

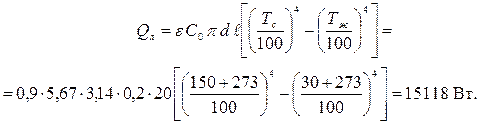Суммарные тепловые потери паропровода составляют

Q=Qк+Qл=24838 Вт.

Задача № 2. Определить плотность теплового потока, проходящего через вертикальную щель толщиной δ=10 мм, заполненную воздухом. Температура горячей поверхности t₁=180^оС, степень черноты ε₁=0,9, холодной – t₂=60^оС, ε₂=0,5.

Решение

Между поверхностями, разделенными воздушной прослойкой, теплота передается теплопроводностью, конвекцией и излучением и может быть рассчитана по формуле

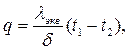где λ_экв=λ ε_к+q_л δ/(t₁-t₂).

При средней температуре воздуха 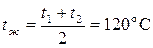из табл. 1 приложения находим

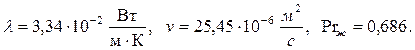
Определяем температурный коэффициент объемного расширения

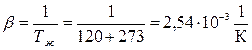и рассчитываем произведение чисел подобия

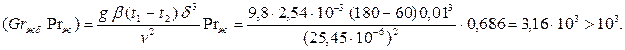Коэффициент конвекции

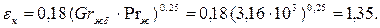
Рассчитываем приведенную степень черноты поверхностей

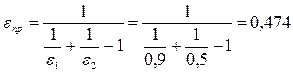
и плотность лучистого потока

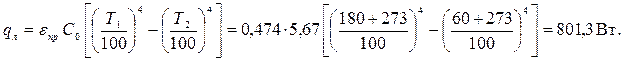Тогда

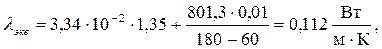
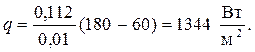
Задача № 3. По трубке внутренним диаметром 8 мм и длиной =5м движетсявода со скоростью w=1,2м/с. Температура поверхности трубки t_с=90^оС, средняя температура воды в ней 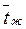=30^оС.

Определить коэффициент теплоотдачи и тепловой поток, передаваемый от стенки трубки к воде.

Решение

При средней температуре воды в трубке 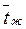=30^оС из табл. 2 приложения имеем:

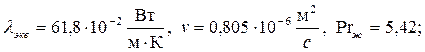при температуре стенки t_с=90^оС Pr_c=1,95.

Определяем число Рейнольдса

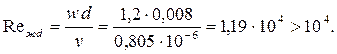Режим течения турбулентный. По уравнению (7.28) рассчитываем средний коэффициент теплоотдачи от стенки трубки к воде. Так как /d=5/0,008=625>50, то =1,

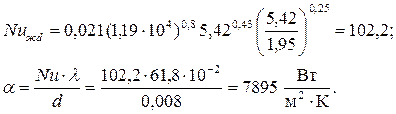Тепловой поток
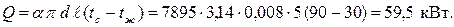