Уравнения Колмогорова

Рассмотрим математическое описание марковского случайного процесса с дискретными состояниями системы S₀, S₁, S₂ (см. рис. 6.2.1) и непрерывным временем. Полагаем, что все переходы системы массового обслуживания из состояния S_i в состояние S_j происходят под воздействием простейших потоков событий с интенсивностями l_ij, а обратный переход — под воздействием другого потока l_ij, Введем обозначение р_i как вероятность того, что в момент времени t система находится в состоянии S_i. Для любого момента времени t справедливо записать нормировочное условие — сумма вероятностей всех состояний равна 1:

S p_i(t) = p₀(t) + p₁(t) + p₂(t) = 1.

i=0

Проведем анализ системы в момент времени t, задав малое приращение времени Dt, и найдем вероятность p₁(t + Dt) того, что система в момент времени (t + Dt) будет находиться в состоянии S₁, которое достигается разными вариантами:

а) система в момент t с вероятностью p_i(t) находилась в состоянии S_i и за малое приращение времени Dt так и не перешла в другое соседнее состояние — ни в S₀, ни в S₂. Вывести систему из состояния S₁ можно суммарным простейшим потоком с интенсивностью (l₁₀ + l₁₂) , поскольку суперпозиция простейших потоков также является простейшим потоком. На этом основании вероятность выхода из состояния S₁ за малый промежуток времени Dt приближенно равна (l₁₀ + l₁₂)×Dt. Тогда вероятность невыхода из этого состояния равна [1 — (l₁₀ + l₁₂) × Dt]. В соответствии с этим вероятность того, что система останется в состоянии S₁ на основании теоремы умножения вероятностей, равна:

p₁(t)[l – (l₁₀ + l₁₂)×Dt];

б) система находилась в соседнем состоянии S₀ И за малое время Dt перешла в состояние S₁. Переход системы происходит под воздействием потока l₀₁ c вероятностью, приближенно равной l₀₁ Dt.

Вероятность того, что система будет находиться в состоянии S₁, в этом варианте равна p₀(t) l₀₁Dt;

в) система находилась в состоянии S₂ и за время Dt перешла в состояние S₁ под воздействием потока интенсивностью l₂₁ с вероятностью, приближенно равной l₂₁Dt. Вероятность того, что система будет находиться в состоянии S₁, равна p₂(t)l₂₁Dt.

Применяя теорему сложения вероятностей для этих вариантов, получим выражение:

p₁(t + Dt) = p₁(t)[1 – (l₁₀ + l₁₂ ) Dt] + p₀(t) l₀₁Dt + p₂(t)l₂₁Dt,

которое можно записать иначе:

p₁(t + Dt) – p₁(t) ₌ p₀(t)l₀₁ + p₂(t)l₂₁ – p₁(t)(l₁₀ + l₁₂).

Переходя к пределу при А/ -^ О, приближенные равенства перейдут в точные, и тогда получим производную первого порядка

dp₁ ₌ p₀l₀₁ + p₂l₂₁ – p₁(l₁₀ + l₁₂),

d_t

что является дифференциальным уравнением.

Проводя рассуждения аналогичным образом для всех других состояний системы, получим систему дифференциальных уравнений, которые называются уравнениями А.Н. Колмогорова:

Для составления уравнений Колмогорова существуют общие правила.

Уравнения Колмогорова позволяют вычислить все вероятности состояний СМО S_i в функции времени p_i(t). В теории случайных процессов показано, что если число состояний системы конечно, а из каждого из них можно перейти в любое другое состояние, то существуют предельные (финальные) вероятности состояний, которые показывают на среднюю относительную величину времени пребывания системы в этом состоянии. Если предельная вероятность состояния S₀ равна p₀ = 0,2, то, следовательно, в среднем 20% времени, или 1/5 рабочего времени, система находится в состоянии S0. Например, при отсутствии заявок на обслуживание k = 0, p0 = 0,2, следовательно, в среднем 2 ч в день система находится в состоянии S₀ и простаивает, если продолжительность рабочего дня составляет 10 ч.

Поскольку предельные вероятности системы постоянны, то, заменив в уравнениях Колмогорова соответствующие производные нулевыми значениями, получим систему линейных алгебраических уравнений, описывающих стационарный режим СМО. Такую систему уравнений составляют по размеченному графу состояний СМО по следующим правилам: слева от знака равенства в уравнении стоит предельная вероятность р_i рассматриваемого состояния S₁ умноженная на суммарную интенсивность всех потоков, выводящих (выходящие стрелки) из данного состояния S_i систему, а справа от знака равенства — сумма произведений интенсивности всех потоков, входящих (входящие стрелки) в состояние S_i систему, на вероятность тех состояний, из которых эти потоки исходят. Для решения подобной системы необходимо добавить еще одно уравнение, определяющее нормировочное условие, поскольку сумма вероятностей всех состояний СМО равна 1:

S p_i(t)=1

i=1

Например, для СМО, имеющей размеченный граф из трех состояний S₀, S₁, S₂ рис. 6.2.1, система уравнений Колмогорова, составленная на основе изложенного правила, имеет следующий вид:

Выходящие Входящие

Для состояния S₀® p₀ – l₀₁ = p₁×l₁₀

Для состояния S₁® (l₁₀ + l₁₂) = p₀l₀₁ + p₁l₂₁

Для состояния S₂® p₂l₂₁ = p₁l₁₂

p₀ + p₁ + p₂ = 1

Пример 1. Составим систему уравнений Колмогорова в общем виде для случая, когда граф состояний имеет вид (рис. 6.2.2):

Плотность вероятностей этих переходов указана рядом с соответствующими стрелками. Пользуясь приведенными выше правилами, получаем систему уравнений:

К этим уравнениям надо добавить еще начальные условия. Например, если при t = 0 система S находится в состоянии S₁, то начальные условия можно записать так:

p₁(0) = 1, p₂(0) = p₃(0) = p₄(0) = 0.

Переходы между состояниями СМО происходят под воздействием поступления заявок и их обслуживания. Вероятность перехода в случае, если поток событий простейший, определяется вероятностью появления события в течение времени Dt, т.е. величиной элемента вероятности перехода l_ij Dt, где l_ij — интенсивность потока событий, переводящих систему из состояния / в состояние j (по соответствующей стрелке на графе состояний).

Если все потоки событий, переводящие систему из одного состояния в другое, простейшие, то процесс, протекающий в системе, будет марковским случайным процессом, т.е. процессом без последствия. В этом случае поведение системы достаточно просто определяется, если известны интенсивность всех этих простейших потоков событий. Например, если в системе протекает марковский случайный процесс с непрерывным временем, то, записав систему уравнений Колмогорова для вероятностей состояний и проинтегрировав эту систему при заданных начальных условиях, получим все вероятности состояний как функции времени:

p_i(t), p₂(t), …, p_n(t).

Во многих случаях на практике оказывается, что вероятности состояний как функции времени ведут себя таким образом, что существует

Lim p_i(t) = p_i (i = 1,2, …, n)

t®¥

независимо от вида начальных условий. В этом случае говорят, что существуют предельные вероятности состояний системы при t®¥ и в системе устанавливается некоторый предельный стационарный режим. При этом система случайным образом меняет свои состояния, но каждое из этих состояний осуществляется с некоторой постоянной вероятностью, определяемой средним временем пребывания системы в каждом из состояний.

Вычислить предельные вероятности состояния p_i можно, если в системе положить все производные равными 0, поскольку в уравнениях Колмогорова при t®¥ зависимость от времени пропадает. Тогда система дифференциальных уравнений превращается в систему обычных линейных алгебраических уравнений, которая совместно с нормировочным условием позволяет вычислить все предельные вероятности состояний.

Пример 2. Запишем систему алгебраических уравнений для вычисления предельных вероятностей состояний системы, изображенной на рис. 6.2.2.

Для этого допустим, что

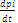Уравнения Колмогорова - student2.ru = 0 (i = 1; 2; 3; 4),

тогда из записанной ранее в примере 1 системы уравнений Колмогорова получаем:

l21p23 - l12p1 =0,

l12p1 + l23p^3 - (l21 + l23)p2 =0,

l23p2 + l43p4 -(l32 +l34)p3 =0,

l34p3 - l43p4=0;

И, Кроме того, мы должны учесть нормировочное условие:

p₁+p₂+p₃+p₄=1

Любое из уравнений записанной системы можно исключить, использовав вместо него нормировочное условие.

Предмет, цель и задачи теории массового обслуживания

Во многих областях экономики, финансов, производства и быта важную роль играют системы специального вида, реализующие многократное выполнение однотипных задач. Подобные системы называют системами массового обслуживания (СМО). В качестве примеров СМО в финансово- экономической сфере можно привести системы, представляющие собой банки, страховые организации, налоговые инспекции, аудиторские службы. В сфере производства и обслуживания примерами СМО могут служить: различные системы связи (телефонные станции), погрузочно-разгрузочные комплексы, автозаправочные станции, магазины, парикмахерские, билетные кассы, пункты обмена валюты, и т.д. Такие системы как компьютерные сети, системы сбора, хранения и обработки информации, системы противовоздушной или противоракетной обороны также могут рассматриваться как своеобразные СМО.

Каждая СМО включает в свою структуру некоторое число обслуживающих устройств, которые называют каналами (приборами, линиями) обслуживания. Роль каналов могут играть различные приборы, лица, выполняющие те или иные операции (кассиры, операторы, парикмахеры), линии связи, машины, краны, ремонтные бригады, железнодорожные пути и т.д.

СМО могут быть одноканальными или многоканальными.

Каждая СМО предназначена для обслуживания (выполнения) некоторого потока заявок (требований), поступающих на вход системы большей частью не регулярно, а случайные моменты времени. Обслуживание заявок, также длится не постоянное, заранее известное время, а случайное время, которое зависит от многих случайных причин. После обслуживания заявки канал освобождается и готов к приему следующей заявки. Случайный характер потока заявок и времени их обслуживания приводит к неравномерной загруженности СМО: на входе СМО могут скапливаться необслуженные заявки, что приводит к перегрузке СМО, а при свободных каналах на входе СМО заявки не будет, что приводит к недогрузке СМО, т.е. к простаиванию ее каналов. Заявки, скапливающиеся на входе СМО, либо «становятся» в очередь, либо по причине невозможности дальнейшего пребывания в очереди покидают СМО необслуженными.

Во всякой СМО можно выделить следующие основные элементы:

1) входящий поток заявок;

2) очередь;

3) каналы обслуживания;

4) выходящий поток обслуженных заявок.

Каждая СМО в зависимости от своих параметров — характера потока заявок, числа каналов обслуживания и их производительности, а также от правил организации работы обладает определенной эффективностью функционирования (пропускной способностью), позволяющей ей более или менее успешно справляться с потоком заявок.

Предметом изучения теории массового обслуживания является СМО.

Цель теории массового обслуживания — выработка рекомендаций по рациональному построению СМО, рациональной организации их работы и регулированию потока заявок для обеспечения высокой эффективности функционирования СМО.

Для достижения этой цели решаются задачи теории массового обслуживания, состоящие в установлении зависимостей эффективности функционирования СМО от ее организации (параметров): характера потока заявок, числа каналов и их производительности и правил работы СМО.

В качестве характеристик эффективности функционирования СМО можно, выбрать три основные группы (обычно средних) показателей:

1. Показатели эффективности использования СМО:

1.1. Абсолютная пропускная способность СМО — среднее число заявок, которое может обслужить СМО в единицу времени.

1.2. Относительная пропускная способность СМО — отношение среднего числа заявок, обслуживаемых СМО в единицу времени, к среднему числу поступивших заявок за это же время.

1.3. Средняя продолжительность периода занятости СМО.

1.4. Коэффициент использования СМО — средняя доля времени, в течение которого СМО занята обслуживанием заявок.

2. Показатели качества обслуживания заявок:

2.1. Среднее время ожидания заявки в очереди.

2.2. Среднее время пребывания заявки в СМО.

2.3. Вероятность отказа заявке в обслуживании без ожидания.

2.4. Вероятность того, что поступившая заявка немедленно будет принята к обслуживанию.

2.5. Закон распределения времени ожидания заявки в очереди.

2.7. Закон распределения времени пребывания заявки в СМО.

2.8. Среднее число заявок, находящихся в очереди.

2.9. Среднее число заявок, находящихся в СМО.

3. Показатели эффективности функционирования пары «СМО — по-требитель», где под потребителем понимают всю совокупность заявок или некий их источник (например, средний доход, приносимый СМО в единицу времени, и т.п.).

Отметим, что третья группа показателей оказывается полезной в тех случаях, когда некоторый доход, получаемый от обслуживания заявок, и затраты на обслуживание измеряются в одних и тех же единицах. Эти показатели обычно носят вполне конкретный характер и определяются спецификой СМО, обслуживаемых заявок и дисциплиной обслуживания.

Случайный характер потока заявок и длительности их обслуживания порождает в СМО случайный процесс.

Случайным процессом (или случайной функцией) называется соответствие, при котором каждому значению аргумента (в данном случае — моменту из промежутка времени проводимого опыта) ставится в соответствие случайная величина (в данном случае — состояние СМО).

Для решения задач теории массового обслуживания необходимо этот случайный процесс изучить, т. е. построить и проанализировать его математическую модель.

Математическое изучение функционирования СМО значительно упрощается, если протекающий в ней случайный процесс является марковским. В этом случае работа СМО сравнительно легко описывается с помощью аппарата конечных систем обыкновенных линейных дифференциальных уравнений первого порядка, а в предельном режиме (при достаточно длительном функционировании СМО) — с помощью аппарата конечных систем линейных алгебраических уравнений, и в результате удается выразить в явном виде основные характеристики эффективности функционирования СМО через параметры СМО, потока заявок и дисциплины работы СМО.

Чтобы случайный процесс был марковским, необходимо и достаточно, чтобы все потоки событий, под воздействием которых происходят переходы системы из состояния в состояние, были пуассоновскими. В СМО потоками событий являются потоки заявок, потоки «обслуживания» заявок и т.д.

6. Потоки событий

Процесс работы СМО представляет собой случайный процесс. Под случайным (вероятностным или стохастическим) процессом понимается процесс изменения во времени состояния какой-либо системы в соответствии с вероятностными закономерностями. Переводы СМО из одного состояния в другое происходят под воздействием событий - поступления заявок и их обслуживания. Последовательность появления событий, следующих одно за другим в случайные моменты времени, формирует так называемый ноток событий. Под потоком событий понимается последовательность однородных событий, следующих одно за другим в случайные моменты времени. Обычно поведение системы обычно определяется не одним, а сразу несколькими потоками. Так, например, обслуживание клиентов в ателье определяется потоком посетителей и потоком обслуживания; в этих потоках случайными явля-ются моменты появления клиентов, время ожидания в очереди и время, затрачиваемое на обслуживание каждого клиента. Поток характеризуется интенсивностью X - частотой появления событий или средним числом событий, поступающих в СМО в единицу времени.

Поток событий называется регулярным, если события следуют одно за другим через определенные равные промежутки времени. Например, поток изделий на конвейере сборочного цеха (с постоянной скоростью движения) является регулярным.

Поток событий называется стационарным, если вероятность появления к событий за промежуток времени длительностью I зависит только от длительности промежутка t и не зависит от начала отсчета. Стационарность потока означает независимость от времени его вероятностных характеристик.

Поток событий называется ординарным, если вероятность попадания на малый (элементарный) участок времени DeltaT двух и более событий пренебрежимо мала по сравнению с вероятностью попадания только одного события. Другими словами, поток событий ординарен, если события появляются в нем поодиночке, а не группами. Например, поток поездов, подходящих к станции, ординарен, а поток вагонов не ординарен.

Поток событий называется потоком без последействия, если для любых двух непересекающихся участков времени t1 и t2 ~ число событий, попадающих на один из них, не зависит от числа событий, попадающих на другие. Например, поток покупателей, входящих в магазин, можно считать потоком без последействия потому, что причины, обусловившие приход каждого из них, не связаны с аналогичными причинами других покупателей.

Поток событий называется простейшим (или пуассоновским), если он одновременно стационарен, ординарен и не имеет последействия. Название "простейший" объясняется тем, что СМО с простейшими потоками имеет

8. Системы массового обслуживания

Классификация систем массового обслуживания

Системы массового обслуживания делятся на типы (или классы) по ряду признаков.

По числу каналов СМО подразделяют на одноканальные (когда име-ется один канал обслуживания) и многоканальные, точнее n-канальные (когда количество каналов n>=2). Здесь и далее будем полагать, что каждый канал одновременно может обслуживать только одну заявку и, если не оговорено специально, каждая находящаяся под обслуживанием заявка обслуживается только одним каналом. Многоканальные СМО могут состоять из однородных каналов, либо из разнородных, отличающихся длительностью обслуживания одной заявки. Практически время обслуживания каналом одной заявки Тоб является непрерывной случайной величиной. Однако при условии абсолютной однородности поступающих заявок и каналов время обслуживания может быть и величиной постоянной (Tоб=const).

По дисциплине обслуживания СМО подразделяют на три класса:

1. СМО с отказами, в которых заявка, поступившая на вход СМО в момент, когда все каналы заняты, получает «отказ» и покидает СМО («пропадает»), Чтобы эта заявка все же была обслужена, она должна снова поступить на вход СМО и рассматриваться при этом как заявка, поступившая впервые. Примером СМО с отказами может служить работа АТС: если набранный телефонный номер (заявка, поступившая на вход) занят, то заявка получает отказ, и, чтобы дозвониться по этому номеру, следует его набрать еще раз (заявка поступает на вход как новая).

2. СМО с ожиданием (неограниченным ожиданием или очередью). В таких системах заявка, поступившая в момент занятости всех каналов, становится в очередь и ожидает освобождения канала, который примет ее к обслуживанию. Каждая заявка, поступившая на вход, в конце концов будет обслужена. Такие СМО часто встречаются в торговле, в сфере бытового и медицинского обслуживания, на предприятиях (например, обслуживание станков бригадой наладчиков).

3. СМО смешанного типа (с ограниченным ожиданием). Это такие системы, в которых на пребывание заявки в очереди накладываются некоторые ограничения.

Эти ограничения могут накладываться на длину очереди, т.е. макси-мально возможное число заявок, которые одновременно могут находиться в очереди. В качестве примера такой системы можно привести мастерскую по ремонту автомобилей, имеющую ограниченную по размерам стоянку для неисправных машин, ожидающих ремонта.

Ограничения ожидания могут касаться времени пребывания заявки в очереди, по истечению которого она выходит из очереди и покидает систему, либо касаться общего времени пребывания заявки в СМО (т.е. суммарного времени пребывания заявки в очереди и под обслуживанием).

В СМО с ожиданием и в СМО смешанного типа применяются различные схемы обслуживания заявок из очереди. Обслуживание может быть упорядоченным, когда заявки из очереди обслуживаются в порядке их поступления в систему, и неупорядоченным, при котором заявки из очереди обслуживаются в случайном порядке. Иногда применяется обслуживание с приоритетом, когда некоторые заявки из очереди считаются приоритетными и поэтому обслуживаются в первую очередь.

По ограничению потока заявок СМО делятся на замкнутые и от-крытые.

Если поток заявок ограничен и заявки, покинувшие систему, могут в нее возвращаться, то СМО является замкнутой, в противном случае - от-крытой. Классическим примером замкнутой СМО служит работа бригады наладчиков в цеху. Станки являются источниками заявок на обслуживание, и их количество ограничено, наладчики - каналы обслуживания. После проведения ремонтных работ вышедший из строя станок снова становится источником заявок на обслуживание. В открытой СМО характеристики потока заявок не зависят от того, в каком состоянии сама СМО (сколько каналов занято). В замкнутой СМО - зависят. Так, в рассмотренном выше примере интенсивность потока «заявок» со стороны станков (т.е. количество заявок в единицу времени) зависит от того, сколько их неисправно и ждет наладки.

По количеству этапов обслуживания СМО делятся на однофазные и многофазные системы.

Если каналы СМО однородны, т.е. выполняют одну и ту же операцию обслуживания, то такие СМО называются однофазными. Если каналы обслуживания расположены последовательно и они неоднородны, так как выполняют различные операции обслуживания (т.е. обслуживание состоит из нескольких последовательных этапов или фаз), то СМО называется многофазной. Примером работы многофазной СМО является обслуживание автомобилей на станции технического обслуживания (мойка, диагностирование и т.д.).

Далее будем рассматривать только однофазные СМО.

48)Игры с природой. Критерий максимального среднего выигрыша (критерий Байеса, критерий Лапласа).

Существуют игры, в которых только один игрок сознательно принимает решения(ЛПР), а другая сторона пассивна, эта сторона сознательно не принимает решения, а с некоторой вероятностью принимает какие либо состояния под влиянием случайных факторов, такого рода ситуации называют играми с природы.

Под природой понимают совокупность неопределенных факторов, влияющих на эффективность принимаемых решений активного игрока.

Существуют игры с природы, в которых известны вероятности возможных состояний, такие игры называют играми в условиях частичной неопределенности. Для выявления оптимальных стратегий активного игрока применяют критерий Байеса.

Если вероятности состояния природы неизвестны, то говорят об игре с природой в условиях полной неопределенности. Тогда для определения оптимальных стратегий активного игрока применяют критерий Лапласа, Вальда, Сэвиджа, Гурвица.

КРИТЕРИЙ БАЙЕСА:

Вероятности состояния природы qj обычно определяется путем проведения экспериментов или наблюдений, поэтому их принято называть апостериорными. В качестве оптимальных стратегий по критерию Байеса принимается чистая стратегия активного игрока, при которой его средний выигрыш становится максимальным. Каждый средний выигрыш будет находится по формуле

Ai= ai1* q1+ ai2*q2+…+ ain* qn

B= max Ai

Критерий Байеса можно рассматривать относительно средних рисков. РИСКОМ называют разность между макс выигрышем активного игрока и обозначаем max aik, который он мог бы получить достоверно зная, что природа примет состояние Пк, а также тем выигрышем, который он получит, используя стратегию Ai ( т.е., чтобы составить матрицу рисков необходимо по каждому столбцу платежной матрицы найти max элемента, а затем вычитать из него соответствующие выигрыши платежной матрицы.

rij= max aik- aik

В матрице рисков каждый столбец будет содержать хотя бы один нулевой элемент. По критерию Байеса определим средние риски активного игрока.

Ri= ri1* q1 +ri2* q2+..+rin* qn .

Оптимальной будет считаться та стратегия, при которой достигается минимальный средний риск R= min Ri.

Критерий Лапласа аналогичен критерию Байеса, но вероятности состояния природы неизвестны, поэтому предполагается, что все состояния природы равновероятны, т.е. q1=q2=…=qn=1/n

Ai=1/n (ai1 +ai2+…+ain)

L= max Ai

Ri= 1/n( ri1+ri2+…+rin)

49. Игры с природой. Критерий Вальда. Критерий Сэвиджа. Игры с природой. Критерий Гурвица.

Критерий Вальда- критерий крайнего пессимизма, т.к активному игроку предлагают выбрать ту стратегию, при которой наименьший выигрыш будет максимальным.

Wi=min aij

W= maxWi=max min aij

Критерий Сэвиджа- как и критерий Вальда, крайнего пессимизма, но он опирается не на исходную платежную матрицу, а матрицу рисков, значит по каждой строке нужно найти максимальный риск, а затем из всех максимальных рисков минимальный.

Si=max rij

S=min Si=min max rij

Критерий Гурвица. Можно рассматривать критерий крайнего пессимизма (Вальда и Сэвиджа), а можно рассмотреть критерий крайнего оптимизма (максимаксные критерии), однако лучше придерживаться золотой середины.

К.Г. является критерием пессимизма-оптимизма.

В начале по каждой стратегии активного игрока рассчитывается показатель. Оптимальной по критерию Гурвица является та стратегия для которой значения Gi будет max

G=max Gi=max( min aij+ (1-) max aij)

При =1 критерий Гурвица переходит в критерий Вальда, а при получаем максимальный критерий, или критерий максимального оптимизма.

Остальные промежуточные значения  в большую или меньшую сторону смещены ими к оптимуму или пессимизму.

При желании подстраховаться  следует выбирать ближе к 1, а близкие к 0 дают более рискованный результат.