Параметрические уравнения поверхности эллипсоида
Внешний вид любого тела вращения характеризуется его образующей.
В канонической форме уравнение поверхности эллипсоида представляется известной формулой
x2 / a2 + y2 / a2 +z2 / b2 = 1,
где a – большая (экваториальная) полуось эллипсоида, b – малая (полярная) полуось, x, y, z – координаты точки поверхности эллипсоида. (Для точки на полюсе: х =у=0, z = b; )
для точки на экваторе: х = а, у = z = 0)
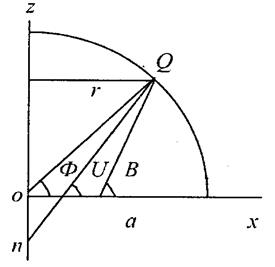
Сечения поверхности эллипсоида плоскостями, перпендикулярными к оси вращения представляют собой окружности, называемые параллелями. Наибольшая из них, проходящая через центр эллипсоида, называется экватором.
Плоскости, проходящие через ось вращения называются меридианными плоскостями. Следы сечения ими поверхности эллипсоида представляют собой эллипсы и называются меридианами.
В математике рассматривают множество элементов, характеризующих эллипсоид. Здесь мы рассмотрим только те, которыми наиболее часто пользуются в теории и практике раздела сфероидической геодезии.
Достаточно знать значения параметров только двух элементов эллипсоида, чтобы определить значения других параметров.
Основнымиопределяющими элементами земного эллипсоида в геодезии принято считать его большую полуось “а” и полярное сжатие “α”. Зная параметры этих двух элементов земного эллипсоида можно определить параметры остальных, используемых в геодезии его элементов.
Из математики известно, что расстояние от центра эллипса до
-----------------
каждого из его фокусов, равное √(a2 – b2) =аe, называется линейным эксцентриситетом.
р



 а а
а а
 F2 b F1
F2 b F1
а
p1
Отношение линейного эксцентриситета к большой и малой
полуосям называют соответственно:
…………..
первым эксцентриситетом: е= 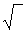 (a2 - b2) /а или e2 = (a2 –b2)/ a2 ;
(a2 - b2) /а или e2 = (a2 –b2)/ a2 ;
…………..
и вторым - е1 = 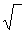 (a2 - b2) /b или (e1)2 = (a2 –b2)/ b2
(a2 - b2) /b или (e1)2 = (a2 –b2)/ b2
соответственно.
(для эллипсоида Красовского:
e2 = 0,0066934216и (e1)2 = 0,0067385254.
Полуоси определяют размеры эллипсоида, а эксцентриситет – его форму. Чем больше разность между полуосями, тем больше эксцентриситеты. У шара при (a=b) они равны нулю.
Форма эллипсоида определяется также значением сжатия α (полярным сжатием)
α = (a - b)/ a.
Отсюда следует, что разность полуосей определяется простым выражением: (a - b) = αа.(для эллипсоида Красовского:α = 0,0033523299, а = 6 378 245 м; (a - b) = 21, 381,9812 км).
эллипсоида Красовского полярный радиус кривизны с
Таким образом, эллипсоид вращения вполне определяется двумя его элементами: либо значениями полуосей, либо значением одного линейного элемента (обычно значением большой полуоси) и сжатием.
Кроме того, в геодезии часто используют вспомогательные функции “c” и “p” вида
с = а2 / b (полярный радиус кривизны) и p = b2/a, равенство η = e1 cos B –выражения для кривизны кривой.
(для = 6 399 698,9018 м).
Для приближенных расчетов полезно знать: а = 6 400 км,
(a - b) = 21 км, α = 1/300, а2 = 1/150.
В теории сфероидической геодезии используется разложение функций в ряды по степени эксцентриситета. Например, при установлении числа членов разложения в ряд полезно знать, что произведение: ае2 = 43 км (если принять е2 = 2α, то приблизительно: ае2 = 2(а –b); так как (а –b) примерно 21,5 км), то
ае2 = 43 км; ае4 = 290 м; ае6 = 2 м: ае8 = 12 мм .
Тогда в рядах обычно ограничиваются членом с ае8.
Запись многих формул сфероидической геодезии существенно упрощается введением специальных выражений, называемых основными сфероидическими функциями:
первая W2 = (1 – е2sin2B); вторая V2 = (1 + (e1)2 cos2B).
Связь между фунциями:
W2= (1 – е2 sin2B) = (1 – е2) V2 = (b / a )2 V2,
 V2 = (1 + (e1)2 cos2B) = (1 + (e1)2) W2 = (a / b)2W2, откуда получаем выражение для контроля вычисления W и V: Wa = Vb.
V2 = (1 + (e1)2 cos2B) = (1 + (e1)2) W2 = (a / b)2W2, откуда получаем выражение для контроля вычисления W и V: Wa = Vb.
Легко просматривается связь между  основными элементами эллипсоида:
основными элементами эллипсоида: 
b = a (1- α) = а 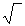 (1-е2) = с(1 – е2), где С полярный радиус кривизны. Очевидно, что (a - b) = αа.
(1-е2) = с(1 – е2), где С полярный радиус кривизны. Очевидно, что (a - b) = αа.
