Математический маятник в постоянном силовом поле
Мы исследовали поведение пружинного маятника в постоянном силовом поле. Зададим тот же вопрос для математического маятника: как изменяется его поведение в постоянном силовом поле?
Попробуем отыскать закономерности в поведении маятника, не вникая в природу постоянного силового поля. Просто в каждой точке траектории на груз кроме силы тяжести действует некая постоянная сила 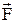 . Будем считать, что нить маятника может свободно вращаться вокруг точки закрепления и, следовательно, занимать любое положение в пространстве.
. Будем считать, что нить маятника может свободно вращаться вокруг точки закрепления и, следовательно, занимать любое положение в пространстве.
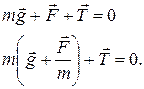 |
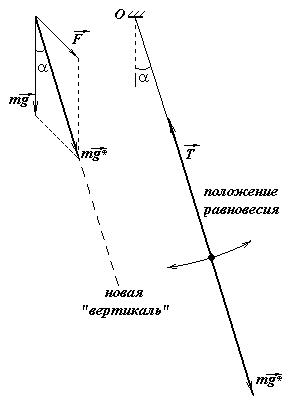
Очевидно, что найдется такое положение, для которого равнодействующая всех приложенных к грузу сил будет равна нулю – это будет положение равновесия.
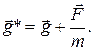 |
В скобках стоит постоянная величина, имеющая размерность ускорения.
Назовем эту величину напряженностью эффективного силового поля.
Тогда,
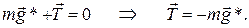
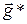 Поскольку сила натяжения нити всегда направлена вдоль нити, в положении равновесия она расположится параллельно вектору напряженности эффективного силового поля . Этот вектор по существу задает положение новой «вертикали», вдоль которой располагается нить маятника в положении равновесия. При выведении из положения равновесия маятник будет колебаться, но теперь уже относительно новой вертикали.
Поскольку сила натяжения нити всегда направлена вдоль нити, в положении равновесия она расположится параллельно вектору напряженности эффективного силового поля . Этот вектор по существу задает положение новой «вертикали», вдоль которой располагается нить маятника в положении равновесия. При выведении из положения равновесия маятник будет колебаться, но теперь уже относительно новой вертикали.
Для нахождения периода колебаний необходимо найти циклическую частоту. Сделать это возможно, получив уравнение гармонических колебаний. Очевидно, что с математической точки зрения мы получили известную задачу, решение которой нами уже найдено ранее. Разница лишь в том, что вместо вектора ускорения свободного падения в выражениях для циклической частоты и периода будет присутствовать вектор напряженности эффективного силового поля.
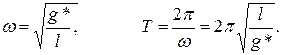 |
Итак, при попадании математического маятника в постоянное силовое поле у него
· изменяется положение равновесия (нить располагается вдоль вектора напряженности эффективного силового поля;
· изменяется период колебаний.
Важно помнить, что роль постоянной силы может играть сила инерции, действующая на маятник в НИСО. В этом случае
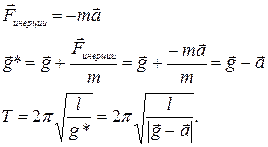 |
§ 3 Примеры решения задач
Задача 1 Математический маятник в невязкой жидкости
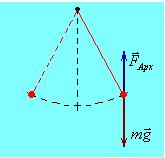 Определите период малых колебаний математического маятника длины L = 20 см, если он находится в жидкости с плотностью в n = 3 раза меньшей плотности материала шарика. Сопротивление жидкости пренебрежимо мало.
Определите период малых колебаний математического маятника длины L = 20 см, если он находится в жидкости с плотностью в n = 3 раза меньшей плотности материала шарика. Сопротивление жидкости пренебрежимо мало.
Решение:
1 Маятник находится в постоянном силовом поле – в каждой точке траектории на него кроме силы тяжести действует выталкивающая сила 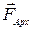 , модуль которой
, модуль которой 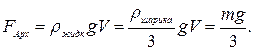
2 Напряженность эффективного силового поля 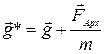 направлена вниз и численно равна
направлена вниз и численно равна 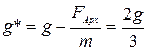 .
.
3 Период колебаний маятника в постоянном силовом поле 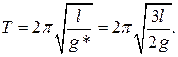
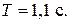
Задача 2 Отставание маятниковых часов
Одно из самых высоких мест на Земле, где живут люди, - монастырь в Гималаях – находится на высоте 5200 м над уровнем моря. На сколько будут отставать за сутки маятниковые часы в этом монастыре, если их выверили на уровне моря? Радиус Земли 6400 км.
Решение:
1 «Правильный» период маятниковых часов на уровне моря 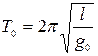 .
.
2 Период часов на высоте 5200 м 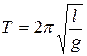 .
.
3 За сутки «неправильные» часы делают 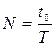 колебаний, где
колебаний, где 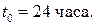 Показания часов после N колебаний будут равны
Показания часов после N колебаний будут равны 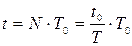 , ибо часы проградуированы в «правильных» периодах.
, ибо часы проградуированы в «правильных» периодах.
4 Отставание часов
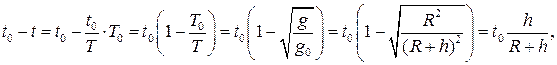
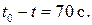
Задача 3 Полная энергия вертикального пружинного маятника
Небольшой шарик, подвешенный на легкой пружине, совершает вертикальные гармонические колебания с амплитудой 2 см. Полная энергия колебаний 0,3 мДж. При каком смещении от положения равновесия на шарик действует возвращающая сила 22,5 мН?
Решение:
1 В процессе колебаний на шарик действуют две силы – тяжести и упругости. Поэтому потенциальная энергия системы будет складываться из потенциальной энергии груза в поле тяготения 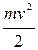 и потенциальной энергии упруго деформированной пружины
и потенциальной энергии упруго деформированной пружины 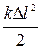 , где
, где 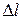 - величина деформации пружины.
- величина деформации пружины.
Полная механическая энергия системы, сохраняющаяся в процессе движения маятника, имеет вид:
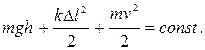
2 Абсолютное значение потенциальной энергии в поле тяготения 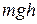 может быть различным – оно зависит от выбора нулевого уровня для отсчета высоты
может быть различным – оно зависит от выбора нулевого уровня для отсчета высоты 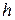 . Соответственно полная механическая энергия системы может принимать любые значения, зависящие от выбора нулевого уровня для отсчета высоты
. Соответственно полная механическая энергия системы может принимать любые значения, зависящие от выбора нулевого уровня для отсчета высоты  . О какой энергии в 0,3 мДж идет речь в задаче?
. О какой энергии в 0,3 мДж идет речь в задаче?
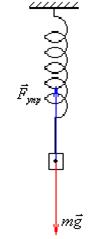 3 В положении равновесия сила упругости уравновешивает силу тяжести
3 В положении равновесия сила упругости уравновешивает силу тяжести
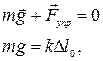
где 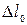 - величина растяжения пружины в положении равновесия.
- величина растяжения пружины в положении равновесия.
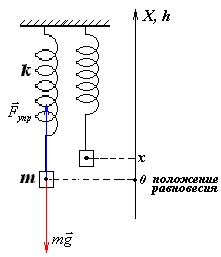 4 Введем систему отсчета, направив координатную ось вертикально вверх. Ноль на оси ОХ поставим в положении равновесия груза. Нулевой уровень для отсчета высоты h тоже выберем в положении равновесия. При таком выборе нулевого уровня координата груза x и высота h будут совпадать x = h.
4 Введем систему отсчета, направив координатную ось вертикально вверх. Ноль на оси ОХ поставим в положении равновесия груза. Нулевой уровень для отсчета высоты h тоже выберем в положении равновесия. При таком выборе нулевого уровня координата груза x и высота h будут совпадать x = h.
5 Выведем маятник из положения равновесия, сместив его в положительном направлении оси ОХ.
Полная механическая энергия системы в этом случае равна:
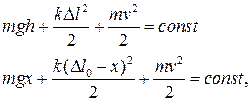
где 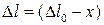 - растяжение пружины в рассматриваемом положении.
- растяжение пружины в рассматриваемом положении.
После преобразований получаем:
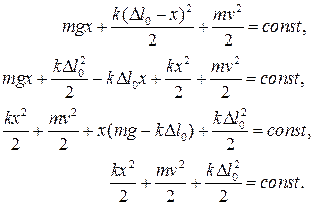
Поскольку величина 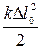 постоянна, то сумма
постоянна, то сумма 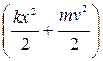 тоже постоянна с течением времени, хотя отдельные ее слагаемые постоянно изменяются.
тоже постоянна с течением времени, хотя отдельные ее слагаемые постоянно изменяются.
Сумму 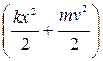 называют энергией колебаний вертикального пружинного маятника. По своему виду эта величина совпадает с полной энергией горизонтального пружинного маятника
называют энергией колебаний вертикального пружинного маятника. По своему виду эта величина совпадает с полной энергией горизонтального пружинного маятника 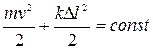 . Однако, если для горизонтального маятника величина
. Однако, если для горизонтального маятника величина 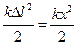 является потенциальной энергией упруго деформированной пружины, то для вертикального маятника величина
является потенциальной энергией упруго деформированной пружины, то для вертикального маятника величина 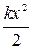 потенциальной энергией пружины уже не является, ибо деформация пружины
потенциальной энергией пружины уже не является, ибо деформация пружины 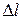 и координата груза х теперь не совпадают
и координата груза х теперь не совпадают 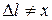 .
.
6 В крайнем положении груз останавливается, следовательно, 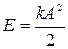 . Находим жесткость пружины
. Находим жесткость пружины 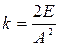 .
.
7 Возвращающая квазиупругая сила имеет вид
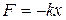 ,
,
где х – координата груза. Тогда координата груза равна 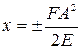 . Два ответа означают, что в двух симметричных относительно положения равновесия точках возвращающая сила по модулю равна 22,5 мН. Их направления, естественно, противоположны.
. Два ответа означают, что в двух симметричных относительно положения равновесия точках возвращающая сила по модулю равна 22,5 мН. Их направления, естественно, противоположны.
х = 1,5 см.
§ 4 Задания для самостоятельного решения
Тест «Маятники в постоянных силовых полях и НИСО»
1 Вертикальный пружинный маятник состоит из груза массы m и пружины жесткостью k. Чему равна деформация пружины в положении равновесия маятника?
А) 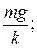 Б)
Б) 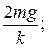 В)
В) 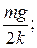 Г) 0.
Г) 0.
2 Груз массы mприкрепили к пружине жесткостью kи удерживают так, чтобы пружина оставалась в недеформированном состоянии. Груз без толчка отпускают. Чему равна амплитуда возникших колебаний?
А) 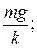 Б)
Б) 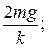 В)
В) 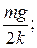 Г) Колебания не возникнут.
Г) Колебания не возникнут.
3 Какой из маятников колеблется с наибольшей частотой?
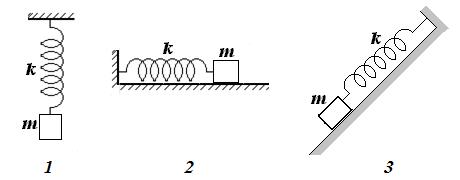
А) 1; Б) 2; В) 3; Г) Частота колебаний всех маятников одинакова.
4 Вертикальный пружинный маятник находится в неподвижном лифте. Как изменится период колебаний маятника, если лифт начнет разгоняться вверх?
А) Увеличится;
Б) Уменьшится;
В) Останется неизменным;
Г) Ответ зависит от величины ускорения, с которым движется лифт.
5 Идеальный пружинный маятник колеблется на горизонтальной гладкой поверхности. Как изменится период колебаний маятника, если поверхность будет шероховатой?
А) Увеличится;
Б) Уменьшится;
В) Останется неизменным;
Г) Ответ зависит от массы груза, жесткости пружины и коэффициента трения
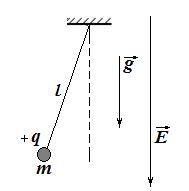 6 Чему равен период колебаний математического маятника, расположенного в вертикальном однородном электрическом поле напряженностью
6 Чему равен период колебаний математического маятника, расположенного в вертикальном однородном электрическом поле напряженностью 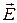 ? Груз маятника заряжен положительно.
? Груз маятника заряжен положительно.
А) 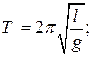 Б)
Б) 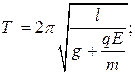 В)
В) 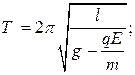 Г)
Г) 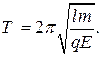
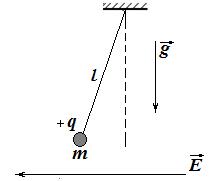 7 Чему равен период колебаний математического маятника, расположенного в однородном горизонтальном электрическом поле напряженностью
7 Чему равен период колебаний математического маятника, расположенного в однородном горизонтальном электрическом поле напряженностью 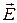 ?
?
А) 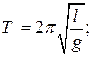 Б)
Б) 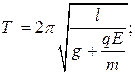 В)
В) 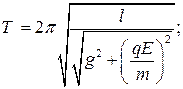 Г)
Г) 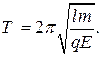
8 Математический маятник находится в лифте. Как рассчитать период колебаний маятника в следующих ситуациях?
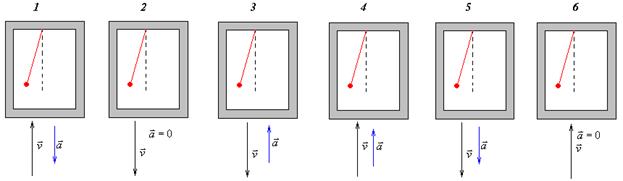
А) 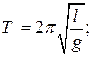 Б)
Б) 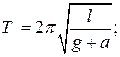 В)
В) 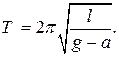
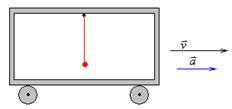 9 Математический маятник длиной l находится в вагоне поезда, разгоняющегося с ускорением
9 Математический маятник длиной l находится в вагоне поезда, разгоняющегося с ускорением 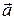 . Как располагается нить маятника в положении равновесия?
. Как располагается нить маятника в положении равновесия?
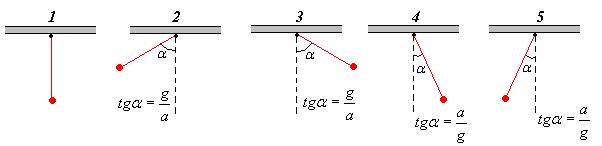
А) 1; Б) 2; В) 3; Г) 4; Д) 5.
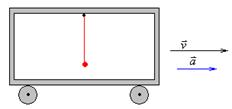 10 Математический маятник длиной l находится в вагоне поезда, разгоняющегося с ускорением
10 Математический маятник длиной l находится в вагоне поезда, разгоняющегося с ускорением 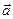 . Чему равен период колебаний маятника?
. Чему равен период колебаний маятника?
А) 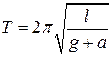 ; Б)
; Б) 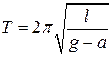 ; В)
; В) 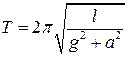 ; Г)
; Г) 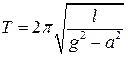 .
.
Задачи
1 Определите период малых колебаний математического маятника длины L = 20 см, если он находится в жидкости с плотностью в n = 3 раза меньшей плотности материала шарика. Сопротивление жидкости пренебрежимо мало.
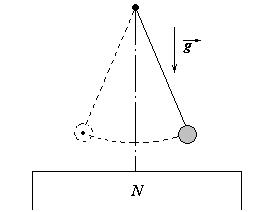 2 Математический маятник – железный шарик массы m, висящий на длинной нити, - имеет период Т0. В присутствии магнита, расположенного чуть ниже шарика, период колебаний стал Т. Определите действующую на шарик магнитную силу.
2 Математический маятник – железный шарик массы m, висящий на длинной нити, - имеет период Т0. В присутствии магнита, расположенного чуть ниже шарика, период колебаний стал Т. Определите действующую на шарик магнитную силу.
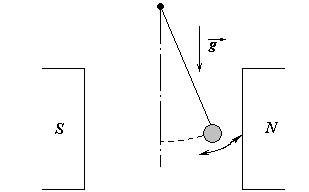 3 Железный шарик маятника поместили между полюсами магнита так, что на него действует горизонтальная магнитная сила. Найдите эту силу и новое положение равновесия шарика, если период его малых колебаний после включения магнитного поля стал равным Т.
3 Железный шарик маятника поместили между полюсами магнита так, что на него действует горизонтальная магнитная сила. Найдите эту силу и новое положение равновесия шарика, если период его малых колебаний после включения магнитного поля стал равным Т.
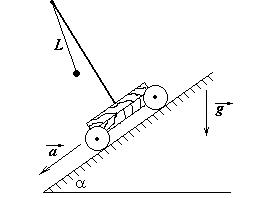 |
4 Тяжелая тележка скатывается с ускорением а с наклонной плоскости, составляющей угол a с горизонтом. Найдите период колебаний маятника длины L, установленного на тележке.
 |
5 Космический корабль вращается вокруг своей оси с угловой скоростью W. Как зависит период колебаний маятника длины L от расстояния R точки подвеса до оси вращения? Плоскость колебаний проходит через ось вращения.
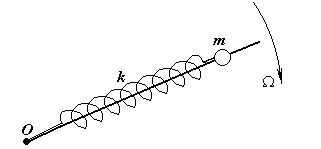
6 Шарик массы m, насаженный на стержень, вращается с угловой скоростью W вокруг оси О, с которой он соединен легкой пружиной жесткости k. Определите частоту колебаний шарика вдоль пружины? Всегда ли возможно колебательное движение?
