Равномерное распределение

Распределение вероятностей непрерывной случайной величины X, принимающей все значения из отрезка [a;b], называется равномерным, если её плотность вероятности на этом отрезке постоянна, а вне его равна нулю. Таким образом, плотность вероятности непрерывной случайной величины X, распределённой равномерно на отрезке [a;b], имеет вид:

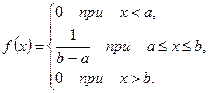
Определим математическое ожидание, дисперсию и среднее квадратическое отклонение для случайной величины с равномерным распределением.

, , .

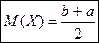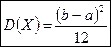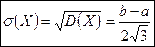Пример. Все значения равномерно распределённой случайной величины лежат на отрезке [2;8]. Найти вероятность попадания случайной величины в промежуток (3;5).

a=2, b=8, .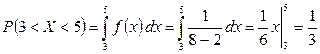

Биномиальное распределение

Пусть производится n испытаний, причём вероятность появления события A в каждом испытании равна p и не зависит от исхода других испытаний (независимые испытания). Так как вероятность наступления события A в одном испытании равна p, то вероятность его ненаступления равна q=1-p.

Пусть событие A наступило в n испытаниях m раз. Это сложное событие можно записать в виде произведения:

.

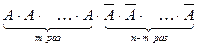Тогда вероятность того, что при n испытаниях событие A наступит m раз 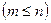, вычисляется по формуле:

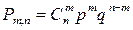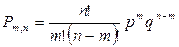или (1)

Формула (1) называется формулой Бернулли.

Пусть X – случайная величина, равная числу появлений события A в n испытаниях, которая принимает значения 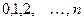с вероятностями:

.

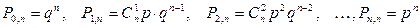Полученный закон распределения случайной величины называется законом биномиального распределения.

X		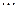		m		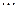n
P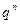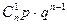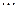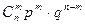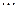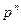

Математическое ожидание, дисперсия и среднее квадратическое отклонение случайных величин, распределённых по биномиальному закону, определяются по формулам:

, , .

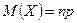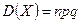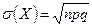Пример. По мишени производятся три выстрела, причём вероятность попадания при каждом выстреле равна 0,8. Рассматривается случайная величина X – число попаданий в мишень. Найти её закон распределения, математическое ожидание, дисперсию и среднее квадратическое отклонение.

p=0,8, q=0,2, n=3, , , .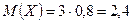

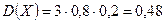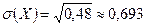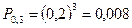- вероятность 0 попаданий;

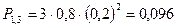- вероятность одного попадания;

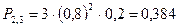- вероятность двух попаданий;

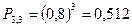- вероятность трёх попаданий.

Получаем закон распределения:

X
P	0,008	0,096	0,384	0,512

Задачи

1. Монету бросают 7 раз. Найти вероятность того, что 4 раза она упадёт гербом вверх.

2. Монету бросают 8 раз. Найти вероятность того, что герб выпадет не более трёх раз.

3. Вероятность попадания в цель при стрельбе из орудия p=0,6. Найти математическое ожидание общего числа попаданий, если будет произведено 10 выстрелов.

4. Найти математическое ожидание числа лотерейных билетов, на которые выпадут выигрыши, если приобретено 20 билетов, причём вероятность выигрыша по одному билету равна 0,3.