Основные уравнения для расчета теплообменников
Тепловой расчет теплообменника может быть конструкторским, целью которого является определение площади поверхности теплообмена, и поверочным, когда при известной поверхности нагрева определяется количество передаваемой теплоты и конечные температуры теплоносителей.
Основными уравнениями для расчета теплообменников являются:
· уравнение теплового баланса;
· уравнение теплопередачи;
· уравнение массового расхода теплоносителей.
Уравнение теплового баланса при условии отсутствия тепловых потерь имеет вид
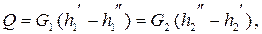 | (9.1) |
где G, кг/с – массовый расход теплоносителя; h, Дж/кг – энтальпия. Здесь и далее индексы 1, 2 относятся соответственно к горячему и холодному теплоносителям, один штрих (¢ ) и два штриха (¢¢ ) – к параметрам на входе в теплообменник и на выходе из него.
При отсутствии кипения или конденсации теплоносителей уравнение теплового баланса можно записать в виде
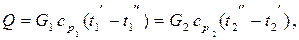 | (9.2) |
где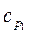 
, 
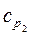, Дж/кг×К – средние теплоемкости теплоносителей,
или
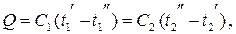 | (9.3) |
где С=G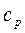 
Дж/с×К – расходная теплоемкость теплоносителя.
Из уравнения (9.3) следует, что отношение расходных теплоемкостей обратно пропорционально отношению их изменений температур:
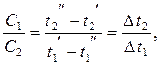 | (9.4) |
Уравнение теплового баланса с учетом тепловых потерь запишется в виде
 |
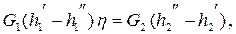где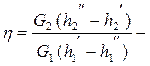 
КПД теплообменника, учитывающий потери тепла в окружающую среду.
Эксергетический КПД теплообменника
 |
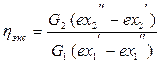учитывает потери эксергии в составе потерь тепла и потери эксергии от необратимого теплообмена между горячим и холодным теплоносителем при конечной разности средних температур (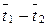 
).
Уравнение теплопередачи имеет вид
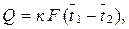 | (9.5) |
где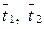 
- средние температуры теплоносителей;
к – коэффициент теплопередачи;
F, м2 – площадь поверхности;
и используется для нахождения площади поверхности теплообмена F.
Если обозначить
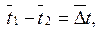 | (9.6) |
где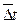 
- средний температурный напор, то уравнение теплопередачи запишется в виде
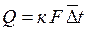 . | (9.7) |
В рекуперативных теплообменниках для уменьшения термического сопротивления стенка выполняется из материала с хорошей теплопроводностью (меди, латуни, сплавов алюминия, стали), и в этом случае для стенок любой формы (например труб) коэффициент теплопередачи с достаточной точностью рассчитывается по формуле для плоской стенки
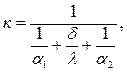 | (9.8) |
где a1, a2, Вт/м2×К – средние коэффициенты теплоотдачи между стенкой и теплоносителями; d, м, l, Вт/м×К – толщина и коэффициент теплопроводности стенки.
В рекуперативных теплообменниках в зависимости от направления потоков горячего и холодного теплоносителей различают три основные схемы движения:
1. Если оба теплоносителя движутся параллельно в одном направлении, то схема называется прямотоком.
2. Если теплоносители движутся параллельно, но в противоположных направлениях, то схема движения называется противотоком.
3. Если один теплоноситель движется в направлении, перпендикулярном к направлению движения другого теплоносителя, то схема движения называется перекрестным током.
Кроме указанных, существуют более сложные схемы движения, являющиеся различными комбинациями рассмотренных основных схем.
 |
На рис. 9.1 представлены графики изменения температур теплоносителей вдоль поверхности теплообмена F для прямотока (а) и противотока (б).
При прямотоке Dt¢=t1¢-t2¢ - температурный напор на входе в теплообменник, Dt¢¢=t1¢¢-t2¢¢ - температурный напор на выходе из теплообменника, Dt – текущий температурный напор при Fх.
Обратите внимание, что при прямотоке температура холодного теплоносителя на выходе теплообменника (t2¢¢) всегда меньше температуры горячего теплоносителя (t1¢¢):
| t2¢¢< t1¢¢. |
При противотоке Dtd , Dtм – больший и меньший температурные напоры. Холодный теплоноситель может нагреваться до более высокой температуры, чем t1¢¢:
| t2¢¢ > t1¢¢. |
Это дает основание заключить, что противоточная схема предпочтительнее прямоточной.
Получим формулу для расчета среднего температурного напора припрямотоке.
Запишем уравнение теплового баланса и уравнение теплопередачи для элемента поверхности dF (рис.9.1,а):
| d Q=-С1dt1=С2 dt2 , | (9.9) |
| d Q=к(t1- t2) dF. | (9.10) |
Из (9.9) имеем
 |
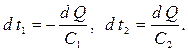Разность
 |
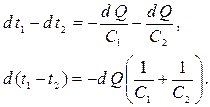Обозначим
 |
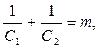тогда
| d (t1- t2)=-т dQ. |
Подставим
 |
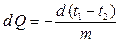в (9.10) и получим
 |
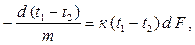откуда
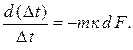 | (9.11) |
Проинтегрируем (9.11) от Dt¢ до текущего температурного напора Dt и от 0 до Fx (рис. 9.1, а), получим
 | |
 | |
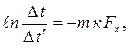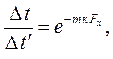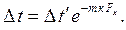 | (9.12) |
Последняя формула описывает закон изменения текущего температурного напора вдоль поверхности теплообмена.
Проинтегрируем (9.11) от Dt¢ до Dt¢¢ и от 0 до F, где F – площадь поверхности теплообменника.
Получим
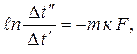 | (9.13) |
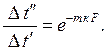 | (9.14) |
Зная закон изменения температурного напора вдоль поверхности теплообмена (9.12), можно найти средний температурный напор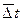 
по формуле осреднения
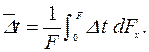 | (9.15) |
Совместное решение (9.15), (9.12) – (9.14) дает расчетную формулу для среднего температурного напора при прямотоке
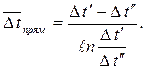 | (9.16) |
При противотоке
 |
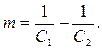Аналогичные рассуждения и математические преобразования дают расчетную формулу для 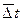в виде
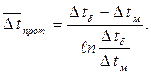 | (9.17) |
Учитывая, что для прямотока Δt¢ является бóльшим температурным напором, а Δt¢¢ - меньшим, можно утверждать, что формула (9.17) справедлива и для прямотока.
Для других схем движения теплоносителей средний температурный напор рассчитывается по формуле
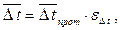 | (9.18) |
где eDt=f (R, P) – поправочный коэффициент, определяемый по номограммам, которые приведены в справочниках.
Здесь
 |
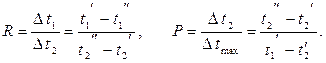Расчет средних температур теплоносителе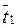й 
и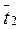 
производится так: сравнивают изменения температур Dt1=t1¢-t2¢¢ и Dt2= t2¢¢-t2¢ ; среднюю температуру теплоносителя с меньшим изменением температуры (с бóльшей расходной теплоемкостью) вычисляют как среднюю арифметическую. Среднюю температуру другого теплоносителя определяют по формуле (9.6).
Уравнение массового расхода теплоносителя имеет вид
| G=w f r, кг/с, | (9.19) |
где w, м/с – скорость движения теплоносителя,
f, м2 – площадь поперечного сечения потока теплоносителя,
r, кг/м3 – плотность теплоносителя.
При движении теплоносителя по трубам пучка площадь поперечного сечения всех труб
 |
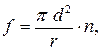где п – число труб.