Сходимость градиентного метода

Сходимость метода гарантируется при выборе начального приближения вблизи .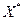

В любом случае метод может остановитья в точке относительного метода.

Численное решение обыкновенных дифференциальных уравнений

Обыкновенные дифференциальные уравнения (ОДУ) встречаются при описании движения системы взаимодействующих материальных носителей (механике, химической кинетике, электрических цепях, сопротивлении материалов и многих других явлениях жизни).Ряд важнейших задач сводится к задачам с обыкновенными дифференциальными уравнениями, а именно теория автоматического управления базируется на ОДУ, а также и другие курсы специальности АЭП

Простейшим ОДУ является уравнение 1-го порядка:

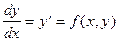
ОДУ n-го порядка имеет вид:

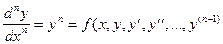
Однако любое уравнение n-го порядка можно свести к системе из n уравнений 1-го порядка:

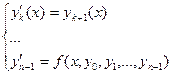
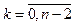
или

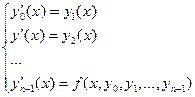
Таким образом, решение дифференциального уравнения n-го порядка сводится к решению системы дифференциальных уравнений 1-го порядка (количество дифференциальных уравнений в системе = n).

Если ввести следующие обозначения:

,

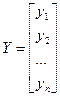
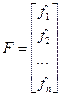то систему дифференциальных уравнений можно переписать в векторно-матричном виде:

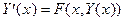(1)

Известно, что система n-го порядка имеет множество решений,, которые в общем случае зависят от постоянных С, общее количество которых -n. Общее решение системы ОДУ может быть записано в ви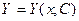де:

,где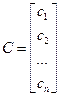

Для определения значения этих параметров, т.е. выделения единственного решения необходимо учитывать дополнительные условия. В зависимости от выбора дополнительных условий определены следующие типы задач для обыкновенных дифференциальных уравнений:

- задача Коши;

- краевая задача;

- задача на собственные значения.

Задача Коши.

Задача Коши, или задача с начальными условиями, имеет следующие дополнительные условия:

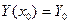
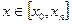
Краевая задача.

Когда дополнительные условия заданы как в точке 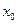, так и в точке .

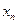Задача на собственные значения.

Если функция 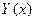зависит от параметров :

,

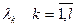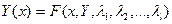где .

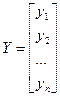
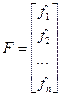Число дополнительных условий должно быть соответственно 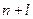. Функции 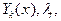где 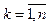; 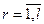удовлетворяющее всем уравнениям, называются собственными дифференциальными или собственными значениями задачи.

Методы решения ОДУ.

Обыкновенные дифференциальные уравнения могут быть решены следующими методами:

1. аналитическими;
2. численными;
3. графическими;
4. приближенными.

Аналитические методы дают решение в виде аналитического выражения.

Графические методы дают приближенное решение в виде графика.

Численные методы дают частное решение для определенных 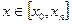в виде таблицы, Численные методы применяются только к корректно поставленным задачам, т.е. к таким, у которых малое изменение начальных значений, приводит к малому изменению интегральных кривых.

Пример.

Пусть дано следующее ОДУ:

.

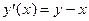Необходимо решить задачу Коши для .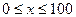

Начальные условия имеют вид:

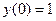
Общее решение имеет вид:

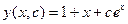
при 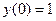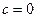решение .

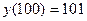Однако при малом изменении начальных условий:

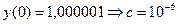решение в точке 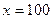: 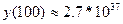. То есть имеет место плохо обусловленная задача.