Комбінаторика, теорія ймовірностей
Формули скороченого
Множення
(а−в)(а+в) = а2−в2
(а+в)2 = а2+2ав+в2
(а−в)2 = а2−2ав+в2
(а+в)3 = а3+3а2в+3ав2+в3
(а−в)3 = а3−3а2в+3ав2−в3
Розкладання на множники
а2−в2 =(а−в)(а+в)
а3+в3 = (а+в)(а2−ав+в2)
а3−в3 = (а−в)(а2+ав+в2)
ах2+вх+с = а(х−х1)(х−х2)
Формула коренів квадратного рівняння ах2+вх+с = 0
D = в2−4ас
х1,2 = 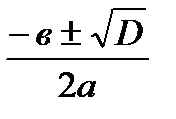
Теорема Вієта
х2+рх+q = 0
х1+х2 = − р
х1·х2 = q
Координати вершини параболи
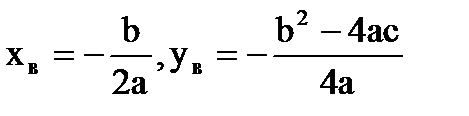
Арифметична прогресія
d = a2−a1 або d = an+1−an
an = a1+ (n−1) d
an = 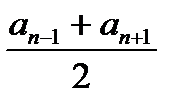
Sn = 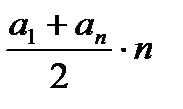
Sn = 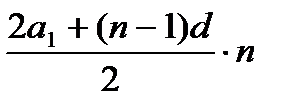
Геометрична прогресія
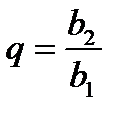 або
або 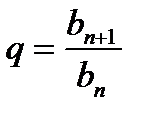
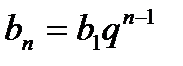
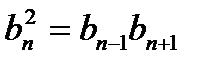
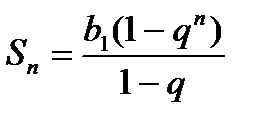
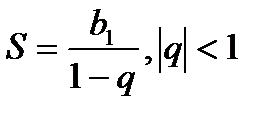 − сума нескінчен. геом. прогресії
− сума нескінчен. геом. прогресії
Властивості степенів
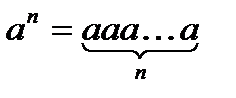
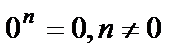
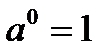 ;
; 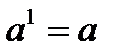 ;
; 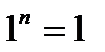

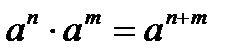
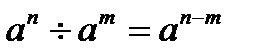
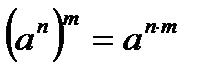
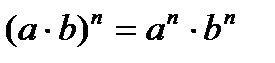
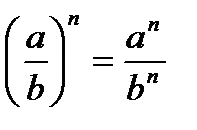
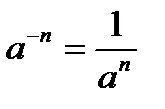 ;
; 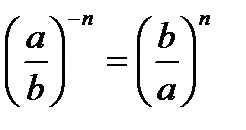
Властивості квадратних коренів
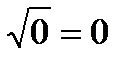 ;
; 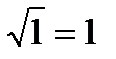
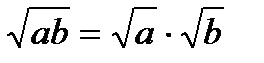
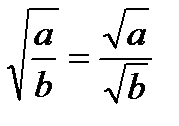
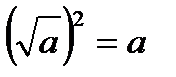 ;
; 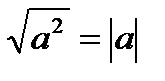
Властивості коренів n−го степеня
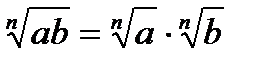
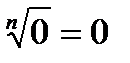
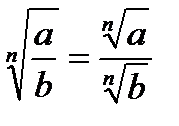
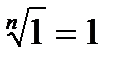
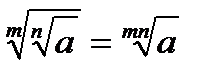
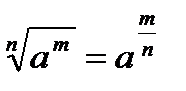
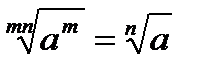
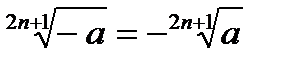
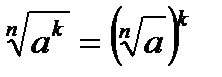
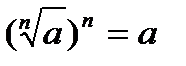
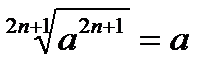
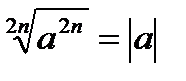
Властивості логарифмів
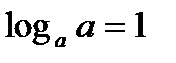 ;
; 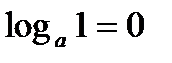
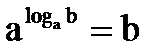 ;
; 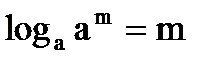
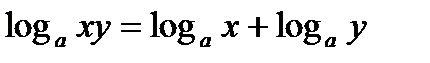
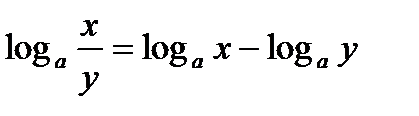
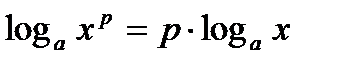
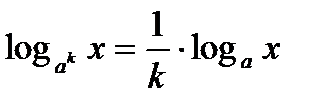
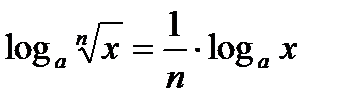
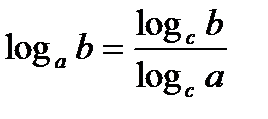 ;
; 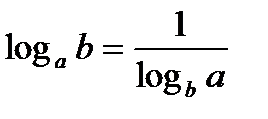
Похідна
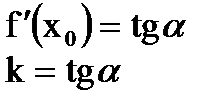
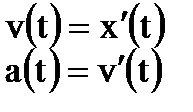
Рівняння дотичної:
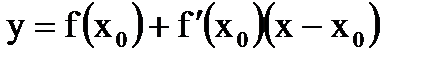
Похідні деяких функцій
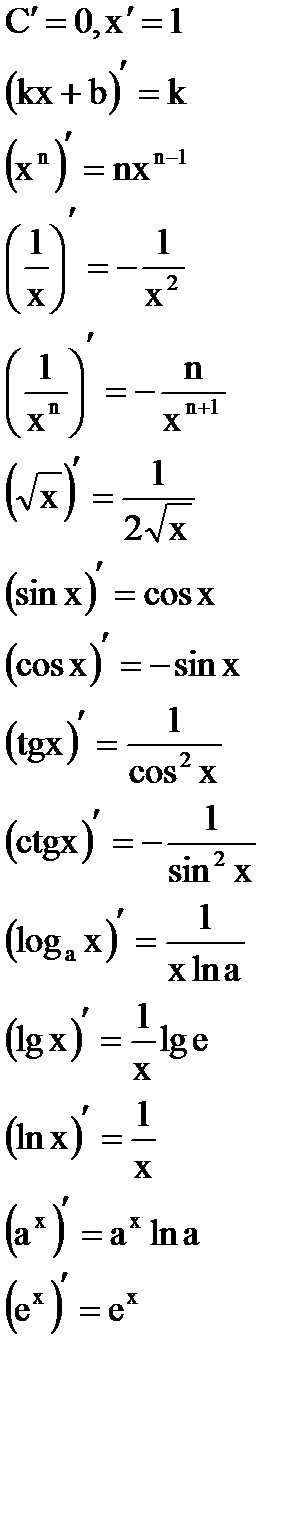
Правила диференціювання
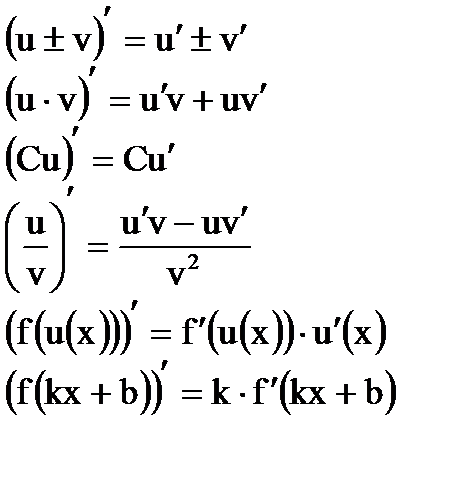
Інтеграли деяких функцій
(таблиця первісних)
| f(x) | F(x)+C = ∫ f(x) dx |
| k | kx + C |
| xn | 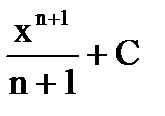 |
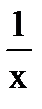 | ln |x| + C |
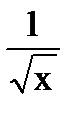 | 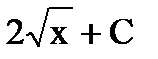 |
| sin x | -cos x + C |
| cos x | sin x + C |
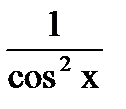 | tg x + C |
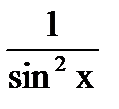 | -ctg x + C |
| ax | 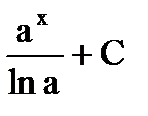 |
| ex | ex + C |
| tg x | −ln |cos x| + C |
| ctg x | ln |sin x| + C |
Правила інтегрування
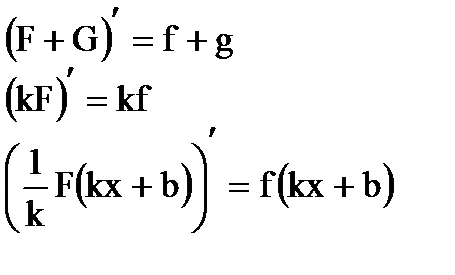
Формула Ньютона-Лейбниця
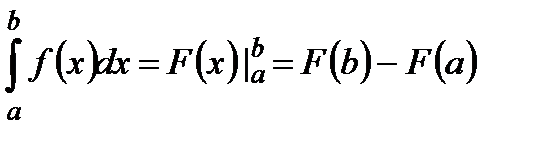
Площа криволінійної трапеції
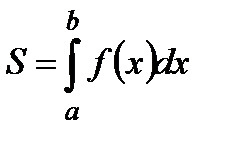
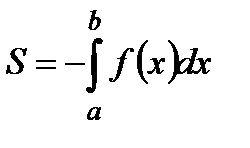
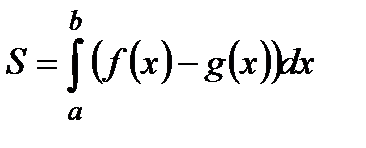


Об’єм тіла обертання
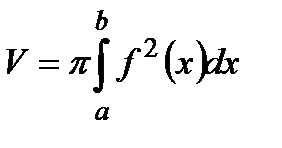
Деякі значення триг. функцій
| α | 0° | 30° | 45° | 60° | 90° | 180° |
| π/6 | π/4 | π/3 | π/2 | π | ||
| sin α | 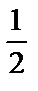 | 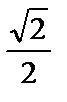 | 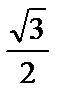 | |||
| cos α | 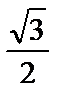 | 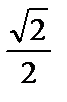 | 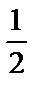 | −1 | ||
| tg α | 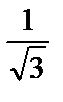 | 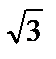 | − | |||
| ctg α | − | 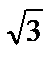 | 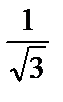 | − |
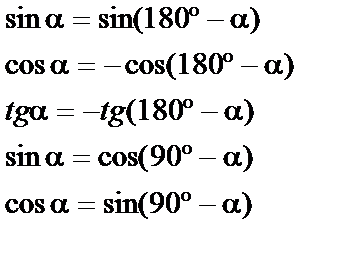
Періодичність
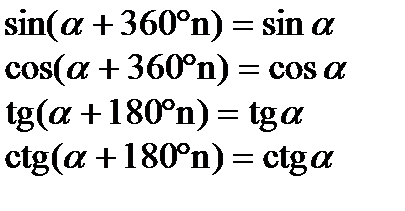
Парність
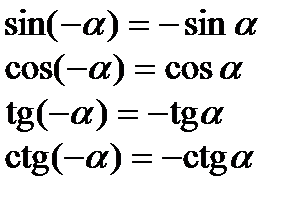
Знаки триг. функцій
| + |
| + |
| - |
| - |
| + |
| + |
| + |
| + |
| -_ |
| - |
| - |
| - |
sin α cos α tg α, ctg α
Співвідношення між триг. функціями одного і того
Самого аргументу
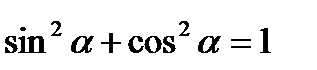
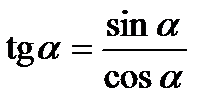
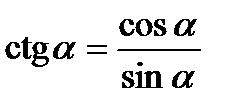
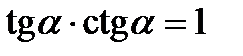
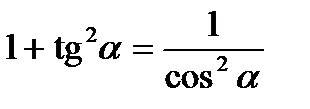
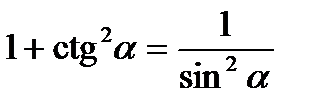
Формули подвійного аргументу
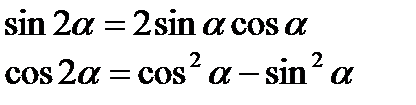

Формули додавання
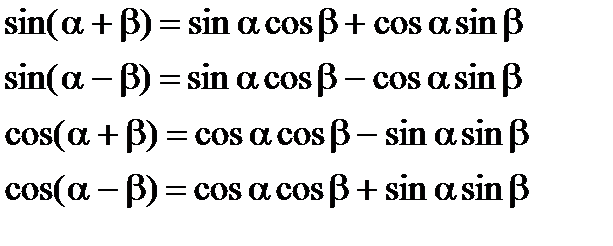
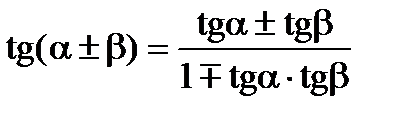
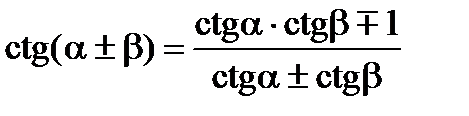
Формули перетворення суми і різниці триг. функцій у добуток
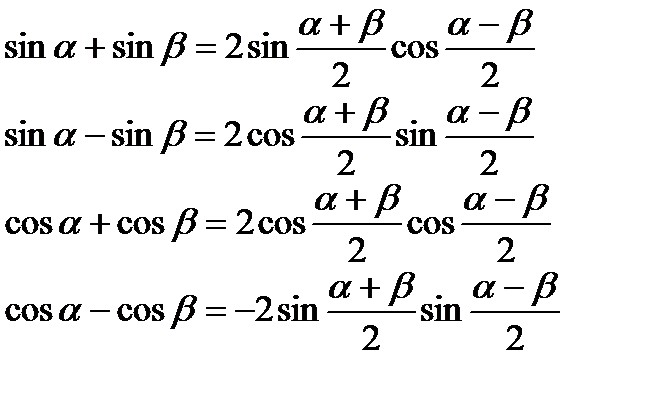
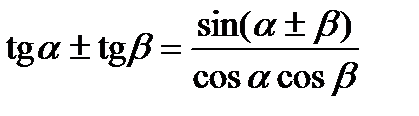
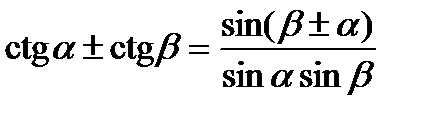
Формули половинного аргументу та зниження степеня
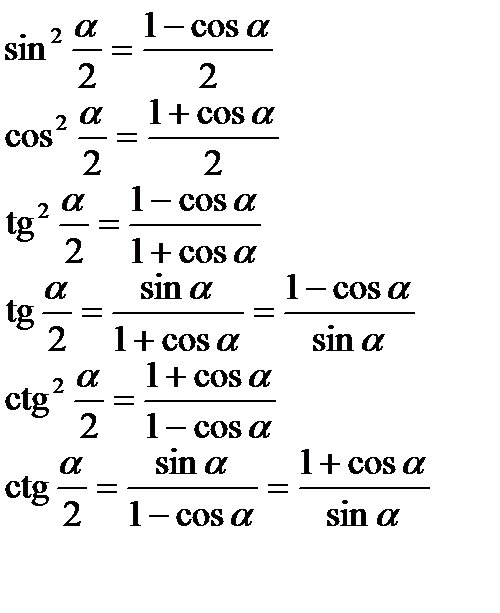
Формули перетворення
добутку триг. функцій у суму 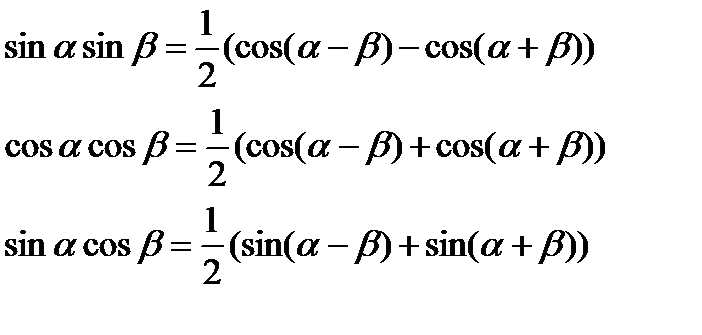
Обернені триг. функції
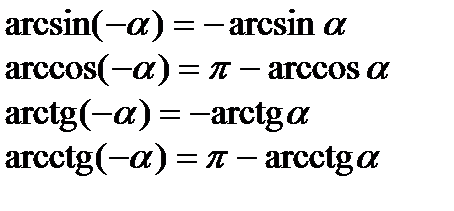
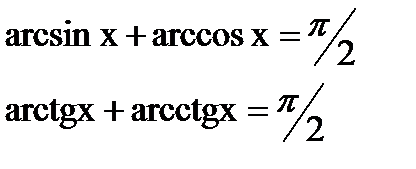
Найпростіші триг. рівняння
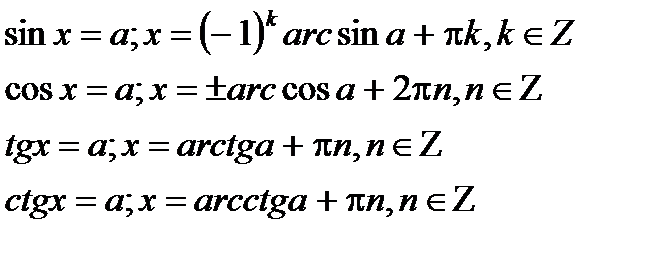 Окремі випадки
Окремі випадки
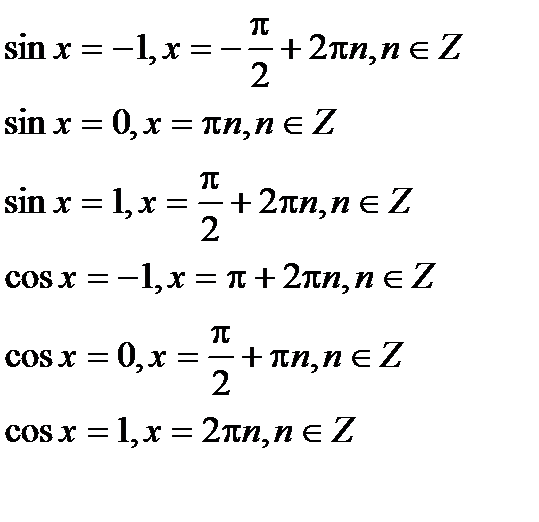
Триг. функції в прямокутному
трикутнику
a c 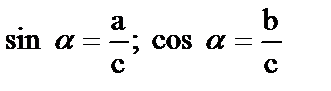
b α 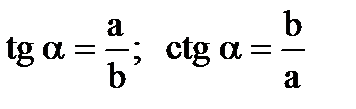
Катет дорівнює добутку гіпотенузи на sin протилежного кута або на cos кута між ними.
Гіпотенуза дорівнює: катет поділити на sin протилежного кута або на cos прилеглого кута (кута між ними).
Довільний трикутник
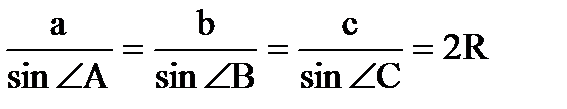
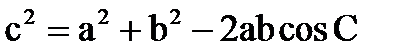
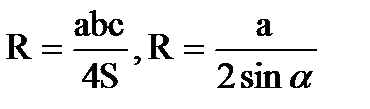
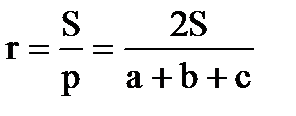
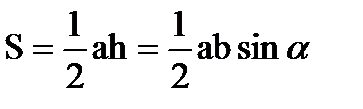
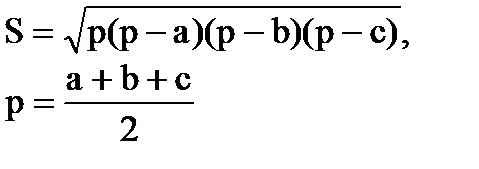
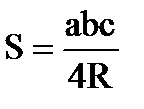 b α h с
b α h с
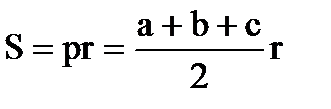
Властивість медіан
B
D
O
A C
AO:OD = 2:1
Властивість бісектрис
B
A D C
AB:AD=BC:DС, AB:BC=AD:DС
Прямокутний трикутник
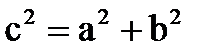 a c
a c
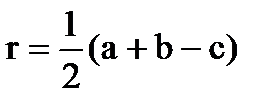 R b
R b
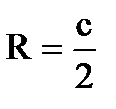 ,
, 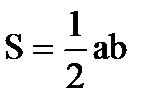
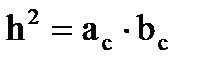
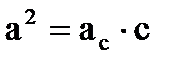 a h b
a h b 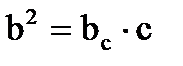 ac bc
ac bc
Рівносторонній трикутник
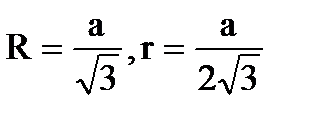 ,
, 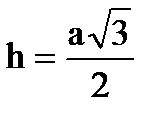
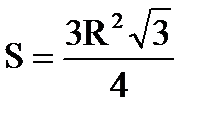
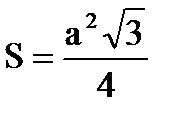 a h a
a h a
а
Опуклий чотирикутник
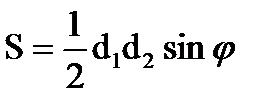
d1 φ d2
Паралелограм
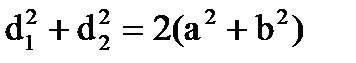 d1 d2
d1 d2
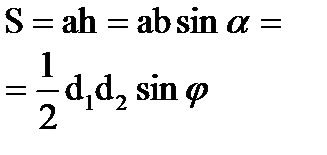 b h φ
b h φ
α a
Ромб
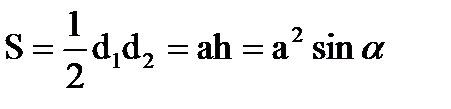
a a
d1 h
α d2
а
Прямокутник
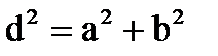 d d
d d
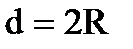 b φ b
b φ b
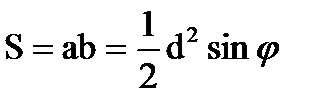 a
a
Квадрат
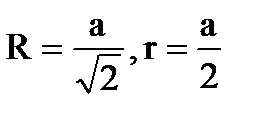
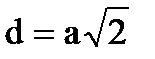 a
a
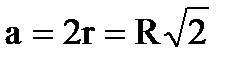 a d
a d
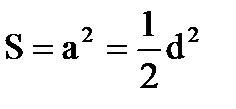
Шестикутник
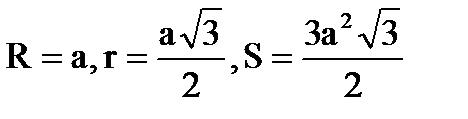
Трапеція
| ℓ |
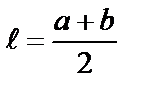 B a C
B a C 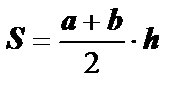 А b h D
А b h D
Якщо в трапецію можна вписати коло, то сума її бічних сторін дорівнює сумі її основ: АВ+СD=ВС+АD.
Якщо трапеція вписана в коло, то вона рівнобічна.
| Призма | Піраміда |
| Sбіч = Росн∙Н Sповн=Sбіч+2Sосн V = Sосн∙H | Sбіч(прав)= 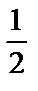 Росн∙ℓ Sповн = Sбіч + Sосн V = Росн∙ℓ Sповн = Sбіч + Sосн V = 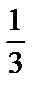 Sосн∙H Sосн∙H |
| Циліндр | Конус |
| Sбіч = 2πRН Sповн=Sбіч+2Sосн Sосн = πR2 V=Sосн∙H=πR2H | Sбіч = πRℓ Sповн = Sбіч + Sосн Sосн = πR2 V= 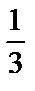 Sосн∙H= Sосн∙H= 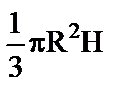 |
| Куля (сфера) | |
| Sпов = 4πR2 | 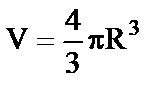 |
Якщо в рівнобічній трапеції діагоналі перпендикулярні, то її висота співпадає з середньою лінією.
Коло
C = 2πR, d = 2R
S = πR2, S = πd2/4
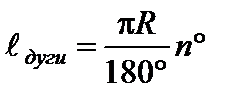 E P L
E P L
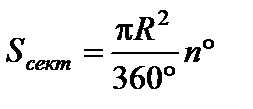 K R n˚ F
K R n˚ F
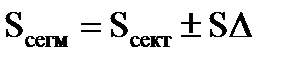
ЕР∙РF = KP∙PL P
F
FP2=BP∙AP A M
BP∙AP=NP∙MP
B
N
В
| С |
| D |
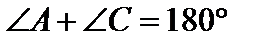
| А |
| В |
| С |
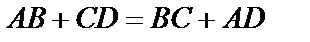
| D |
| А |
| В |
| А |
| О |
| С |
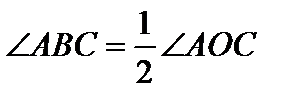
Вписаний кут дорівнює половині центрального кута, що спирається на ту саму дугу.
Вписані кути, які спираються на одну і ту саму дугу (хорду), рівні між собою.
Вписаний кут, який спирається на діаметр, дорівнює 90°.
Декартові координати
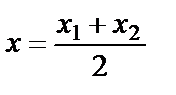 ;
; 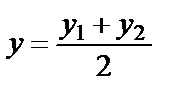 – координати середини відрізка
– координати середини відрізка
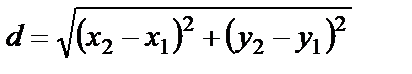 – відстань між двома точками
– відстань між двома точками
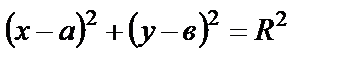 – рівняння кола з центром в точці (а; в) і радіусом R
– рівняння кола з центром в точці (а; в) і радіусом R
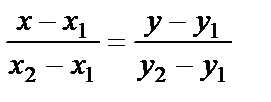 – рівняння прямої
– рівняння прямої
Вектори
А(х1; у1) В(х2; у2), 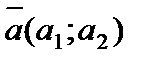
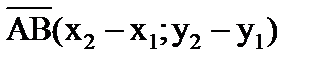 –координати в-ра
–координати в-ра
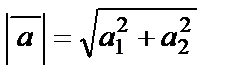 – модуль вектора
– модуль вектора
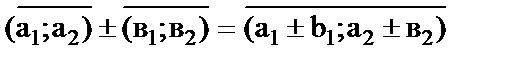
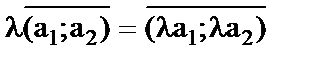
Якщо 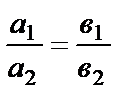 ,то вектори колінеарні.
,то вектори колінеарні.
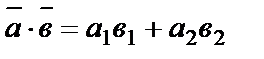 – скалярний добуток
– скалярний добуток 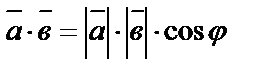 –скалярний добуток
–скалярний добуток 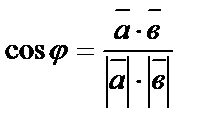 –кут між векторами
–кут між векторами 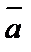 і
і 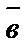
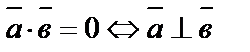
Комбінаторика, теорія ймовірностей
Розміщення(не всі елементи, важливий порядок)
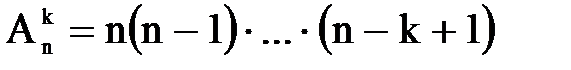
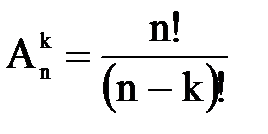
Перестановки(використовуються всі елементи)
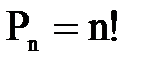
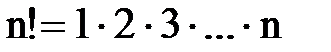
Сполучення(не всі елементи, порядок елементів не важливий)
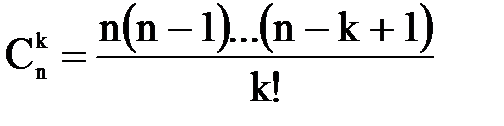
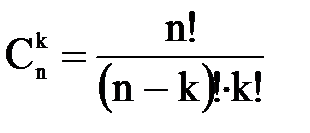
Біном Ньютона
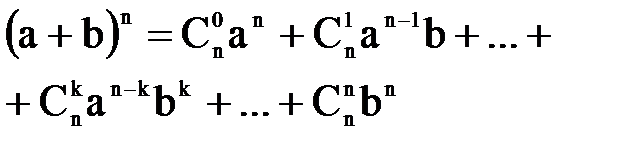
Імовірність подій
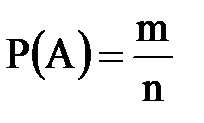 ,
,
де n − число всіх можливих випадків події А, а m − число сприятливих наслідків цієї ж події А
