Математическая модель задачи

X_ij — объемы перевозок с i-ой фабрики-производителя в j-ый центр распределения;

С_ij — стоимости перевозки ед. продукции с i-ой фабрики в j-ый центр распределения.

Необходимо минимизировать целевую функцию (транспортные расходы)

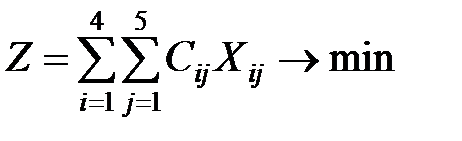
при следующих ограничениях:

1) объем перевозок со всех фабрик в j центр распределения равен спросу в j центре распределения: ;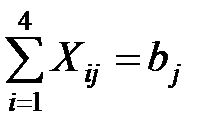

2) объем перевозок с i фабрики во все центры распределения равен объему производства на i фабрике: ;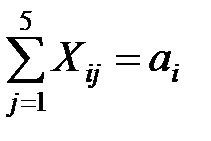

3)объемы перевозок положительны: .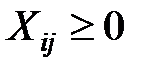

Решение задачи в Excel

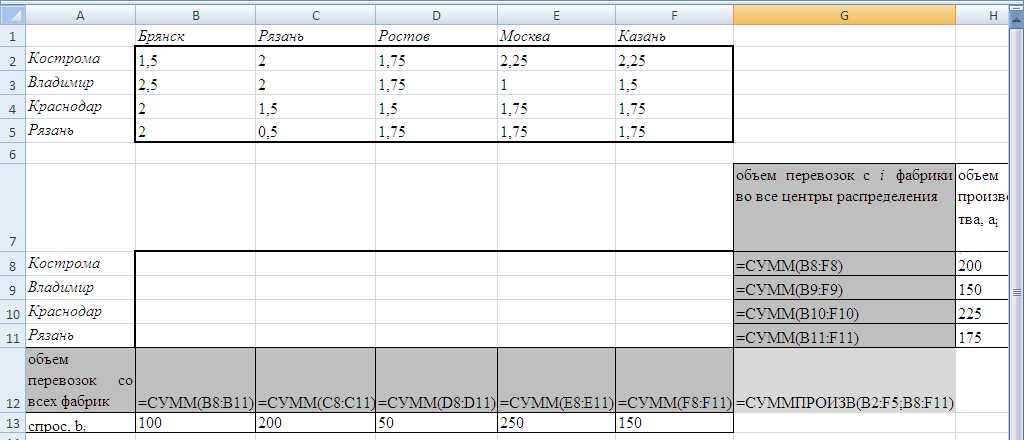
В ячейки B2:F5 ввести стоимости перевозок, B8:F11 — объемы перевозок (неизвестны), H8:H11 — объемы производства на фабриках, B13:F13 – потребность продукции в пунктах потребления,

В ячейку G12 ввести целевую функцию

= СУММПРОИЗВ(B2:F5;B8:F11), В ячейки B12,..,F12 ввести =СУММ(B8:B11) и т.д., В ячейки G8,..,G11 ввести =СУММ(B8:F8) и т.д.

Вид листа в Excel:

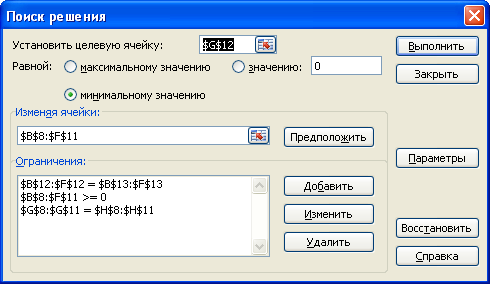
Выполнить команду Данные / Поиск решения

Заполнить диалоговое окно в соответствии с условиями модели. Установить в параметрах Поиска решенияфлажок Линейная модель.

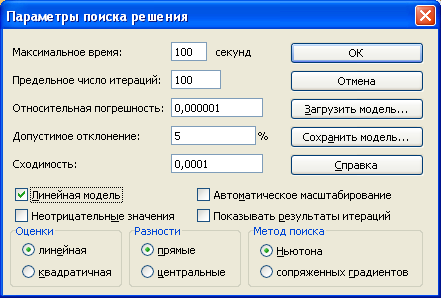
Нажмите кнопку Выполнить.

Ответ:

						объем перевозок с i фабрикиво все центры распределения	объем производства, ai
Кострома							200
Владимир
Краснодар
Рязань
объем перевозок со всех фабрик
спрос, bj

Задание 2. Решить транспортную задачу

Вариант 1

Груз, хранящийся на четырех складах С1 (С1 – склад 1), С2, С3, С4, необходимо развести по 6-ти магазинам М1 (М1 – магазин 1), М2, М3, М4, М5, М6. Для перевозки грузов требуется 45,40,45,50 автомашин соответственно. Первому магазину требуется 24 машин груза, второму – 32, третьему – 18, четвертому -17, пятому – 22 и шестому – 27 машин. Стоимость пробега одной автомашины за 1 км составляет 7 ден. ед. Составьте оптимальный по стоимости план перевозки грузов со складов до магазинов. Расстояния от складов до магазинов указаны в следующей таблице.

	М1	М2	М3	М4	М5	М6
С1
С2
С3
С4

Вариант 2

На четырех элеваторах ЭA (ЭA — Элеватор А), ЭB, ЭC, ЭD находится зерно в количестве 110, 125, 145, 135 т, которое нужно доставить на четыре сельскохозяйственных предприятия для посева. Предприятию 1 необходимо поставить 135т, предприятию 2 — 145, предприятию 3 — 80, предприятию 4 — 155т зерна. Составьте оптимальный план перевозки зерна из условия минимума стоимости перевозки. Стоимость доставки потребителям от поставщиков представлена в таблице.

	П1	П2	П3	П4
ЭA
ЭB
ЭC
ЭD

Вариант 3

Завод выпускает продукцию в четырех цехах: ЦA (ЦA — Цех А), ЦB, ЦC, ЦD расположенных на разных территориях. Свою продукцию завод поставляет в пять магазинов города. Цех A производит 125 тыс. изделий, цех B — 105, цех С — 95 и цех D — соответственно 130 тыс. шт. изделий. Плановая потребность магазинов в продукции завода следующая: М1 – 110 тыс. шт. изделий, М2 — 70 тыс. шт., М3 — 45 тыс. шт., М4 — 75 тыс. шт., и М5 — 115 тыс. шт. Составьте такой план перевозки изделий, при котором расходы на перевозку изделий были бы наименьшими. Стоимость перевозки 1 тыс. шт. изделий из цехов в магазины приведена в таблице

.

	М1	М2	М3	М4	М5
ЦA
ЦB
ЦC
ЦD

Вариант 4

Имеются четыре овощехранилища О1 (О1 — Овощехранилище 1), О2, О3, О4, расположенные в разных районах города, в которых сосредоточено 15, 25, 45 и 40 т овощей соответственно. Овощи необходимо перевезти четырем потребителям П1, П2, П3, П4 соответственно в количестве 35, 25, 45 и 15 т. Затраты на перевозку 1т овощей на 1 км постоянны и равны 25 руб. Определите план перевозок продукта от хранилищ до потребителей из условия минимизации транспортных расходов. Расстояния от овощехранилищ до потребителей следующие:

	П1	П2	П3	П4
О1
О2
О3
О4

Вариант 5

Торговая фирма «Весна и осень» включает четыре предприятия П1 (П1 — предприятие 1), П2, П3, П4 и шесть складов С1 (С1 — склад 1), С2, С3, С4, С5, С6 в различных регионах страны. Каждый месяц предприятия фирмы производят 100, 15, 90 и 55 ед. продукции. Вся производимая продукция направляется на склады, вместимость которых следующая: 30, 40, 55, 80, 45, и 10 ед. продукции. Определите план перевозок из условия минимизации ежемесячных расходов на транспортировку. Издержки транспортировки продукции от предприятий до складов следующие (ден. ед.):

	С1	С2	С3	С4	С5	С6
П1
П2
П3
П4

Вариант 6

Четыре хлебных комбината К1 (К1 — комбинат 1), К2, К3, К4 с производственными мощностями 115, 125, 90, 120 т хлебобулочных изделий в сутки поставляет свою продукцию в 5 магазинов города М1 (М1 — магазин 1), М2, М3, М4, М5. Потребность в хлебобулочных изделиях магазинов следующая: 80, 95, 75, 110, 90 т. Определите план перевозок из условия минимизации ежедневных расходов на транспортировку. Издержки транспортировки продукции от хлебных комбинатов до магазинов следующие (ден. ед):

	М1	М2	М3	М4	М5
К1
К2
К3
К4

Варианты 7–12. Условие

С трёх складов, расположенных в Химках, на Сходне и в Ховрино, необходимо доставить в пять магазинов сахарный песок в соответствии с заявкой каждого магазина. Объёмы запасов песка, имеющегося на складах, объёмы заявок магазинов и тарифы на поставку одной тонны груза со складов в магазины даны в таблице.

Вариант 7

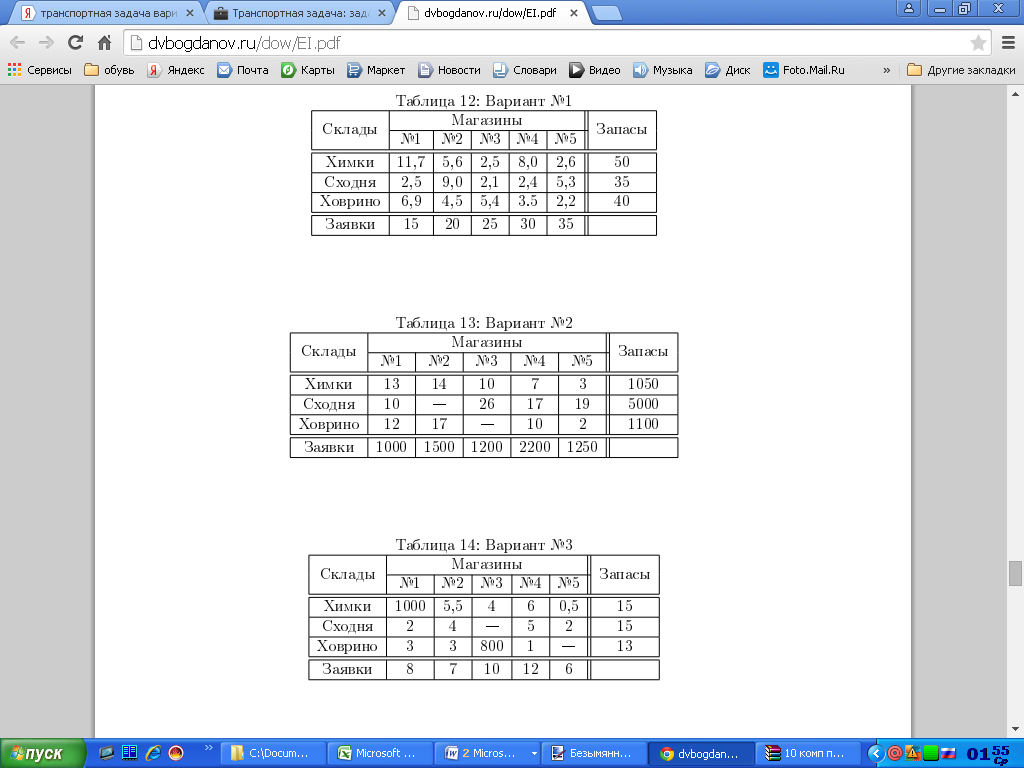
Вариант 8

Вариант 9

Вариант 10

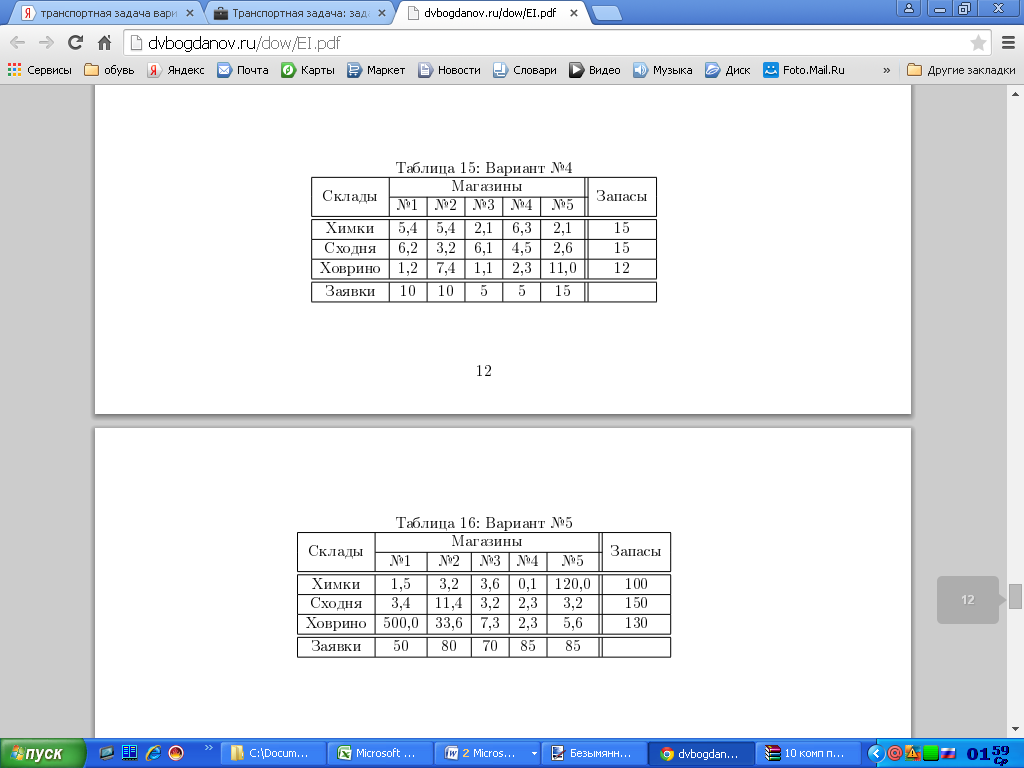
Вариант 11

Вариант 12

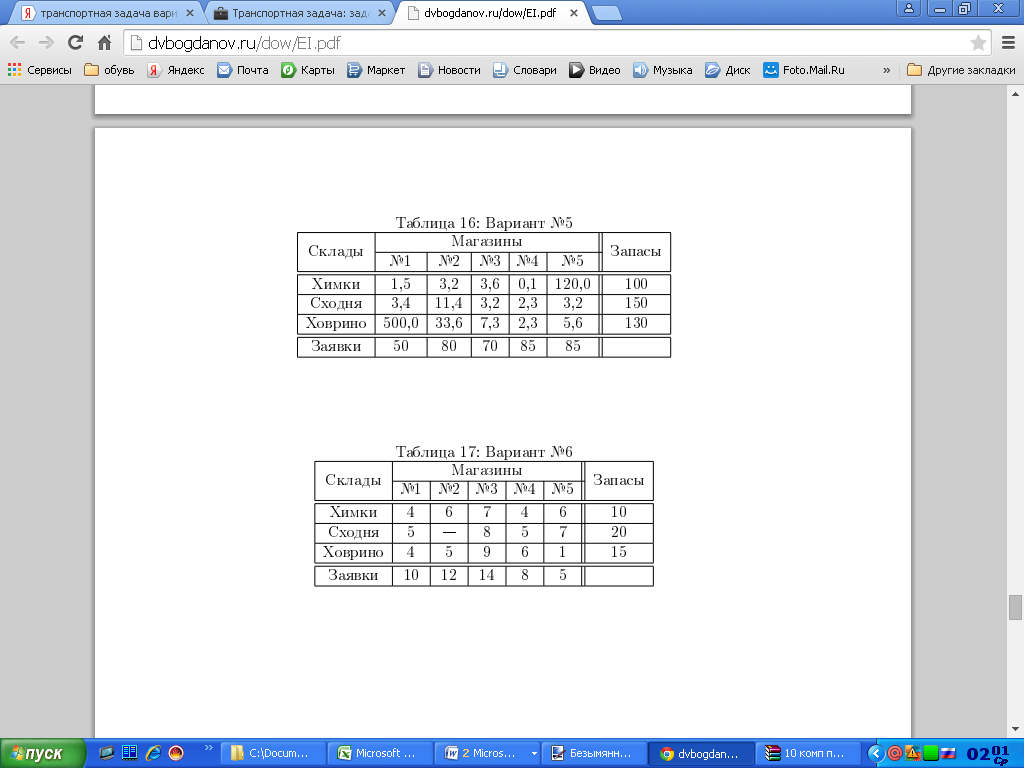
Вариант 13

Три склада (A1:A3) поставляют в три магазина (B1:B3) розничной сети некоторый товар. Запасы данного товара на складах (шт.), потребности в нем магазинов (шт.)и тарифы на перевозку (в расчете на 1 шт.) показаны в транспортной таблице ниже. Найдите оптимальный план грузоперевозок, обеспечивающий удовлетворение потребностей магазинов в товаре с минимальными издержками на его транспортировку.

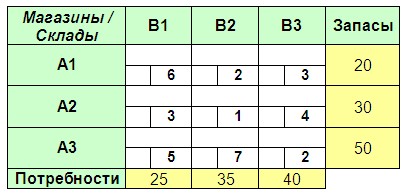
Вариант 14

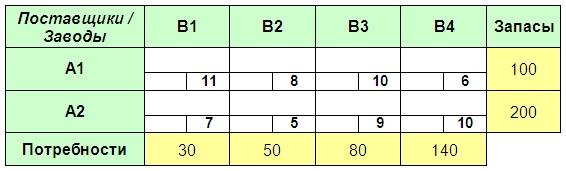
Два поставщика (A1:A2) обеспечивают четыре завода (B1:B4) необходимым для производства продукции сырьем. Запасы сырья на складах поставщиков (т.), потребности в нем заводов (т.) и тарифы на перевозку (в расчете на 1 т.) приведены в транспортной таблице ниже. Найдите оптимальный план грузоперевозок, обеспечивающий удовлетворение потребностей заводов в сырье с минимальными издержками на его транспортировку.

Вариант 15

Груз, хранящийся на четырех складах С1 (С1 — склад 1), С2, С3, С4, необходимо развести по 6-ти магазинам М1 (М1 — магазин 1), М2, М3, М4, М5, М6. Для перевозки грузов требуется 45,40,45,50 автомашин соответственно. Первому магазину требуется 24 машин груза, второму — 32, третьему — 18, четвертому — 17, пятому — 22 и шестому — 27 машин. Стоимость пробега одной автомашины за 1 км составляет 7 ден. ед. Составьте оптимальный по стоимости план перевозки грузов со складов до магазинов. Расстояния от складов до магазинов указаны в следующей таблице.

	М1	М2	М3	М4	М5	М6
С1
С2
С3
С4

Вариант 16

С трёх складов, расположенных в Химках, на Сходне и в Ховрино, необходимо доставить в пять магазинов сахарный песок в соответствии с заявкой каждого магазина. Объёмы запасов песка, имеющегося на складах, объёмы заявок магазинов и тарифы на поставку одной тонны груза со складов в магазины даны в таблице.

Задача коммивояжера

Имеется n городов. Выезжая из исходного города А₁, коммивояжер должен побывать во всех остальных городах по одному разу и вернуться в город А₁. Задача заключается в определении последовательности объезда городов, при которой коммивояжеру требуется минимизировать некоторый критерий эффективности — стоимость проезда, время в пути, суммарное расстояние и т.д.

Математическая модель

Пусть задана матрица T=||t_ij||, в которой задано время, затрачиваемое на переезд между городами, и требуется минимизировать время в пути.

Введем булевы переменные:

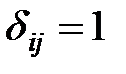, если коммивояжер переезжает из города А_i в город А_j, i ≠ j;

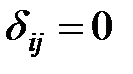, в противном случае, .

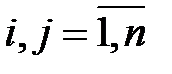Целевая функция имеет вид: .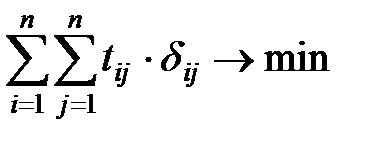

ЦФ представляет собой суммарное время в пути.

Ограничения имеют вид:

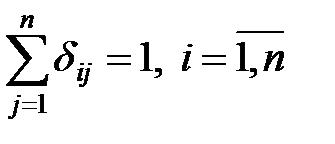, (1)

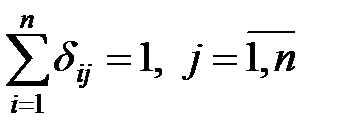, (2)

Так как нельзя непосредственно возвращаться из города i в город i, то .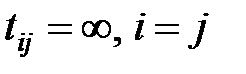

Исключение подциклов длины меньшей n задается условием

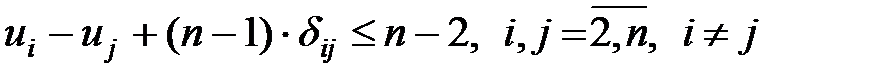, (3)

где 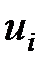— неограниченные действительные переменные.

Условия (1) означают, что коммивояжер выезжает из каждого города один раз, а условия (2) — что он въезжает один раз в каждый город. Условия (3) предназначены обеспечить связность маршрута коммивояжера. Более точно, эти условия запрещают любой цикл, не проходящий через город 1, и тем самым исключают ситуации, подобные приведенной на рисунке.

Решение в Excel

Коммивояжеру, находящемуся в Париже, необходимо посетить три города. Он получил информацию о стоимости проезда самолетом в каждый из выбранных городов и стоимость проезда из одного города в другой. На основе добытых данных он составил матрицу стоимостей (см. табл.) проезда в выбранные города и обратно. Зная матрицу стоимостей коммивояжеру надо так составить маршрут путешествия, чтобы затраты на путешествие были бы минимальными и чтобы выполнялось требование: каждый пункт посещается только один раз.

Прибыл в Выехал из	Париж	Берлин	Рим	Лондон
Париж	∞
Берлин		∞
Рим			∞
Лондон				∞

Вид электронной таблицы, созданной для решения задачи, представлен на рис. 1.

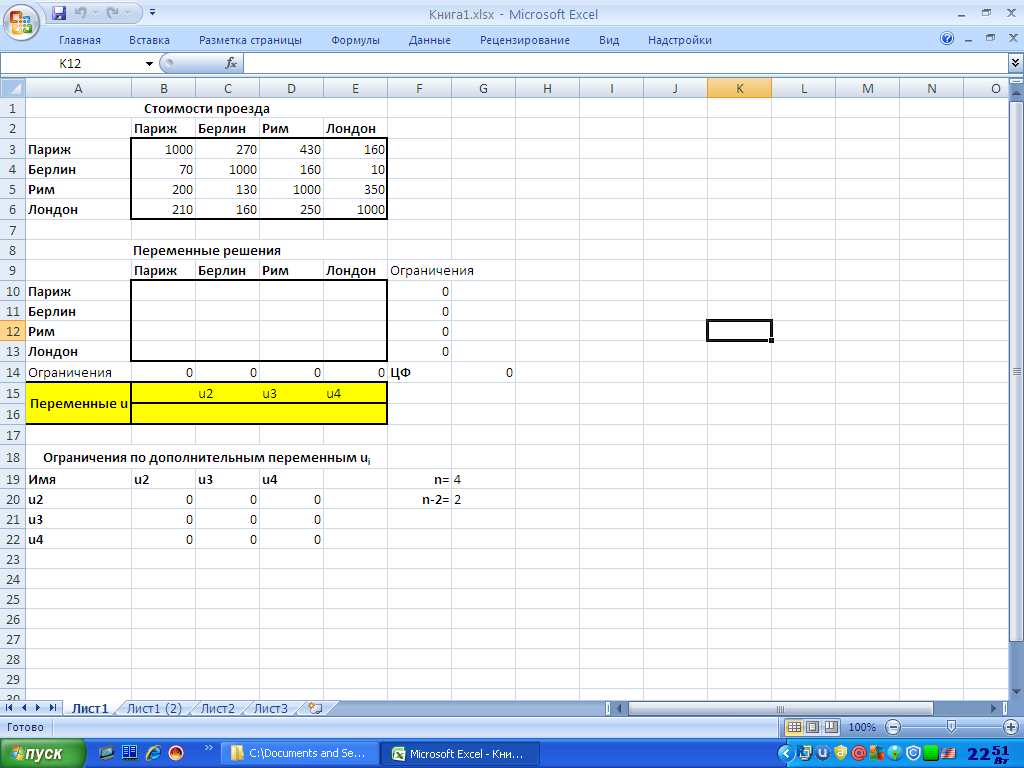
Рисунок 1

Здесь заданы стоимости проезда из города в город (блок B3:E6). Значения переменных 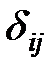располагаются в блоке B10:E13.

Для вычислений необходимо задать размерность задачи n (количество городов) — ячейка G19.

Целевая функция расположена в ячейке G14. Ограничения находятся в блоках B14:E14 (коммивояжер въезжает один раз в каждый город) и F10:F13 (коммивояжер выезжает из каждого города один раз). В задаче коммивояжера есть ряд специфических ограничений по дополнительным переменным 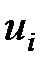(см. мат модель). Формулы этих ограничений находятся в блоке ячеек B20:D22. Значения самих переменных располагаются в блоке C16:E16.

Вид электронной таблицы в режиме отображения формул представлен на рис. 2.

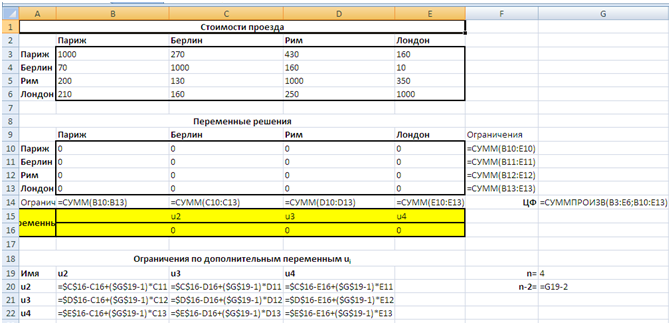
Рисунок 2

На рис. 3 представлена запись условий задачи в окне «Поиск решения». Хотя дополнительные переменные не относятся к целевой функции, они, также как и 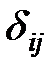, являются изменяемыми, поэтому адреса содержащих их ячеек должны быть введены в поле Изменяя ячейки одновременно с адресами переменных целевой функции (через «;»).

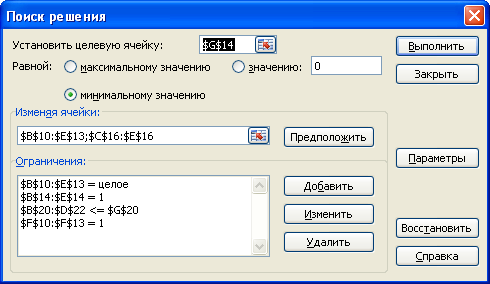
Рисунок 3

По результатам поиска решения найден ответ задачи: из Парижа коммивояжер летит в Лондон, оттуда в Рим, затем в Берлин, откуда возвращается в Париж. Общая стоимость перелета составит 610 д. е. (см. рис. 4).

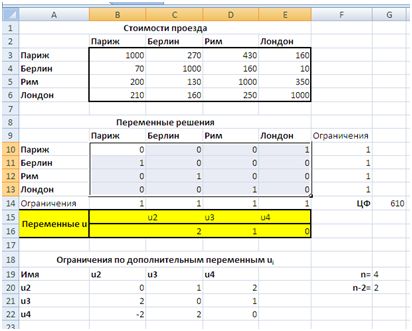
Рисунок 4

П

Л

Р

Б