Показательный (экспоненциальный) закон распределения
Непрерывная случайная величина X имеет показательный (экспоненциальный) закон распределения, если ее плотность вероятности 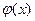 имеет вид:
имеет вид:
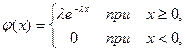
где 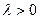 - параметр данного распределения.
- параметр данного распределения.
Функция распределения F(x) случайной величины X, распределенной по показательному закону, находится по формуле
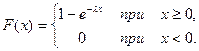 (14)
(14)
Важнейшие числовые характеристики показательного распределения определяются равенствами:
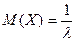 ,
, 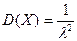 ,
, 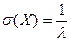 . (15)
. (15)
Для показательного закона распределения вероятность того, что случайная величина X примет значение, принадлежащее интервалу (a, b), определяется формулой
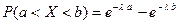 .
.
Нормальный закон распределения
Нормальный закон распределения (закон Гаусса) играет исключительную роль в теории вероятностей. Главная особенность закона Гаусса состоит в том, что он является предельным законом, к которому приближаются, при определенных условиях, другие законы распределения. Нормальный закон распределения наиболее часто встречается на практике.
Непрерывная случайная величина X имеет нормальный закон распределения (закон Гаусса) с параметрами 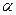 и
и 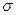 , если ее плотность вероятности имеет вид:
, если ее плотность вероятности имеет вид:
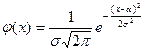 .
.
Кривую нормального закона распределения называют нормальной кривой или кривой Гаусса.
Нормальная кривая 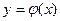 изображена на рис. 9.
изображена на рис. 9.
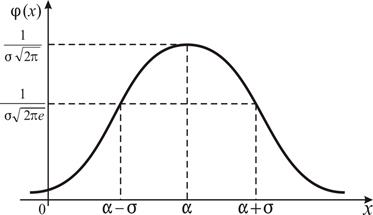
Рис. 9
Тот факт, что случайная величина X распределена по нормальному закону с параметрами 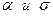 , коротко записывают так:
, коротко записывают так: 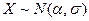 .
.
Математическое ожидание случайной величины X, распределенной по нормальному закону, равно параметру 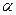 этого закона, т. е.
этого закона, т. е. 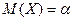 , а дисперсия – параметру
, а дисперсия – параметру 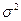 , т. е.
, т. е. 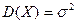 .
.
Нормальный закон распределения случайной величины с параметрами 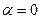 и
и 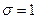 , т. е. случайной величины
, т. е. случайной величины 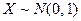 называется стандартным или нормированным.
называется стандартным или нормированным.
Плотность стандартной случайной величины X имеет вид
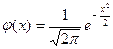
и называется функцией Гаусса.
Вероятность попадания в интервал (a, b) случайной величины X, подчиненной нормальному закону, определяется формулой
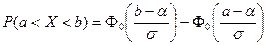 , (16)
, (16)
где функция 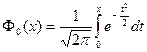 называется функцией Лапласа(или интегралом вероятности). Эту функцию называют также функцией ошибок.
называется функцией Лапласа(или интегралом вероятности). Эту функцию называют также функцией ошибок.
Функция Лапласа обладает следующими свойствами:
1. 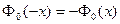 , т. е. функция
, т. е. функция 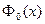 - нечетная;
- нечетная;
2. 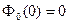 ; 3.
; 3. 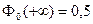 .
.
Таблицу значений функции Лапласа можно найти в приложении 1.
Вероятность попадания случайной величины 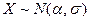 в интервал
в интервал 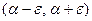 , симметричный относительно центра рассеяния
, симметричный относительно центра рассеяния 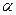 , находится по формуле
, находится по формуле
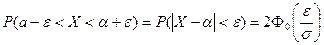 . (17)
. (17)
В частности, 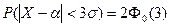
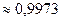 , т. е. практически достоверно, что случайная величина
, т. е. практически достоверно, что случайная величина 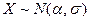 принимает свои значения в интервале
принимает свои значения в интервале 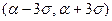 . Это утверждение называется “правилом трех сигм”.
. Это утверждение называется “правилом трех сигм”.
Решение задач
Пример 1. 30% изделий, выпускаемых данным предприятием, нуждается в дополнительной регулировке. Наудачу отобрано 200 изделий. Найти среднее значение и дисперсию случайной величины X – числа изделий в выборке, нуждающихся в регулировке.
Решение.Случайная величина X имеет биномиальное распределение. Здесь n=200, p=0,3, q=0,7. Используя формулы (10), находим: 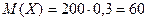 ,
, 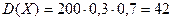 .
.
Пример 2. Автоматическая телефонная станция получает в среднем за час 300 вызовов. Какова вероятность того, что за данную минуту она получит точно два вызова?
Решение.За одну минуту АТС в среднем получает 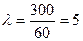 вызовов. Считая, что случайное число X вызовов, поступивших на АТС за одну минуту, подчиняется закону Пуассона, по формуле (11) найдем искомую вероятность
вызовов. Считая, что случайное число X вызовов, поступивших на АТС за одну минуту, подчиняется закону Пуассона, по формуле (11) найдем искомую вероятность 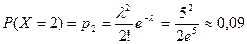 .
.
Пример 3. Вероятность попадания в цель при одном выстреле равна 0,01. Какова вероятность того, что число попаданий при 200 выстрелах составит не менее 5 и не более 10?
Решение.Пусть случайная величина X – число попаданий в цель. Так как вероятность p=0,01 очень мала, а число выстрелов (опытов) достаточно велико, то искомую вероятность будем находить, используя формулу Пуассона (см. (11)). По теореме сложения вероятностей 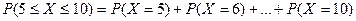 . Учитывая, что
. Учитывая, что 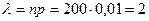 ,
, 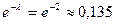 , получим
, получим 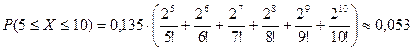 .
.
Пример 4. Поезда метрополитена идут регулярно с интервалом 2 мин. Пассажир выходит на платформу в случайный момент времени. Какова вероятность того, что ждать пассажиру придется не больше полминуты? Найти математическое ожидание и среднее квадратическое отклонение случайной величины X – времени ожидания поезда.
Решение.Случайная величина X – время ожидания поезда – на временном отрезке [0, 2] имеет равномерный закон распределения 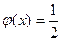 (см. (12)). Тогда вероятность того, что пассажиру придется ждать не более полминуты
(см. (12)). Тогда вероятность того, что пассажиру придется ждать не более полминуты
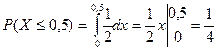 .
.
По формулам (13) найдем 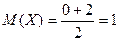 мин.,
мин., 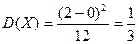 .
.
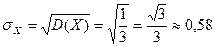 мин.
мин.
Пример 5. Случайная величина T – время работы радиолампы – имеет показательное распределение. Определить вероятность того, что время работы лампы будет не меньше 600 часов, если среднее время работы радиолампы 400 часов.
Решение.По условию задачи математическое ожидание случайной величины T равно 400 часам, следовательно, 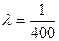 . (см. (15)).
. (см. (15)).
Тогда с учетом формулы (14) искомая вероятность 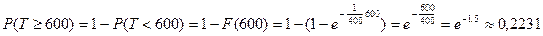 .
.
Пример 6. Случайные ошибки измерения детали подчинены нормальному закону с параметром 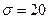 мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
мм. Найти вероятность того, что измерение детали произведено с ошибкой, не превосходящей по модулю 25 мм.
Решение.Воспользуемся формулой (17). В нашем случае 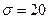 ,
, 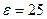 , следовательно,
, следовательно,
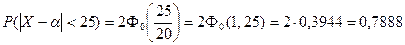 .
.
Пример 7. Пусть X – случайная величина, подчиненная нормальному закону с математическим ожиданием 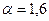 и средним квадратическим отклонением
и средним квадратическим отклонением 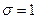 . Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
. Какова вероятность того, что при четырех испытаниях эта случайная величина попадет хотя бы один раз в интервал (1,2)?
Решение.Найдем вероятность попадания случайной величины X в интервал (1,2) при одном испытании. Согласно формуле (16) имеем:
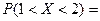
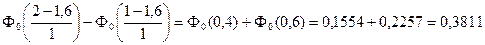 .
.
Тогда вероятность того, что случайная величина не попадет в интервал (1,2) при одном испытании равна 1-0,3811=0,6189, а при четырех испытаниях 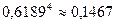 . Значит, искомая вероятность
. Значит, искомая вероятность 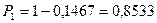 .
.
