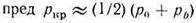Критическая нагрузка и её связь с физико-механическими свойствами грунта

Предельная критическая на­грузка ри соответствует напряжению под подошвой фундамента, при котором происходит исчерпание несущей способности грунтов основания.

При этом в основании формируются развитые области предельного равновесия, что сопровождается при относительно небольшой глубине заложения фундамента выдав­ливанием грунта на поверхность основания и образованием валов выпирания.

Таким образом, нагрузка, соответст­вующая, приводит к полной по­тере устойчивости грунта основа­ния и является абсолютно недопу­стимой для проектируемого сооружения.

Экспериментальные исследования показали, что пренебрежение собственным весом грунта основания приводит к занижению пре­дельной критической нагрузки. Кроме того, оказалось необходи­мым учитывать наличие под подошвой фундамента формирующе­гося в пределах области ОАВ уплотненного ядра грунта.

Наиболее полное решение получено в 1952 г. В. В. Соколовским для случая плоской задачи при действии на поверхности наклонен­ной под углом к вертикали нагрузки, изменяющейся по закону трапеции. В этом случае вертикальная составляющая предельной критической нагрузки в любой точке загруженной поверхности с координатой x и соответствующая ей горизон­тальная составляющая могут быть приведены к виду.

Отметим, что при этом имеет место формирование области предельного равновесия и возможно выпирание грунта лишь в одну сторону, противоположную направлению возрастания нагрузки.

Известны и другие решения указанной задачи, однако запись выражения для вертикальной критической нагрузки в форме перво­го уравнения сейчас является общепринятой. В практических расчетах величину ри часто заменяют вертикальной силой пред­ставляющей собой равнодействующую предельной критической на­грузки, действующей по некоторой площади загружения.

Приведенные выше решения справедливы при относительно не­больших глубинах заложения фундаментов и однородном строении основания, поэтому в практических расчетах обычно используют инженерные способы, в той или иной мере учитывающие строгие решения теории предельного равновесия.

Ранее, были рассмотрены механические явления, возникающие в грунтах при возрастании на них местной нагрузки, причем установлены две критические нагрузки: 1 — нагрузка, соответ­ствующая началу возникновения в грунте зон сдвигов и окончанию фазы уплотнения, и 2 — нагрузка, при которой под нагруженной поверхностью сформировываются сплошные области предельного равновесия, грунт приходит в неустойчивое состояние и полностью исчерпывается его несущая способность.

Величину первой нагрузки назовем начальной критической нагрузкой, а вторую, при которой исчерпывается полностью несущая способность грунта, — предельной критической нагрузкой на грунт.

Как уже отмечалось выше (подразд. 2.2.2), по мере загружения фундамента наблюдаются две критические нагрузки: нагрузка, соответствующая началу возникновения в грунте зон сдвига и окончания фазы уплотнения, и нагрузка, при которой под нагруженным фундаментом сформировываются сплошные области предельного равновесия, происходит потеря устойчивости грунтов основания и исчерпывается его несущая способность.

Начальная критическая нагрузка соответствует случаю, когда в основании под подошвой фундамента возникает предельное состояние. Эта нагрузка еще безопасна в основаниях сооружения, так как до ее достижения грунт всегда находится в фазе уплотнения. При нагрузках, меньших начальной критической, во всех точках основания напряженные состояния допредельные и деформируемость грунта подчиняется закону Гука. Следовательно, для определения начальной критической нагрузки могут быть использованы решения задач теории упругости.

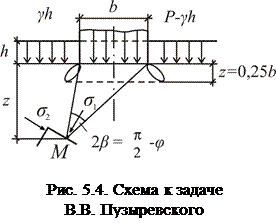Определение р_кр дано в решении В.В.Пузыревского (рис. 5.4). Грунт рассматривается как однородное, изотропное тело. Нагрузка принята полосовой с интенсивностью р. Поскольку фундамент заглублен на глубину d, то давление будет р – γd. Для произвольной точки М, расположенной на глубине z и характеризуемой углом видимости 2β, главные напряжения с учетом напряжений от собственного веса грунта будут равны

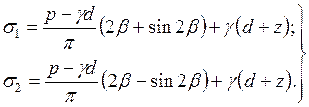(5.5)

Подставив 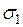и 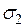в уравнение предельного равновесия (5.4), учтем, что давление связности 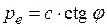, решив его относительно р = р_кр , при z = 0 получим формулу В.В. Пузыревского

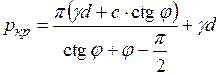, (5.6)

где 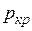– начальная критическая нагрузка; 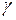– удельный вес грунта; d – глубина заложения фундамента; 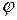– угол внутреннего трения грунта; с – сцепление грунта.

Следует иметь в виду, что начальная критическая нагрузка соответствует пределу пропорциональности между напряжениями и деформациями грунта, а давление, равное начальному критическому давлению или меньше его, рассматривается как безопасное.

Строительные нормы СНиП 2.02.01 - 83^* допускают развитие пластических деформаций в краевых участках фундаментов на глубину 0,25 ширины фундамента b. Такая нагрузка соответствует расчетному сопротивлению грунта R. Его уравнение с учетом развития областей предельного равновесия на глубину z = 0,25bимеет вид

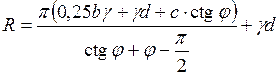. (5.7)

Для практического использования в расчетах формулу (5.7) представляют в виде

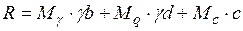, (5.8)

где 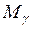, , 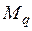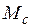– коэффициенты несущей способности, зависящие от угла внутреннего трения 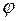и вычисляемые по формулам

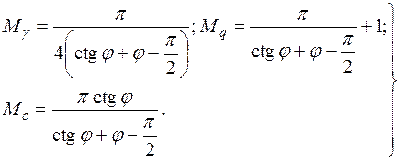(5.9)

Численные значения коэффициентов 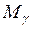, 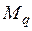и 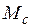приведены в табл. 4 СНиП 2.02.01 - 83^*.

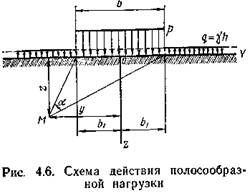
Начальная критическая нагрузка на грунт. Рассмотрим действие равномерно распре­деленной нагрузки р на полосе шириной b (рис. 4.6) при наличии боковой пригрузки q=γh (где γ — плотность грунта; h — глубина залегания нагруженной поверхности).

Вертикальное сжимающее напряжение (давление) от собственного веса грунта при горизонтальной ограничивающей поверхности

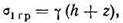
где z — глубина расположения рассматриваемой точки ниже плоскости приложения нагрузки.

Задача будет заключаться в определении такой нагрузки, при которой зоны сдвига (зоны предельного равновесия) только зарождаются под нагруженной поверхностью.

Примем дополнительное допущение о гидростатическом распре­делении давлений от собственного веса грунта, а именно

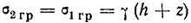
При сделанном допущении задача впервые решена проф. Н. П. Пузыревским (1929), затем Н. М. Герсевановым (1930) и позднее О. К. Фрелихом (1934).

Примем условие предельного равновесия:

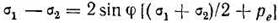
Для произвольной точки М (рис. 4.6), найдем главные напряжения с учетом действий собственного веса грунта как сплошной нагрузки:

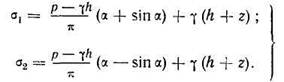
Подставим значения σ₁ и σ₂ в условие предельного равновесия, и принимая во внимание, чтоp_e=c·ctgφ, получим

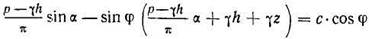
Решая уравнение относительно z, получим

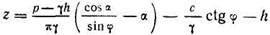
Выполнив соответствующие математические преобразования и решая уравнение относительно величины р=р_кр, получим

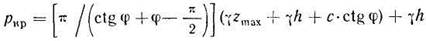
Проф. Н. Н. Маслов допускает z_max=btgφ.

Называя наибольшее давление, при котором ни в одной точке грунта не будет зон предельного равновесия (z_max=0), начальным критическим давлением на грунт начp_кр, получим

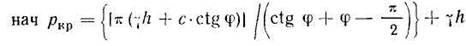
Это и есть формула проф. Н. П. Пузыревского для начальной критической нагрузки на грунт. Определяемое по ней давление можно рассматривать как совершенно безопасное в основаниях сооружений; никаких добавочных коэффициентов запаса в этом случае вводить не следует.

Для идеально связных грунтов (для которых φ≈0) условие предельного равновесия будет:

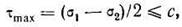
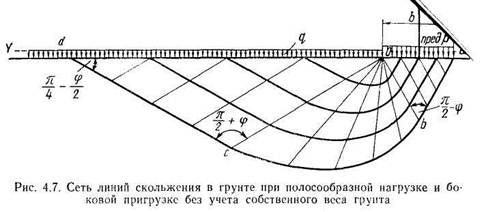
Тогда

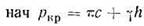
Данную формулу часто используют при определении расчетного (безопасного) давления для глинистых грунтов с малым углом внутреннего трения (до 7°), а также для грунтов вечномерзлых (при сохранении их отрицательной темпе­ратуры) с учетом релаксации сил сцепления, подставляяс_дл вместо с.

Предельная нагрузка для сыпучих и связных грунтов. Второй критической нагрузкой на грунт, как было рассмотрено ранее, следует считать предельную нагрузку, соответствующую полному исчерпанию несущей способности грунта

Решение дифференциальных уравнений равновесия совместно с условиями предельного равновесия позволяет найти математически точные очертания поверхностей скольжения, используя которые, можно достаточно строго оценить значение предельной нагрузки (давления) на грунт, соответствующее максимальной несущей способности основания.

Впервые эта задача для невесомого грунта, нагруженного полосообразной нагрузкой (предельная величина которой определяется), была решена Прандтлем и Рейснером (1920—1921), причем для предельной нагрузки на грунт получено следующее выражение:

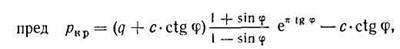
где q — боковая пригрузка, равная γh (h — глубина приложения полосообразной нагрузки, рис. 4.7).

В частном случае для идеально связных грунтов (φ=0 и c≠0) предельная нагрузка для условий плоской задачи (при полосообразном загружении), по Прандтлю, будет равна:

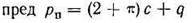
Для осесимметричной пространственной задачи (круг, квадрат) предельная нагрузка в случае идеально связных грунтов (по А. Ю. Ишлинскому, 1947)

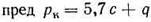
В случае водонасыщенных глинистых грунтов и нестабилизированного их состояния (когда внутреннее трение не реализуется) предельная нагрузка на грунт под круглыми и равновеликими им квадратными фундаментами, по А. С. Строганову

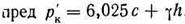
При действии наклонной нагрузки с боковой пригрузкой на грунт, обладающий трением и сцеплением (рис. 4.8), решение получено В. В. Соколовским (1952) как сумма предельной нагрузки для идеально сыпучего грунта с учетом действия его собственного веса и предельной нагрузки для связного грунта, но без учета его веса.

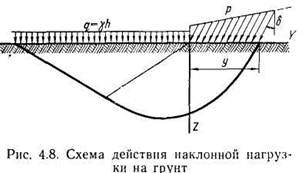
Вертикальная составляющая предельной нагрузки при этом определяется следующим выражением:

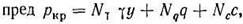
где N_γ, N_q, N_c — коэффициенты несущей способности грунта, определяемые путем вычисления по построенной сетке линий скольжения как функции угла внутреннего трения и наклона нагрузки.

Форма данного уравнения, впервые предложенная проф. Терцаги (1943), в настоящее время является канонической и к ней обычно приводятся все другие решения, полученные для предельной нагрузки на грунт при иных граничных условиях и ином загружении.

Горизонтальная составляющая предельного давления на грунт в случае действия полосообразной наклонной нагрузки определится по формуле

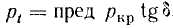
где δ — угол наклона полосообразной нагрузки к вертикали (рис. 4.8).

Получаемые по приведённой формуле значения предp_кр соответствуют достаточно строгому решению для наклонной полубесконечной нагрузки (рис. 4.8), что на практике соответствует лишь случаю очень широкой площади подошвы сооружения.

Для края наклонной нагрузки (полагая y=0) имеем:

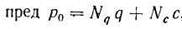
а для ординаты, соответствующей ширине фундамента (т. е. при y=b), при условии отсутствия выпирания в противоположную сторону

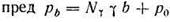
Тогда средняя величина вертикальной составляющей предельного давления на грунт