Примеры построения экономико-математических моделей

Задача №1.1.

Задача о наилучшем использовании ресурсов

Для изготовления двух видов продукции 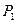и и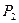спользуют четыре вида ресурсов 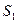, , 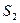, , 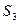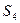которые имеются в количестве 22, 26, 16, 12 усл. ед. соответственно. На изготовление одной единицы продукции 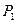требуется 1 ед. ресурса 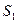, 2 ед. ресурса 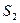и 1 ед. ресурса 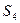. Для изготовления одной единицы 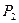необходимо 2 единицы ресурса 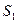, 1 ед. ресурса 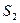и 2 ед. ресурса 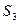. Прибыль, получаемая при реализации одной единицы продукции 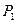и продукции 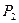, составляет 4 д.е. и 3 д.е., соответственно. Необходимо составить такой план производства продукции, при котором прибыль при ее реализации была бы максимальной. Построить экономико-математическую модель задачи.

Решение.

Запишем условие задачи в виде таблицы:

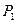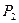			запасы
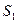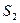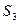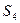прибыль

Построим экономико-математическую модель задачи.

Введем переменные 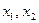усл. ед. - запланированные объемы производства продукци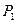и и 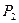соответственно.

В принятых обозначениях:

1) 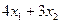д.е. - прибыль, получаемая при реализации всей продукци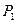и и ;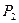

2) 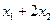ед. – затраты ресурса 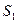на изготовление всей запланированной к производству продукции;

3) 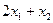ед.- затраты ресурса 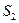на изготовление всей запланированной к производству продукции;

4) 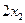ед. - затраты ресурса 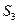на изготовление всей запланированной к производству продукции;

5) 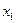ед. - затраты ресурса 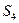на изготовление всей запланированной к производству продукции;

6) переменные 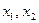- по смыслу задачи, неотрицательны.

Учитывая то, что прибыль необходимо максимизировать, а так же ограничения на ресурсы, строим математическую модель задачи:

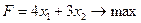(1.3)

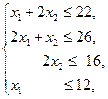(1.4)

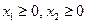. (1.5)

Экономико-математическая модель задачи: найти план выпуска продукции 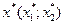, удовлетворяющий условиям (1.3) – (1.5).

Задача №1.2.

Задача о составлении рациона питания

При откорме каждое животное в дневном рационе должно получить не менее 9 ед. белков, 8 ед. углеводов и 11 ед. протеина. Для составления ра­циона используют два вида корма, представленных в следующей таблице:

Питательные вещества	Количество единиц питательных веществ на 1 кг
корма	корма
Белки Углеводы Протеин

Стоимость 1 кг корма первого вида составляет 4 д.е., второго - 6 д.е. Составить дневной рацион питания, имеющий минимальную стоимость. Построить экономико-математическую модель задачи.

Решение.

Введем переменные 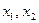кг – количество корма вида и количество корма вида соответственно, входящие в состав дневного рациона.

В принятых обозначениях дневной рацион корма должен содержать:

1) 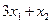единиц белка;

2) 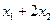единиц углеводов;

3) 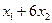единиц протеина.

Стоимость дневного рациона составляет 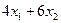д.е.

Переменные 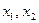- по смыслу задачи, неотрицательны.

Минимизируя стоимость дневного рациона, а также, учитывая, что при откорме каждое животное должно получить не менее 9 ед. белков, 8 ед. углеводов и 11 ед. протеина, строим математическую модель задачи:

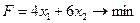(1.6)

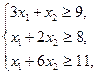(1.7)

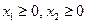. (1.8)

Экономико-математическая модель задачи: составить дневной рацион откорма животных 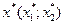, удовлетворяющий условиям (1.6) – (1.8).

Задача №1.3.

Задача о смесях

Предприниматель собирается производить сплав, содержащий 30% свинца. 30% цинка и 40% олова.

На рынке имеются сплавы 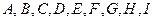. Процентное содержание свинца, цинка, олова, а также стоимость одного кг сплава указаны в таблице

сплав	A	B	C	D	E	F	G	H	I	Необходимо
№
% свинца
% цинка
% олова
cтоим. за 1 кг в д.е.	4.1	4.3	5.8	6.0	7.6	7.5	7.3	6.9	7.3

Какое количество сплава каждого типа стоит закупить на каждый кг, производимого комбинированного сплава для минимизации затрат. Построить экономико-математическую модель задачи.

Решение

Введем обозначения: 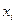кг - объем закупки 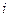-го из имеющихся на рынке сплавов 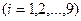, на один кг производимого комбинированного сплава. Отсюда сразу же получаем ограничение на объем закупки каждого из имеющихся на рынке сплавов на один кг производимого комбинированного сплава: .

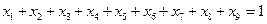Равенства ;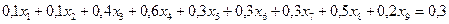

;

,

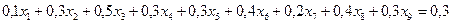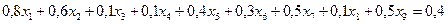отражают соответственно тот факт, что в одном кг производимого комбинированного сплава доля свинца составляет ровно 30%; цинка 30%; олова 40% соответственно.

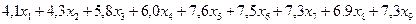д.е. – затраты на один кг, производимого комбинированного сплава.

Экономико-математическая модель задачи:

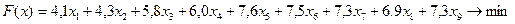(1.9)

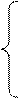
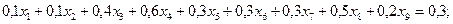
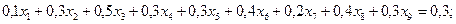(1.10)

.

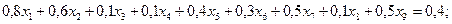
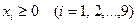Найти объемы закупок 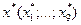каждого вида из имеющихся сплавов на один кг производимого комбинированного сплава, удовлетворяющие условиям (1.9) и (1.10).

Задача № 1.4.

Задача о раскрое материалов

Для изготовления брусьев длиной 1.2 м , 3 м и 5 м в соотношении 2 : 1: 3 на распил поступают 195 бревен длиной 6 м. Определить план распила, обеспечивающий максимальное число комплектов. Построить экономико-математическую модель задачи.

Решение.

Определим всевозможные способы распила бревен, указав соответствующее число получаемых при этом брусьев.

Способ распила i	Число, получаемых брусьев
1.2	3.0	5.0
		-	-
			-
	-		-
	-	-

Обозначим через 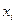- число бревен, распиленных 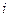-ым способом 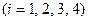; 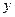– число комплектов брусьев.

Учитывая, что все бревна должны быть распилены, а число брусьев каждого размера должно удовлетворять условию комплектности, экономико-математическая модель задачи примет вид:

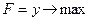(1.11)

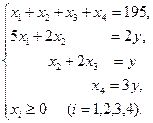(1.12)

Определить оптимальный план распила бревен 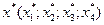, максимизирующий общее число комплектов 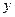и удовлетворяющий ограничениям (1.12).

Задача № 1.5.

На участок строящейся дороги необходимо вывезти 20 000 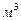каменных материалов. В районе строительства имеются три карьера с запасами 8 000 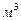, 9 000 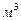и 10 000 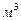. Для погрузки материалов используются экскаваторы, имеющие производительность 250 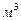в смену в карьерах 1 и 2 и 500 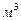в смену в карьере 3.

На погрузку материалов для рассматриваемого участка выделен для экскаваторов общий лимит 60 машинных смен с правом использования его по усмотрению строителей

Транспортные затраты на перевозку материалов характеризуются показателями: для перевозки 10 000 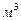материалов из карьера 1 требуется 1000 автомобильных смен, из карьера 2 – 1350, из карьера 3 – 1700. Требуется найти оптимальный план перевозок, обеспечивающий минимальные транспортные затраты. Построить экономико-математическую модель задачи.

Решение.

Примем за единицу измерения количества материалов равное 10 000 .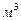

Обозначим 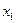, , 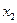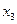ед. - объемы добычи материалов в карьере 1, 2, 3 соответственно.

Равенство 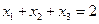в принятых обозначениях означает, что на участок строящейся дороги необходимо вывезти 2 ед. каменных материалов.

По условию задачи для погрузки материалов используются экскаваторы, имеющие производительность 0,025 ед. в смену в карьерах 1 и 2 и 0,05 ед. в смену в карьере 3.

Ограничение по наличию ресурса «фонд рабочего времени экскаваторов» не должен превышать 60 машинных смен, можно записать в виде .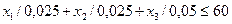

По условию задачи, запас материалов в карьерах ограничен. Этот факт в принятых обозначениях отражают ограничения:

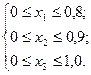
Полные транспортные затраты в количестве автомобильных смен составят:

.

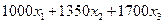Экономико-математическая модель задачи:

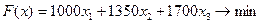(1.11)

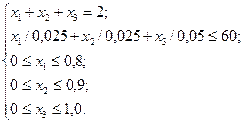(1,12)

Найти оптимальные объемы добычи материалов 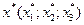, удовлетворяющие условиям (1.11) и (1.12).

Задача №1.6.

Рассматривается проблема принятия инвестором решения о вложении, имеющегося у него капитала. Набор характеристик потенциальных объектов для инвестирования, имеющих условные наименования от 1 до 6 , задается следующей таблицей.

№	Доходность за один год в %	срок выкупа	надежность в баллах

При принятии решения о приобретении активов должны быть соблюдены условия:

а) суммарный объем капитала, который должен быть вложен, составляет 100 000 д.е.;

б) доля средств, вложенных в один объект, не может превышать четверти от всего объема;

в) более половины всех средств должны быть вложены в долгосрочные активы (допустим, на рассматриваемый момент к таковым относятся активы со сроком погашения после 2010);

г) доля активов имеющих надежность менее чем 3 балла, не может превышать трети от суммарного объема.

Необходимо максимизировать суммарный доход инвестора от размещения активов. Построить экономико-математическую модель задачи.

Решение.

Введем обозначения: 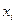д.е. - объемы средств, вложенные в активы 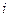-ой фирмы.

В принятых обозначениях:

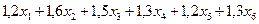д.е. – суммарный доход.

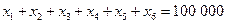д.е. - суммарный объем капитала, вложенный в перечисленные активы.

Условия того, что доля средств, вложенных в один объект, не может превышать четверти от всего объема, можно представить в виде системы неравенств:

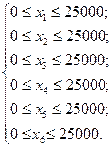
Условие того, что более половины всех средств должны быть вложены в долгосрочные активы, можно записать в виде неравенства: .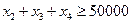

Так как доля активов имеющих надежность менее чем 3 балла, не может превышать трети от суммарного объема, то должно выполняться неравенство:

.

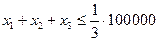Экономико-математическая модель задачи:

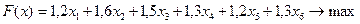(1.13)

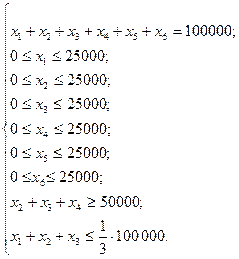(1.14)

Найти объемы средств 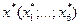, вложенные в активы, удовлетворяющие условиям (1.13) и (1.14).

Задача № 1.7.

Из пункта А в пункт В ежедневно отправляются пассажирские и скорые поезда. Данные об организации перевозок следующие:

Поезда	Количество вагонов в поезде
багажный	почтовый	плацкар	купейн.	мягкий
Скорый
Пассажирский		-
Число пассажиров	-	-
Парк вагонов

Сколько должно быть сформировано скорых и пассажирских поездов, чтобы перевезти наибольшее количество пассажиров? Построить экономико-математическую модель задачи.

Решение.

Пусть 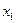- количество сформированных скорых поездов; 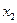- пассажирских поездов.

Математическая модель задачи:

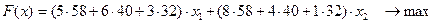
при условии выполнения ограничений:

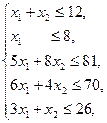
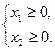
Задача № 1.8.

Транспортная задача

Четыре овощехранилища каждый день обеспечивают картофелем три магазина. Магазины подали заявки на доставку картофеля на 17, 12, 32 т., соответственно. Овощехранилища имеют 20, 20, 15 и 25 т. соответственно. Тарифы в д.е. за 1 т. доставки картофеля указаны в таблице:

Овоще - хранилища	магазины

Составить план перевозок, минимизирующий суммарные транспортные расходы. Построить экономико-математическую модель задачи.

Решение.

Пусть 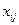т. картофеля доставлено из 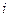-го овощехранилища в 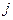-ый магазин .

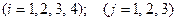Математическая модель задачи:

найти план перевозок 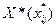, удовлетворяющий условиям

,

.
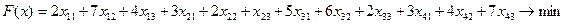
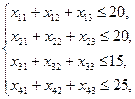
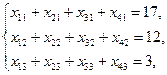
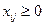
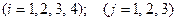