Стандартные функции Matlab

Все операции в Matlab ориентированы прежде всего на работу с матрицами, но могут выть использованы при работе с векторами и скалярными переменными.

Элементарные функции Matlab. К ним относятся следующие функции:

Тригонометрические:

sin(x) sinh(x) asin(x) asinh(x)

cos(x) cosh(x) acos(x) acosh(x)

tan(x) tanh(x) atan(x) atan2(x,y) atanh(x)

cot(x) coth(x) acot(x) acoth(x)

Экспоненциальные:

exp(x) log(x) log10(x) log2(x) pow2(x) sqrt(x)

Функции комплексного аргумента:

abs(z) – модуль комплексного числа; angle(z) – аргумент;

complex(x, y) – формирование комплексного числа x+y*i;

conj(z) – возвращает комплексно-сопряженное (по отношению к z) число;

real(z) – возвращает действительную часть; imag(z) – мнимую часть.

Функции округления и нецелочисленного деления:

fix(x) – округление в сторону к нулю, floor(x) – к –¥, ceil(x) – к +¥,

round(x) – до ближайшего целого;

mod(x, y) – остаток от деления x/y с учетом знака,

rem(x, y) – то же, без учета знака;

sign(x) – знак числа (+1/–1).

Элементарные функции, как и всякие другие, имеют один результат (массив). Элементарные функции могут быть использованы с одинаковым синтаксисом как для чисел, так и для массивов.

Пример 1. Разный тип параметров

» x=-8; X=[5 -1 -2]; A=[1 2 -3; -5 6 7]; z=3-4i;

» abs(x)

ans =

» abs(X)

ans =

5 1 2

» abs(A)

ans =

1 2 3

5 6 7

» abs(z)

ans =

Арифметические операции

Различают матричные и поэлементные арифметические операции.

+ – уточнение знака (унарная), сложение;

– – изменение знака (унарная), вычитание;

Поскольку математический смысл операций матричного и поэлементного сложения и вычитания идентичен:

C = A ± B означает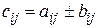

синтаксис матричных и поэлементных операций сложения и вычитания одинаков, в них используются одни и те же символы операций.

* – скалярное матричное умножение;

.* – поэлементное умножение;

^ – матричное возведение в степень;

.^ – поэлементное возведение в степень;

\ – матричное деление слева;

/ – матричное деление справа;

./ – поэлементное деление;

' – транспонирование (унарная);

.' – несопряженное транспонирование (унарная).

Все арифметические операции, за исключением указанных, являются бинарными.

В операциях +, –, .*, ./ и .^ либо оба операнда должны иметь одинаковую размерность, либо один из операндов должен быть скалярной величиной.

Например,

» A=[1 2 3; 4 5 6]; B=[7 8 9; 3 2 1];

» A+B

ans =

8 10 12

7 7 7

» B-A

ans =

6 6 6

-1 -3 -5

» A+2

ans =

3 4 5

6 7 8

» A.*B

ans =

7 16 27

12 10 6

» A.*2

ans =

2 4 6

8 10 12

» B./A

ans =

7.0000 4.0000 3.0000

0.7500 0.4000 0.1667

» B./10

ans =

0.7000 0.8000 0.9000

0.3000 0.2000 0.1000

» B.^A

ans =

7 64 729

81 32 1

» A.^2

ans =

1 4 9

16 25 36

Для операции * (матричное произведение) матрица-сомножитель2 должна иметь столько строк, сколько столбцов имеет матрица-сомножитель1:

Z_m*n = X_m*k*Y_k*n

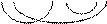Поэтому

» A*B

??? Error using ==> *

Inner matrix dimensions must agree.

» A*B'

ans =

50 10

122 28

» A'*B

ans =

19 16 13

29 26 23

39 36 33

Операции транспонирования ' и .' для матриц с действительными коэффициентами абсолютно равнозначны:

» D=[1 2; 3 4; 5 6];

» D'

ans =

1 3 5

2 4 6

» D.'

ans =

1 3 5

2 4 6

Для комплексных чисел и матриц с комплексными коэффициентами операция ' дает транспонированную сопряженную матрицу, а операция .' – транспонированную несопряженную:

» x=2+3i;

» xt=x'

xt =

2.0000 - 3.0000i

» xtt=x.'

xtt =

2.0000 + 3.0000i

» Ac=[1+2i 1+3i 1+4i; 2+3i 2+4i 2+5i];

» Act=Ac'

Act =

1.0000 - 2.0000i 2.0000 - 3.0000i

1.0000 - 3.0000i 2.0000 - 4.0000i

1.0000 - 4.0000i 2.0000 - 5.0000i

» Actt=Ac.'

Actt =

1.0000 + 2.0000i 2.0000 + 3.0000i

1.0000 + 3.0000i 2.0000 + 4.0000i

1.0000 + 4.0000i 2.0000 + 5.0000i

Операция ^ (матричное возведение в степень) выполняется только для квадратных матриц, и означает умножение матрицы саму на себя заданное число раз (второй операнд обязательно скаляр):

» D=[1 2; 3 4];

» D^2

ans =

7 10

15 22

» D^(-8.58)

ans =

1.0e+003 *

-0.9100 - 3.5442i 0.4163 + 1.6212i

0.6244 + 2.4318i -0.2856 - 1.1124i

Операция

» D^(-1)

ans =

-2.0000 1.0000

1.5000 -0.5000

генерирует обратную матрицу D^-1.

Операция X/Y эквивалентна X*Y^-1, операция X\Y – операции X^-1*Y.

Последняя операция широко используется при решении систем линейных уравнений вида

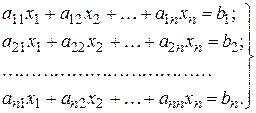
Действительно, представив систему уравнений в матричной форме:

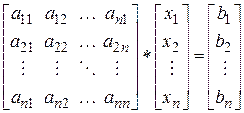
или

A * X = B,

и умножив обе части последнего уравнения на A^-1 слева, получим:

A^-1 * A * X = A^-1 * B,

откуда решение системы уравнений:

X = A^-1 * B.

Пример. Решить систему уравнений

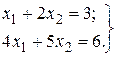
Решение сводится к набору в интерактивном режиме следующих команд:

» A=[1 2; 4 5]; B=[3; 6];

» X=A\B

X =

-1

Проверку вычисления корней можно выполнить следующим образом:

» A*X

ans =

Логические операции

& – логическое "и" (0&0 – 0, 1&0 – 0, 0&1 –1, 1&1 – 1);

| – логическое "или" (0|0 – 0, 1|0 – 1, 0|1 – 1, 1|1 – 1);

xor – логическое исключающее "или" (0xor0 – 0, 0xor1 – 1, 1xor0 – 1, 1xor1 – 0);

~ – логическое отрицание (~0 –1, ~1 – 0).

Если логические операции (а также логические функции) выполняются над действительными числами, то ложью считают число нуль, а истиной – все числа, не равные нулю.

Операции отношения (сравнения)

> – больше; >= – больше или равно; < – меньше; <= – меньше или равно;

= = – равно; ~= – не равно.

Результатом операций отношения является истина (1), если отношение верно, и ложь (0) – в противном случае.

При сравнении двух массивов одинакового размера результатом является массив того же размера, состоящий из нулей и единиц, как результатов поэлементных операций сравнения. Если же в этом случае один из операндов – скаляр, то каждый элемент массива поочередно сравнивается со скаляром.

» 2>1

ans =

» 1>=3

ans =

» A=[1 8 3; 6 2 5]; B=[4 3 1; 2 6 8];

» A>3

ans =

0 1 0

1 0 1

» A<B

ans =

1 0 0

0 1 1

Анализ размерности матриц

length(x) – возвращает длину вектора x;

size(A) – возвращает размеры матрицы A по каждому измерению.

» x=[2 5 8];

» A=[1 2 3; 4 5 6];

» nx=length(x)

nx =

» sx=size(x)

sx =

1 3

» [m,n]=size(A)

m =

n =

» m1=size(A,1)

m1 =

» n1=size(A,2)

n1 =

Дополнительно (не читать):

» m2=length(A)

m2 =

» m2=length(A')

m2 =

» B=[1 2; 3 4; 5 6; 7 8];

» lb=length(B)

lb =

Начиная с версии Matlab 5.0, для обращения к последнему элементу массива используется предопределенная переменная end:

» x(end)

ans =

» A(1,end)

ans =

» A(end,2)

ans =

Формирование специальных векторов и матриц

linspace(x0,xk) linspace(x0,xk,k)

– создают вектор-строку x, содержащий k элементов (по умолчанию k=100), равномерно распределенных на интервале [x0; xk]. Разница между двумя соседними элементами есть величина постоянная: x(i) – x(i-1) = hx = const. При этом шаг hx= .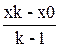

logspace(d0,dk) logspace(d0,dk,k)

– создают вектор-строку xl, содержащий k элементов (по умолчанию k=50), равномерно распределенных вдоль логарифмической оси на интервале [10^d0, 10^dk]. Шаг по показателю степени hd= 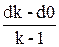. Отношение двух соседних элементов есть величина постоянная 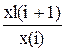=10^hd.

» x=linspace(10,40,4)

x =

10 20 30 40

» xl=logspace(1,4,4)

xl =

10 100 1000 10000

» log10(xl)

ans =

1.0000 2.0000 3.0000 4.0000

zeros – матрица, состоящая из нулей; ones – матрица, состоящая из единиц;

rand – матрица, состоящая из случ. чисел с равномерным распределением;

randn – матрица, состоящая из случ. Чисел с нормальным распределением.

Формат обращения:

zeros(n) – формирует квадратную матрицу n´n, состоящую из нулей;

zeros(m, n) – формирует матрицу m´n, состоящую из нулей;

(zeros(1, n) – вектор-строка; zeros(m, 1) – вектор-столбец)

zeros(size(A)) – формирует матрицу, состоящую из нулей, той же размерности, что и матрица A.

Формат обращения к функциям ones, rand и randn аналогичный.

» Z=zeros(2)

Z =

0 0

0 0

» zeros(1,3)

ans =

0 0 0

» ones(size(Z))

ans =

1 1

1 1

Разницу между функциями rand и randn можно показать графически:

» xr=rand(1,100); xrs=sort(xr); bar(xrs)

» yr=randn(1,100); yrs=sort(yr); bar(yrs)

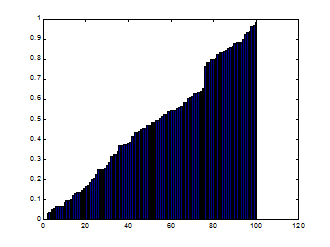
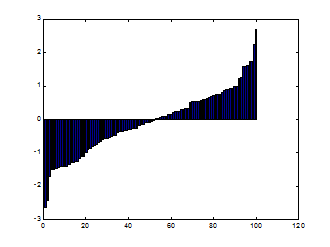
rand randn

eye(n) – формирует единичную диагональную матрицу n´n.

» A=eye(3)

A= 1 0 0

0 1 0

0 0 1

diag(B) (B – двухмерная матрица) – выделяет главную диагональ матрицы B и помещает ее в вектор-столбец;

diag(x) (x – вектор) – формирует диагональную матрицу, используя вектор x в качестве главной диагонали.

» A=[1 2 3; 4 5 6; 7 8 9];

» v=diag(A)

v =

» Av=diag(v)

Av =

1 0 0

0 5 0

0 0 9

Манипуляции с матрицами

tril (A) – формирует треугольную матрицу как нижнюю часть от матрицы A;

triu(A) – формирует треугольную матрицу как верхнюю часть от матрицы А.

» A=[1 2 3; 4 5 6; 7 8 9];

» tril(A)

ans =

1 0 0

4 5 0

7 8 9

» triu(A)

ans =

1 2 3

0 5 6

0 0 9

lu(A) – разложение Холецкого – заменяет квадратную матрицу A скалярным произведением двух треугольных матриц L и U методом Гаусса:

» A=[1 2 3; 4 5 6; 7 8 9];

» [L,U]=lu(A)

L =

0.1429 1.0000 0

0.5714 0.5000 1.0000

1.0000 0 0

U =

7.0000 8.0000 9.0000

0 0.8571 1.7143

0 0 0.0000

» L*U

ans =

1 2 3

4 5 6

7 8 9

inv(A) – возвращает матрицу A^-1, обратную заданной квадратной матрице A;

det(A) – возвращает определитель квадратной матрицы A.

fliplr(A) – поворот матрицы A на 180° в горизонтальном направлении;

flipud(A) – поворот матрицы A на 180° в вертикальном направлении;

rot90(A) – поворот матрицы A на 90° против часовой стрелки;

rot90(A, k) – поворот матрицы A на k*90° против часовой стрелки (k – целое число).

» A=[1 2 3; 4 5 6]

A =

1 2 3 » rot90(A)

4 5 6 ans =

» fliplr(A) 3 6

ans = 2 5

3 2 1 1 4

6 5 4 » rot90(A,3)

» flipud(A) ans =

ans = 4 1

1 2 3 5 2

4 5 6 6 3

Манипуляции с векторами

cross(x, y) – векторное произведение векторов x и y в трехмерном пространстве;

cross(A, B, dim) – векторное произведение многомерных массивов A и B по размерности dim;

dot(x, y) – скалярное произведение векторов x и y;

dot(A, B, dim) – скал. произведение многомерных массивов A и B по размерности dim.

Длины векторов x и y, а также длина матриц A и B по размерности dim должны быть равны 3.

Базовые операции анализа

Пусть a,b,c – числа, х,у,z – векторы, А,В,C – матрицы.

c=max(a, b) – возвращает максимальное из двух чисел a и b (при комплексных аргументах по умолчанию сравниваются модули):

z=max(x, y) – вектор той же размерности, что x и y, составленный из максимальных элементов векторов;

C=max(A, B) – матрица той же размерности, что и , составленная из максимальных элементов матриц.

xmax=max(x) – максимальный элемент вектора x;

[xmax, imax]=max(x) – дополнительно записывает адрес максимального элемента в числовую переменную imax (если максимальных элементов несколько, возвращается адрес первого из них);

amax=max(A) – возвращает вектор-строку amax из максимальных элементов столбцов матрицы А;

[amax, imax]=max(A) – дополнительно формируется вектор-строка imax, составленный из номеров строк, в которых расположены максимальные элементы столбцов.

» a=1; b=2; x=[1 3 2]; y=[2 1 3]; A=[1 2 3; 4 5 6]; B=[3 2 1; 6 5 4];

» c=max(a,b)

c =

» z=max(x,y)

z =

2 3 3

» C=max(A,B)

C =

3 2 3

6 5 6

» xmax=max(x)

xmax =

» [xmax imax]=max(x)

xmax =

imax =

» amax=max(A)

amax =

4 5 6

» [amax imax]=max(A)

amax =

4 5 6

imax =

2 2 2

Работа с функцией min полностью аналогична.

xm=mean(x) – возвращает среднее арифметическое элементов вектора х;

Am=mean(A) – возвращает вектор-строку Am, составленный из средних арифметических элементов столбцов;

» xm=mean(x)

xm =

» Am=mean(A)

Am =

2.5000 3.5000 4.5000

xs=sum(x) – возвращает сумму элементов вектора х;

As=sum(A) – возвращает вектор-строку As, составленный из сумм элементов каждого столбца;

Ads=trace(A) – то же, что sum(diag(A)) – возвращает сумму элементов, расположенных на главной диагонали;

xp=prod(x) – возвращает произведение элементов вектора х;

prod(A) – возвращает вектор-строку Ар, составленный из произведений элементов каждого столбца;

cumsum(x) – кумулятивная сумма (сумма с накоплением) элементов вектора x;

cumprod(х) – кумулятивное произведение (с накоплением) элементов вектора х;

cumsum(A) – кумулятивная сумма элементов матрицы А;

cumprod(A) – кумулятивное произведение элементов матрицы А по столбцам.

» cumsum(x)

ans =

1 4 6

» cumprod(x)

ans =

1 3 6

» cumsum(A)

ans =

1 2 3

5 7 9

» cumprod(A)

ans =

1 2 3

4 10 18

norm(x) – возвращает норму вектора х, равную ;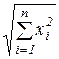

norm(x, p) – возвращает р-норму вектора х, равную ;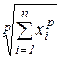

norm(x, Inf) – то же, что max(abs(x)) norm(x,-Inf) – то же, что min(abs(x))

xs=sort(x) – сортировка вектора x по возрастанию;

[xs is]=sort(x) – дополнительно возвращает адреса элементов в исходном массиве х в порядке возрастания элементов;

xsd=fliplr(sort(x)) – сортировка вектора х по убыванию;

y=diff(x) – вычисляет конечные разности:

если 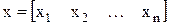, то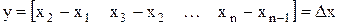

у₁ y₂ у_n-1

z=diff(x,k) – вычисляет k-ю конечную разность:

z=diff(x,2)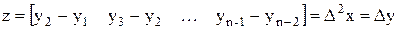

rank(A) – возвращает ранг матрицы – количество линейно независимых строк (столбцов).