Лабораторные работы №1, 2, 3,4

Выполнил: Назарова Т.Ю.

Специальность: 230202.65

Шифр: 0405030025

Оценка:

САНКТ – ПЕТЕРБУРГ

2011г.

Лабораторная работа №1

Интерполяция функций с равноотстоящими узлами методом Ньютона.

1. Цель работы: нахождения аналитического выражения функции, заданной таблицей,используя первую интерполяционную формулу Ньютона.

2. Основные теоретические положения

Постановка задачи:

Пусть функция y=f(x) задана таблично

xi	xo	x1	…	xn
yi	yo= f(xo)	y1= f(x1)	….	yn= f(xn)

Требуется вычислить значения функции для значений аргумента x не совпадающих с заданными в таблице. Для этого неизвестную функцию f(x) заменяют функцией F(x),аналитическое выражение которой известно. Эта функция F(x) называется интерполирующей функцией, а задача ее нахождения - задачей интерполяции. Точки x_{o ,} x_{1,…… ,}x_n при этом называются узлами интерполяции. Интерполяционный многочлен Ньютона ищем в виде:

P_n(x) = a₀ + a₁(x-x₀)+a₂(x-x₀)(x-x₁)+L+a_n(x-x₀)(x-x₁)L(x-x_n-1)

Рассмотрим случай, когда узлы интерполирования равно отстоят друг от друга

x₁ - x₀ - x₂ - x₁ - … - x_n - x_n-1 - h

x₁ = x₀ + ih, h – шаг интерполяции

Конечными разностями первого порядка функции f(x) называются выражения

, = ,

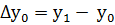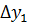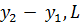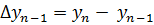
Конечные разности второго порядка

, ,

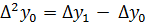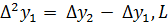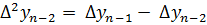
Аналогично, разность порядка m определяется формулой

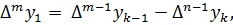k=0,1….n-m.

Тогда коэффициенты 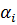можно записать через конечные разности

,

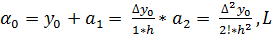
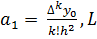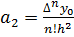
Тогда интерполяционный полином Ньютона имеет вид:

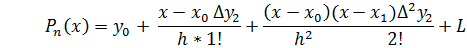
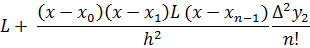
В лабораторной работе необходимо выполнить три задания.

Задание 1. Вычислить конечные разности.

Задание 2. Вычислить коэффициенты интерполяционного многочлена

Задание 3. Вычислить коэффициенты интерполяционного многочлена при заданном значении x.

3.Порядок выполнения работы.

Пример

Используя интерполяционную формулу Ньютона, построить интерполяционный многочлен для функции,заданной таблицей

xi
yi

Вычислить значение интерполяционного многочлена при x =0,3.

Задание 1.Запишем формулу интерполяционного многочлена для четырех узлов интерполяции

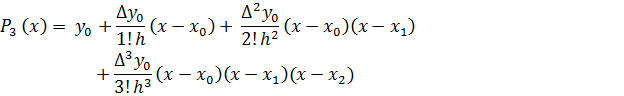
Шаг интерполяции равен h=1. В этом задании нужно вычислить конечные разности первого, второго и третьего порядков

, ,

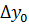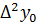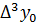
В электронную таблицу внести исходные данные как показано в таблице 1.

Вычислить конечную разность первого порядка 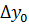в ячейке D9 по формуле =C10-C9

Все остальные конечные разности первого порядка получить копированием D9 в ячейки D10 и D11.

Вычислить конечную разность второго порядка 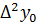копированием D9 в ячейку E9.

Вычислить конечную разность второго порядка 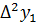копированием E9 в ячейку E10.

Задание 2. Вычислим коэффициенты интерполяционного многочлена по формулам:

, ,

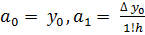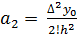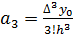
1. В ячейку С16 внесем значение 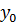из С9.

2. В ячейку D16 внесем формулу для коэффициента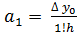

=D9/$B$5^D8/ФАКТР(D8)

Для копирования ячейка B5 должна быть в абсолютных адресах (клавиша F4).

Для вычисления факториала нужно использовать функцию ФАКТР из категории МАТЕМАТИЧЕСКИЕ (в Open Office.org Calc функцию FACT).

3. Для вычисления коэффициентов 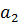, 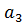ячейку D16 скопировать в E16.

Таким образом, в ячейках C16:F16 вычислены коэффициенты интерполяционного многочлена

, , , ,

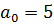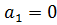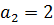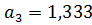
Запишем формулу интерполяционного многочлена:

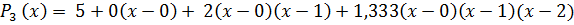
Задание 3. Вычислить значение интерполяционного многочлена при заданном значении x =0,3.

1. В ячейке Н9 вычислить разность 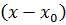; =D5-B9

2. В ячейке Н10 вычислить 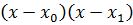: =Н9*($D$5-B10)

3. Ячейку Н10 скопировать в Н11.

4. В ячейку Н12 ввести формулу =C16+МУМНОЖ(D16:F16;H9:H11)

Здесь нужно использовать функцию умножения матриц МУМНОЖ из категории МАТЕМАТИЧЕСКИЕ (в Open Office.org Calc MMULT).

Таблица 3.

Значение интерполяционного многочлена при значении x=0,3 равно 5,056.

Лабораторная работа №2.