Глава 6 Вынужденные механические колебания
Вынужденными колебаниями называют такие колебания, которые возникают в системе при действии на нее внешней вынуждающей периодически изменяющейся силы, называемой вынуждающей.
Характер (зависимость от времени) вынуждающей силы может быть различным. Это может сила, меняющаяся по гармоническому закону. Например, звуковая волна, источником которой является камертон, попадает на барабанную перепонку или мембрану микрофона. На перепонку начинает действовать гармонически меняющаяся сила давления воздуха.
Вынуждающая сила может носить характер толчков или коротких импульсов. Например, взрослый раскачивает ребенка на качелях, периодически толкая их в тот момент, когда качели приходят в одно из крайних положений.
Наша задача – выяснить, как реагирует колебательная система на воздействие периодически изменяющейся вынуждающей силы.
§ 1 Вынуждающая сила изменяется по гармоническому закону
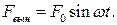 |
При выведении колебательной системы из положения равновесия в ней будут действовать: квазиупругая сила Fх = - kx, сила сопротивления
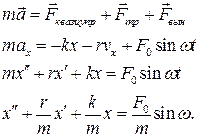 |
Fсопрх = - rvx и вынуждающая сила Fвын = F0sin wt.
Второй закон Ньютона запишется в виде:
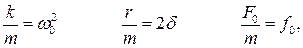 |
Введя обычные обозначения
получим дифференциальное уравнение

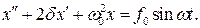 (1)
(1)
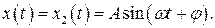 |
Решение уравнения (1) ищут в виде
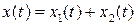 , где
, где 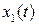 - это решение уравнения (1), если бы в нем не было правой части. Видно, что без правой части уравнение превращается в известное нам уравнение затухающих колебаний, решение которого мы уже знаем. За достаточно большое время свободные колебания, которые возникнут в системе при выведении ее из положения равновесия, практически затухнут, и в решении уравнения останется только второе слагаемое. Будем искать это решение в виде
- это решение уравнения (1), если бы в нем не было правой части. Видно, что без правой части уравнение превращается в известное нам уравнение затухающих колебаний, решение которого мы уже знаем. За достаточно большое время свободные колебания, которые возникнут в системе при выведении ее из положения равновесия, практически затухнут, и в решении уравнения останется только второе слагаемое. Будем искать это решение в виде 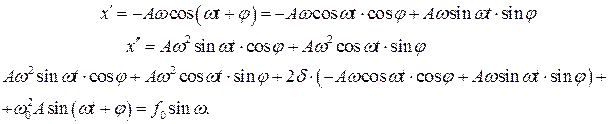 |
Вычисли первую и вторую производную от x(t) и подставим их в уравнение (1):
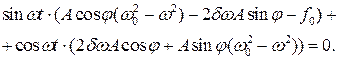 |
Сгруппируем слагаемые иначе:
Это равенство должно выполняться в любой момент времени t, что возможно только, если коэффициенты при синусе и косинусе равны нулю.
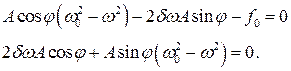 |
Из второго уравнения получаем 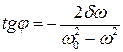 . Этому значению должно удовлетворять j, чтобы x2(t) было решением уравнения (1).
. Этому значению должно удовлетворять j, чтобы x2(t) было решением уравнения (1).
Для определения неизвестного А возведем оба полученных нами уравнения в квадрат и сложим. Решая полученное равенство относительно А, найдем:
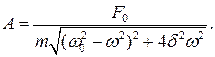 (2)
(2)
Анализ полученного результата:
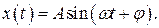 |
Итак,тело, на которое действует вынуждающая сила, меняющаяся по гармоническому закону, совершает колебательное движение с частотой вынуждающей силы.
Разберем подробнее вопрос об амплитуде вынужденных колебаний:
1 Амплитуда установившихся вынужденных колебаний не меняется с течением времени. (Сравните с амплитудой свободных затухающих колебаний).
2 Амплитуда вынужденных колебаний прямо пропорциональна амплитуде вынуждающей силы.
3 Амплитуда зависит от трения в системе (А зависит от d, а коэффициент затухания d, в свою очередь, зависит от коэффициента сопротивления r). Чем больше трение в системе, тем амплитуда вынужденных колебаний меньше.
4 Амплитуда вынужденных колебаний зависит от частоты вынуждающей силы w. Как? Исследуем функцию А(w).
·
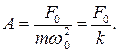 |
При w = 0 (постоянная сила действует на колебательную систему) смещение тела неизменно с течением времени (надо иметь в виду то, что это относится к установившемуся состоянию, когда собственные колебания уже практически затухли).
· При w ® ¥, то, как нетрудно видеть, амплитуда А стремится к нулю.
· Очевидно, что при какой-то частоте вынуждающей силы амплитуда вынужденных колебаний примет наибольшее значение (для данного d). Явление резкого возрастания амплитуды вынужденных колебаний при определенном значении частоты вынуждающей силы носит название механического резонанса.
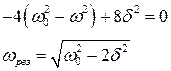 |
Найдем резонансную частоту wрез. Для этого найдем минимум выражения, стоящего под корнем в знаменателе дроби (2). Продифференцировав это выражение по w и приравняв к нулю, получим:
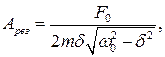 |
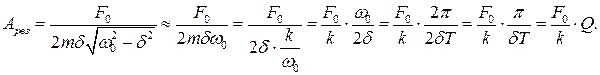 |
Интересно, что добротность колебательной системы в этом случае показывает во сколько раз резонансная амплитуда превышает смещение тела от положения равновесия под действием постоянной силы F0.
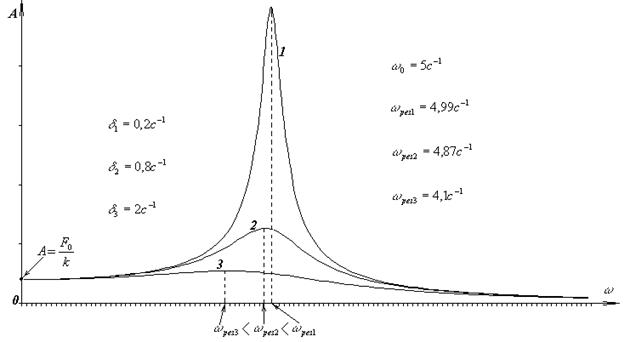
Мы видим, что и резонансная частота, и резонансная амплитуда зависят от коэффициента затухания d. С уменьшением d к нулю резонансная частота возрастает и стремится к частоте собственных колебаний системы w0. При этом резонансная амплитуда возрастает и при d = 0 обращается в бесконечность. Разумеется, на практике амплитуда колебаний бесконечной быть не может, так как в реальных колебательных системах всегда действуют силы сопротивления. Если система имеет малое затухание, то приближенно можно считать, что резонанс наступает при частоте собственных колебаний.:
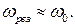 |
При больших значениях коэффициента затухания резонансные явления исчезают. Амплитуда вынужденных колебаний монотонно убывает.
Вернемся к вопросу о фазе вынужденных колебаний.
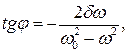 |
где 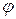 в рассматриваемом случае - это сдвиг по фазе между вынуждающей силой и смещением тела от положения равновесия.
в рассматриваемом случае - это сдвиг по фазе между вынуждающей силой и смещением тела от положения равновесия.
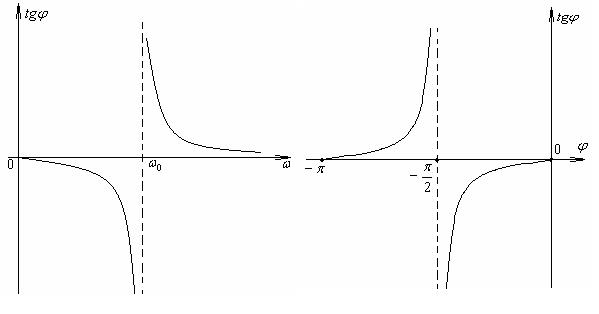 Нетрудно видеть, что сдвиг по фазе между силой и смещением зависит от трения в системе
Нетрудно видеть, что сдвиг по фазе между силой и смещением зависит от трения в системе 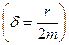 и частоты внешней вынуждающей силы
и частоты внешней вынуждающей силы 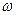 . Эта зависимость показана на рисунке. Видно, что при
. Эта зависимость показана на рисунке. Видно, что при 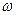 <
< 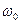 тангенс принимает отрицательные значения, а при
тангенс принимает отрицательные значения, а при 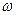 >
> 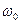 - положительные.
- положительные.
Зная зависимость 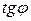 от угла
от угла 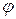 , можно получить зависимость
, можно получить зависимость 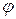 от частоты вынуждающей силы
от частоты вынуждающей силы 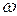 .
.
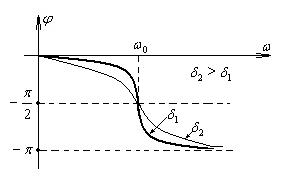
При частотах внешней силы, существенно меньших собственной, смещение отстает по фазе от вынуждающей силы незначительно. При увеличении частоты внешней силы это запаздывание по фазе растет. При резонансе 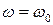 (если
(если 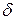 невелико) сдвиг по фазе становится равным
невелико) сдвиг по фазе становится равным 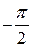 . При
. При 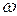 >>
>> 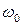 колебания смещения и силы происходят в противофазе. Такая зависимость может показаться на первый взгляд странной. Чтобы понять этот факт, обратимся к энергетическим преобразованиям в процессе вынужденных колебаний.
колебания смещения и силы происходят в противофазе. Такая зависимость может показаться на первый взгляд странной. Чтобы понять этот факт, обратимся к энергетическим преобразованиям в процессе вынужденных колебаний.
§ 2 Энергетические превращения
Как мы уже знаем, амплитуда колебаний определяется полной энергией колебательной системы. Ранее было показано, что амплитуда вынужденных колебаний остается неизменной с течением времени. Это значит, что полная механическая энергия колебательной системы с течением времени не меняется. Почему? Ведь система не замкнута! Две силы - внешняя периодически меняющаяся и сила сопротивления – совершают работу, которая должна менять полную энергию системы.
Попробуем разобраться, в чем дело. Мощность внешней вынуждающей силы может быть найдена следующим образом:
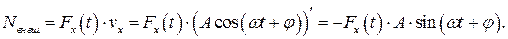
Видим, что мощность внешней силы 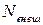 , подпитывающей колебательную систему энергией, пропорциональна амплитуде колебаний
, подпитывающей колебательную систему энергией, пропорциональна амплитуде колебаний 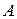 .
.
Счет работы силы сопротивления энергия колебательной системы должна уменьшаться, переходя во внутреннюю. Мощность силы сопротивления:
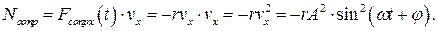
Очевидно, что мощность силы сопротивления 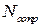 пропорциональна квадрату амплитуды
пропорциональна квадрату амплитуды 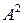 . Изобразим обе зависимости на графике.
. Изобразим обе зависимости на графике.
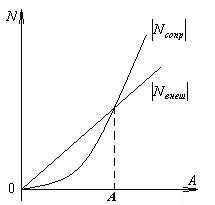
Чтобы колебания были установившимися (амплитуда не менялась с течением времени), работа внешней силы за период должна компенсировать потери энергии системой за счет работы силы сопротивления. Точка пересечения графиков мощностей как раз соответствует этому режиму. Представим, что в силу каких-то причин амплитуда вынужденных колебаний уменьшилась. Это приведет к тому, что мгновенная мощность внешней силы окажется больше мощности потерь. Это приведет к росту энергии колебательной системы, и амплитуда колебаний восстановит прежнее значение.
Аналогичным образом можно убедиться, что при случайном увеличении амплитуды колебаний мощность потерь превысит мощность внешней силы, что приведет к уменьшению энергии системы, и, следовательно, к уменьшению амплитуды.
Вернемся к вопросу о сдвиге по фазе между смещением и вынуждающей силой при резонансе. Мы уже показали, что смещение отстает, а, значит, сила опережает смещение, на 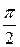 . С другой стороны, проекция скорости в процессе гармонических колебаний всегда опережает координату на
. С другой стороны, проекция скорости в процессе гармонических колебаний всегда опережает координату на 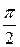 . Это означает, что при резонансе внешняя вынуждающая сила и скорость колеблются в одной фазе. А значит они сонаправлены в любой момент времени! Работа внешней силы в этом случае всегда положительна, она вся идет на пополнение колебательной системы энергией.
. Это означает, что при резонансе внешняя вынуждающая сила и скорость колеблются в одной фазе. А значит они сонаправлены в любой момент времени! Работа внешней силы в этом случае всегда положительна, она вся идет на пополнение колебательной системы энергией.
§ 3 Несинусоидальное периодическое воздействие
Вынужденные колебания осциллятора возможны при любом периодическом внешнем воздействии, а не только синусоидальном. При этом установившиеся колебания, вообще говоря, не будут синусоидальными, но они будут представлять собой периодическое движение с периодом, равным периоду внешнего воздействия.
Внешнее воздействие 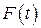 может представлять собой, например, последовательные толчки (вспомните, как взрослый человек «раскачивает» ребенка, сидящего на качелях). Если период внешних толчков совпадает с периодом собственных колебаний, то в системе может наступать резонанс. Колебания при этом будут почти синусоидальными. Сообщаемая системе при каждом толчке энергия идет пополнение полной энергии системы, теряемой за счет трения. Понятно, что при этом возможны варианты: если сообщаемая при толчке энергия равна или превышает потери на трение за период, то колебания будут либо установившимися, либо их размах будет возрастать. Это хорошо видно на фазовой диаграмме.
может представлять собой, например, последовательные толчки (вспомните, как взрослый человек «раскачивает» ребенка, сидящего на качелях). Если период внешних толчков совпадает с периодом собственных колебаний, то в системе может наступать резонанс. Колебания при этом будут почти синусоидальными. Сообщаемая системе при каждом толчке энергия идет пополнение полной энергии системы, теряемой за счет трения. Понятно, что при этом возможны варианты: если сообщаемая при толчке энергия равна или превышает потери на трение за период, то колебания будут либо установившимися, либо их размах будет возрастать. Это хорошо видно на фазовой диаграмме.
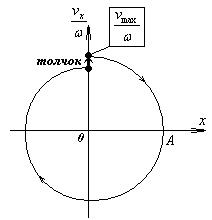 Очевидно, что резонанс возможен и в том случае, когда период следования толчков будет кратен периоду собственных колебаний. Такое невозможно при синусоидальном характере внешнего воздействия.
Очевидно, что резонанс возможен и в том случае, когда период следования толчков будет кратен периоду собственных колебаний. Такое невозможно при синусоидальном характере внешнего воздействия.
С другой стороны, даже при совпадении частоты толчков с собственной частотой резонанс может не наблюдаться. Если только потери на трение за период превышают энергию, полученную системой во время толчка, то полная энергия системы будет уменьшаться, а колебания будут затухать.
§ 4 Параметрический резонанс
Внешнее воздействие на колебательную систему может сводиться к периодическому изменению параметров самой колебательной системы. Возбуждаемые таким образом колебания называются параметрическими, а сам механизм – параметрическим резонансом.
Прежде всего, попытаемся ответить на вопрос: можно ли раскачать уже имеющиеся в системе малые колебания, периодически изменяя определенным образом какой-либо ее параметр.
В качестве примера рассмотрим раскачивание человека на качелях. Сгибая и выпрямляя ноги в «нужные» моменты, он фактически изменяет длину маятника. В крайних положениях человек приседает, тем самым чуть-чуть опускает центр тяжести колебательной системы, в среднем положении человек выпрямляется, поднимая центр тяжести системы.
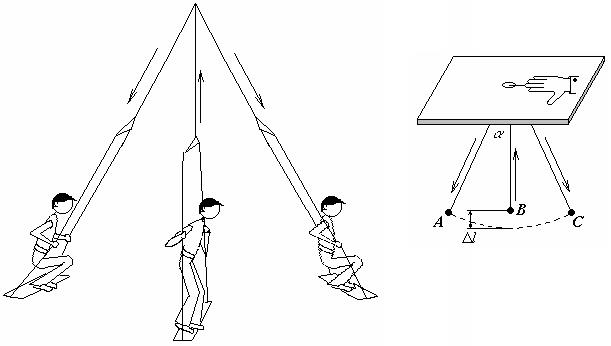
Чтобы понять, почему при этом человек раскачивается, рассмотрим предельно упрощенную модель человека на качелях – обычный небольшой маятник, то есть небольшой грузик на легкой и длинной нити. Чтобы имитировать поднимание и опускание центра тяжести, пропустим верхний конец нити через маленькое отверстие и будем вытягивать нить в те моменты, когда маятник проходит положение равновесия, и настолько же опускать нить, когда маятник проходит крайнее положение.
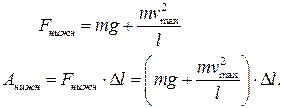 |
Подтягивая маятник в нижней точке траектории, мы совершаем положительную работу
В крайнем положении
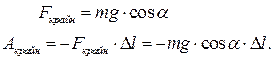 |
Работа силы натяжения нити за период (с учетом того, что подъем груза и его опускание производится два раза за период и что Dl << l):
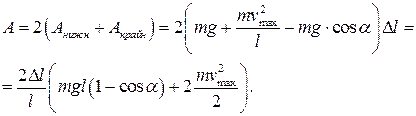 |
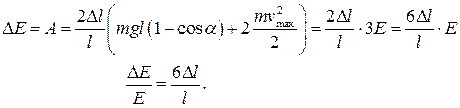 |
Обратите внимание, что в скобках стоит не что иное, как утроенная энергия колебательной системы. Кстати, это величина положительная, следовательно, работа силы натяжения (наша работа) положительная, она приводит к увеличению полной энергии системы, а значит, к раскачке маятника.
Интересно, что относительное изменение энергии за период не зависит от того, слабо раскачивается маятник или сильно. Это очень важно, и вот почему. Если маятник «не подкачивать» энергией, то за каждый период он будет терять за счет силы трения определенную часть своей энергии, и колебания будут затухать. А чтобы размах колебаний увеличивался, необходимо, чтобы приобретаемая энергия превышала потерянную на преодоление трения. И это условие, оказывается, одно и то же – как при маленькой амплитуде, так и при большой.
Например, если за один период энергия свободных колебаний уменьшается на 6%, то для того, чтобы колебания маятника длиной 1 м не затухали, достаточно в среднем положении уменьшать его длину на 1 см, а в крайнем – на столько же увеличивать.
Возвращаясь к качелям: если вы начали раскачиваться, то нет необходимости приседать все глубже и глубже – приседайте все время одинаково, и будете взлетать все выше и выше!
*** Опять добротность!
Как мы уже сказали, для параметрической раскачки колебаний необходимо выполнение условия DЕ > Атрения за период.
Найдем работу силы трения за период
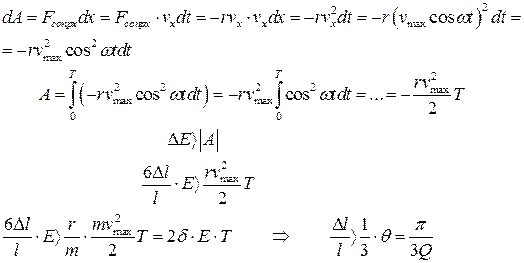 |
Видно, что относительная величина подъема маятника для его раскачки определяется добротностью системы.
§ 5 Значение резонанса
Вынужденные колебания и резонанс широко используются в технике, особенно в акустике, электротехнике, радиотехнике. Резонанс, в первую очередь, используется тогда, когда из большого набора колебаний разной частоты хотят выделить колебания определенной частоты. Резонанс используется и при изучении очень слабых периодически повторяющихся величин.
Однако, в ряде случаев резонанс – нежелательное явление, так как может привести к большим деформациям и разрушениям конструкций.
§ 6 Примеры решения задач
Задача 1 Вынужденные колебания пружинного маятника под действием внешней синусоидальной силы.
К пружине жесткостью k = 10 Н/м подвесили груз массой m = 10 г и поместили систему в вязкую среду с коэффициентом сопротивления r = 0,1 кг/с. Сравните собственную и резонансную частоту системы. Определите амплитуду колебаний маятника при резонансе под действием синусоидальной силы с амплитудой F0 = 20 мН.
Решение:
1 Собственная частота колебательной системы – это частота свободных колебаний в отсутствии трения. Собственная циклическая частота равна 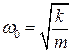 , частота колебаний
, частота колебаний 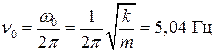 .
.
2 Резонансная частота – это частота внешней вынуждающей силы, при которой амплитуда вынужденных колебаний резко возрастает. Резонансная циклическая частота равна 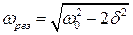 , где
, где 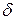 - коэффициент затухания, равный
- коэффициент затухания, равный 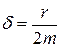 .
.
Таким образом, резонансная частота равна 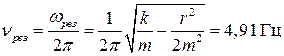 . Нетрудно видеть, что резонансная частота меньше собственной! Также видно, что чем меньше трение в системе (r) , тем ближе резонансная частота к собственной.
. Нетрудно видеть, что резонансная частота меньше собственной! Также видно, что чем меньше трение в системе (r) , тем ближе резонансная частота к собственной.
3 Резонансная амплитуда равна
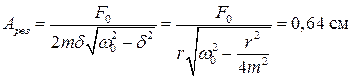 .
.
Задача 2 Резонансная амплитуда и добротность колебательной системы
К пружине жесткостью k = 10 Н/м подвесили груз массой m = 100 г и поместили систему в вязкую среду с коэффициентом сопротивления
r = 0,02 кг/с. Определите добротность колебательной системы и амплитуду колебаний маятника при резонансе под действием синусоидальной силы с амплитудой F0 = 10 мН. Найдите отношение резонансной амплитуды к статическому смещению под действием постоянной силы F0 = 20 мН и сравните это отношение с добротностью.
Решение:
1 Добротность колебательной системы равна 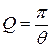 , где
, где 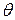 - логарифмический декремент затухания.
- логарифмический декремент затухания.
Логарифмический декремент затухания равен 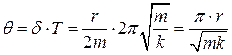 .
.
Находим добротность колебательной системы 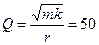 .
.
2 Резонансная амплитуда равна
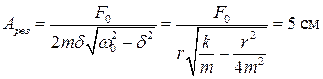 .
.
3 Статическое смещение под действием постоянной силы F0 = 10 мН равно 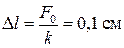 .
.
4 Отношение резонансной амплитуды к статическому смещению под действием постоянной силы F0 равно
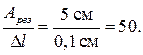
Нетрудно видеть, что это отношение совпадает с добротностью колебательной системы 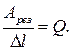
Задача 3 Резонансные колебания балки
Под действием веса электромотора консольная бака, на которой он установлен, прогнулась на 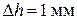 . При каком числе оборотов якоря мотора может возникнуть опасность резонанса?
. При каком числе оборотов якоря мотора может возникнуть опасность резонанса?
Решение:
1 Корпус двигателя и балка, на которой он установлен, испытывают периодические толчки со стороны вращающегося якоря мотора и, следовательно, совершают вынужденные колебания с частотой следования толчков.
Резонанс будет наблюдаться при совпадении частоты следования толчков с собственной частотой колебания балки с мотором 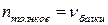 . Необходимо найти собственную частоту колебаний системы балка – мотор.
. Необходимо найти собственную частоту колебаний системы балка – мотор.
2 Аналогом колебательной системы балка – мотор может служить вертикальный пружинный маятник, масса которого равна массе мотора. Собственная частота 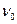 колебаний пружинного маятника равна
колебаний пружинного маятника равна 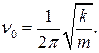 . Но жесткость пружины и масса мотора не известны! Как быть?
. Но жесткость пружины и масса мотора не известны! Как быть?
3 В положении равновесия пружинного маятника сила тяжести груза уравновешивается силой упругости пружины 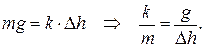
4 Находим вращения якоря двигателя, т.е. частоту следования толчков
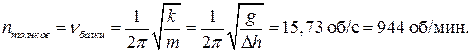
Задача 4 Вынужденные колебания пружинного маятника под действием периодических толчков.
Гиря массой m = 0,5 кг подвешена к спиральной пружине жесткостью k = 20 Н/м. Логарифмический декремент затухания колебательной системы равен 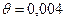 . Гирю хотят раскачать короткими толчками, действуя на гирю силой F = 100 мН в течение времени τ = 0,01 с. Какой должна быть частота следования ударов, чтобы амплитуда гири была наибольшей? В какие моменты и в каком направлении следует толкать гирю? До какой амплитуды удастся раскачать гирю таким способом?
. Гирю хотят раскачать короткими толчками, действуя на гирю силой F = 100 мН в течение времени τ = 0,01 с. Какой должна быть частота следования ударов, чтобы амплитуда гири была наибольшей? В какие моменты и в каком направлении следует толкать гирю? До какой амплитуды удастся раскачать гирю таким способом?
Решение:
1 Вынужденные колебания могут происходить при любом периодическом воздействии. При этом установившееся колебание будет происходить с частотой следования внешнего воздействия. Если период внешних толчков совпадает с частотой собственных колебаний, то в системе наступает резонанс – амплитуда колебаний становится наибольшей. В нашем случае для наступления резонанса период следования толчков должен совпасть с периодом колебаний пружинного маятника.
Логарифмический декремент затухания мал, следовательно, мало трение в системе, и период колебаний маятника в вязкой среде практически совпадает с периодом колебаний маятника в вакууме:
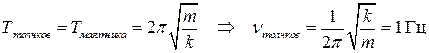 .
.
2 Очевидно, направление толчков должно совпадать со скоростью гири. В этом случае работа внешней силы, пополняющей систему энергией, будет положительной. И колебания будут раскачиваться. Энергия, получаемая системой в процессе удара
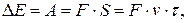
будет наибольшей при прохождении грузом положения равновесия, ибо в этом положении скорость маятника максимальна.
Итак, наиболее быстро система раскачается при действии толчков в направлении движения груза при прохождении им положения равновесия.
3 Амплитуда колебаний прекращает расти, когда энергия, сообщаемая системе в процессе удара, будет равна потерям энергии на трение за период: 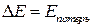 .
.
Энергию потерь за период найдем через добротность колебательной системы
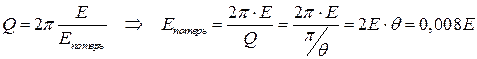 ,
,
где Е – полная энергия колебательной системы, которая может быть рассчитана как 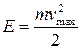 .
.
Подставляем вместо энергии потерь энергию, получаемую системой в процессе удара:
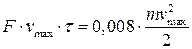 .
.
Максимальная скорость в процессе колебаний равна 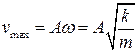 . С учетом этого получаем
. С учетом этого получаем 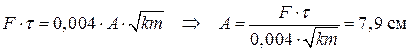 .
.
§7 Задания для самостоятельного решения
Тест «Вынужденные колебания»
1 Какие колебания называются вынужденными?
А) Колебания, происходящие под действием внешних периодически изменяющихся сил;
Б) Колебания, возникающие в системе после внешнего толчка;
2 Какие из перечисленных колебаний является вынужденным?
А) Колебание груза, подвешенного к пружине, после однократного его отклонения от положения равновесия;
Б) Колебание диффузора громкоговорителя во время работы приемника;
В) Колебание груза, подвешенного к пружине, после однократного удара по грузу в положении равновесия;
Г) Вибрация корпуса электрического двигателя в процессе его работы;
Д) Колебания барабанной перепонки человека, слушающего музыку.
3 На колебательную систему с собственной частотой 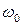 действует внешняя вынуждающая сила, меняющаяся по закону
действует внешняя вынуждающая сила, меняющаяся по закону 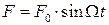 . Коэффициент затухания в колебательной системе равен
. Коэффициент затухания в колебательной системе равен 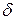 . По какому закону изменяется координата тела с течением времени?
. По какому закону изменяется координата тела с течением времени?
А) 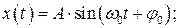 Б)
Б) 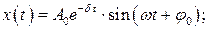
В) 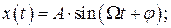 Г)
Г) 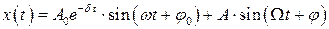 .
.
4 На колебательную систему действует внешняя вынуждающая сила, меняющаяся по закону 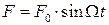 . Амплитуда внешней силы
. Амплитуда внешней силы 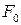 неизменна с течением времени. Как меняется амплитуда вынужденных колебаний, когда собственные колебания, возникшие в системе в момент начала действия внешней силы, прекратились?
неизменна с течением времени. Как меняется амплитуда вынужденных колебаний, когда собственные колебания, возникшие в системе в момент начала действия внешней силы, прекратились?
А) Амплитуда вынужденных колебаний будет уменьшаться, так как система будет непрерывно терять энергию за счет работы силы трения;
Б) Амплитуда вынужденных колебаний будет увеличиваться, поскольку энергия системы будет непрерывно возрастать за счет работы внешней вынуждающей силы;
В) Амплитуда вынужденных колебаний будет оставаться неизменной, так как потери энергии системой на трение будут восполняться прибылью энергии за счет работы внешней вынуждающей силы.
5 Система совершает вынужденные колебания под действием синусоидальной силы. Укажите все факторы, от которых зависит амплитуда этих колебаний.
А) От амплитуды внешней вынуждающей силы;
Б) Наличия у колебательной системы энергии в момент начала действия внешней силы;
В) Параметров самой колебательной системы;
Г) Трения в колебательной системе;
Д) Существования в системе собственных колебаний в момент начала действия внешней силы;
Е) Времени установления колебаний;
Ж) Частоты внешней вынуждающей силы.
6 Брусок массой m совершает вынужденные гармонические колебания по горизонтальной плоскости с периодом T и амплитудой A. Коэффициент трения μ. Какую работу совершает внешняя вынуждающая сила за время, равное периоду T?
А) 4μmgA; Б) 2μmgA; В) μmgA; Г) 0;
Д) Ответ дать не возможно, так как не известна величина внешней вынуждающей силы.
7 Составьте правильное утверждение
Резонансом называется явление…
А) Совпадения частоты внешней силы с собственной частотой колебательной системы;
Б) Резкое возрастание амплитуды вынужденных колебаний.
Резонанс наблюдается при условии
А) Уменьшении трения в колебательной системе;
Б) Увеличении амплитуды внешней вынуждающей силы;
В) Совпадении частоты внешней силы с собственной частотой колебательной системы;
Г) При совпадении частоты внешней силы с резонансной частотой.
8 Явление резонанса может наблюдаться в…
А) В любой колебательной системе;
Б) В системе, совершающей свободные колебания;
В) В автоколебательной системе;
Г) В системе, совершающей вынужденные колебания.
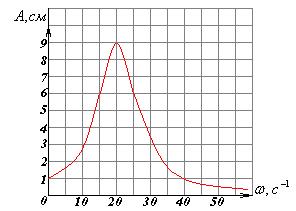 9 На рисунке представлен график зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы. Резонанс наступает на частоте…
9 На рисунке представлен график зависимости амплитуды вынужденных колебаний от частоты вынуждающей силы. Резонанс наступает на частоте…
А) 0 Гц;
Б) 20 Гц;
В) 125,6 Гц;
Г) 3,2 Гц.
10 Три одинаковых маятника, находящиеся в различных вязких средах, совершают вынужденные колебания. На рисунке показаны резонансные кривые для этих маятников. Какой из маятников испытывает наибольшее сопротивление со стороны вязкой среды в процессе колебаний?
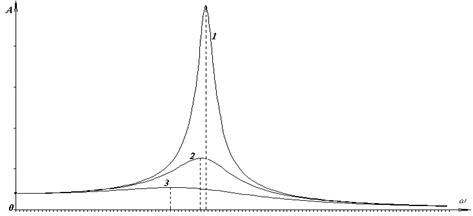
А) 1; Б) 2; В) 3;
Г) Ответ дать не возможно, поскольку амплитуда вынужденных колебаний кроме частоты внешней силы зависит еще и от ее амплитуды. Об амплитуде внешней вынуждающей силы в условии ничего не говорится.
11 Период собственных колебаний колебательной системы равен Т0. Каким может быть период следования толчков, чтобы амплитуда колебаний резко увеличилась, то есть в системе возник резонанс?
А) Т0; Б) Т0, 2 Т0, 3 Т0,…;
В) Раскачать качели можно толчками любой частоты.
12 Ваш младший брат сидит на качелях, вы раскачиваете его кратковременными толчками. Каким должен быть период следования толчков, чтобы процесс происходил наиболее эффективно? Период собственных колебаний качелей Т0.
А) 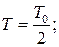 Б)
Б) 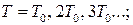 В)
В) 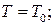
Г) Раскачать качели можно толчками любой частоты.
13 Ваш младший брат сидит на качелях, вы раскачиваете его кратковременными толчками. В каком положении качелей следует производить толчок и в каком направлении толкать, чтобы процесс происходил наиболее эффективно?
А) Толкать в крайнем верхнем положении качелей в направлении положения равновесия;
Б) Толкать в крайнем верхнем положении качелей в направлении от положения равновесия;
В) Толкать в положении равновесия в направлении движения качелей;
Г) Толкать можно в любом положении, но обязательно в направлении движения качелей.
14 Казалось бы, стреляя из рогатки в мост в такт его собственным колебаниям и сделав очень много выстрелов, его можно сильно раскачать, однако это вряд ли удастся. Почему?
А) Масса моста (его инертность) велика по сравнению с массой «пули» из рогатки, мост не сможет прийти в движение под действием таких ударов;
Б) Сила удара «пули» из рогатки настолько мала что, мост не сможет прийти в движение под действием таких ударов;
В) Энергия, сообщаемая мосту за один удар много меньше потерь энергии на трение за период.
15 Вы несете ведро с водой. Вода в ведре раскачивается и выплескивается. Что можно сделать, чтобы этого не происходило?
А) Размахивать рукой, в которой находится ведро, в такт с ходьбой;
Б) Изменить скорость движения, оставив неизменной длину шагов;
В) Периодически останавливаться и ждать, когда колебания воды успокоятся;
Г) Следить за тем, чтобы в процессе движения рука с ведром располагалась строго вертикально.
Задачи
1 Система совершает затухающие колебания с частотой 1000 Гц. Определите частоту v0 собственных колебаний, если резонансная частота
998 Гц.
2 Определите, на какую величину Dv резонансная частота отличается от собственной частоты v0 = 1000 Гц колебательной системы, характеризующейся коэффициентом затухания d = 400с-1.
3 Груз массы 100 г, подвешенный на пружине жесткости 10 Н/м, совершает вынужденные колебания в вязкой среде с коэффициентом сопротивления r = 0,02 кг/с. Определите коэффициент затухания, резонансную частоту и амплитуду. Амплитудное значение вынуждающей силы 10 мН.
4 Амплитуды вынужденных гармонических колебаний при частотах w1 = 400 с-1 и w2 = 600 с-1 равны между собой. Определите резонансную частоту.
5 Грузовики въезжают по грунтовой дороге на зерновой склад с одной стороны, разгружаются и выезжают со склада с той же скоростью, но с другой стороны. С какой стороны склада выбоины на дороге идут чаще, чем с другой? Как по состоянию дороги определить, с какой стороны склада въезд, а какой выезд? Ответ обосновать
