Среднеквадратическое отклонение. Правило 3-сигма

Среднеквадратическое отклонение вычисляется как квадратный корень из выборочной или исправленной дисперсии:

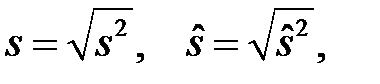(3.9)

где s² и 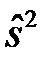вычисляются по формулам (3.5) – (3.8).

В программе Excel среднеквадратическое отклонение (называется стандартное отклонение) вычисляется с помощью функций СТАНДОТКЛОН() и СТАНДОТКЛОНП(). При этом СТАНДОТКЛОНП() соответствует выборочной дисперсии, т.е. значению s, а СТАНДОТКЛОН() отвечает значению 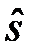(квадратного корня из исправленной дисперсии).

Пример 3.3. Найти выборочную и исправленную дисперсии для выборки из 10 значений, записанных в диапазоне В2:В11 (рис.3.2).

Решение. В ячейку В12 введите формулу =ДИСП(B2:B11), а в ячейку В13 — формулу =ДИСПР(B2:B11).

Для контроля введем в ячейку С12 формулу

=СУММКВ(B2:B11)/9-10*СРЗНАЧ(B2:B11)^2/9

а в ячейку С13 — формулу

=СУММКВ(B2:B11)/10-СРЗНАЧ(B2:B11)^2

Мы увидим, что функция ДИСП() вычисляет исправленную дисперсию, а ДИСПР() — выборочную.

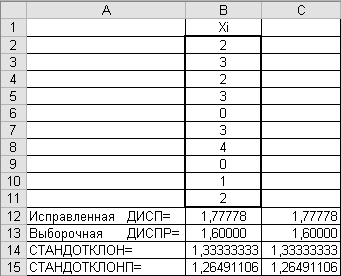
Рис.3.2

Введите в ячейку В14 формулу

=СТАНДОТКЛОН(B2:B11),

а в ячейку В15 — формулу

=СТАНДОТКЛОНП(B2:B11).

Для контроля введите в ячейку С14 формулу =КОРЕНЬ(B12), а в ячейку С15 — формулу =КОРЕНЬ(B13).

Мы видим, что функция СТАНДОТКЛОНП() соответствует квадратному корню из выборочной дисперсии, а СТАНДОТКЛОН() отвечает значению квадратного корня из исправленной дисперсии.

Правило «3-сигма» применяется для приближенной проверки гипотезы о том, что выборка соответствует генеральной совокупности с нормальным законом распределения и выводится из следующего факта. Для нормальной случайной величины с математическим ожиданием a и среднеквадратическим отклонением σ вероятность попадания в интервал (a – 3σ, a + 3σ) равна 0,997. Это следует из формулы (1.7):

.

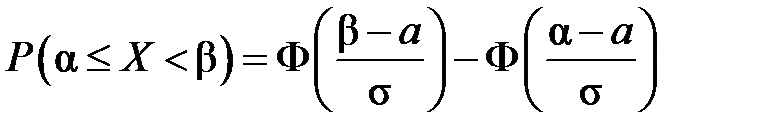В нашем случае α = a – 3σ, β = a + 3σ. По формуле (1.7) имеем

.

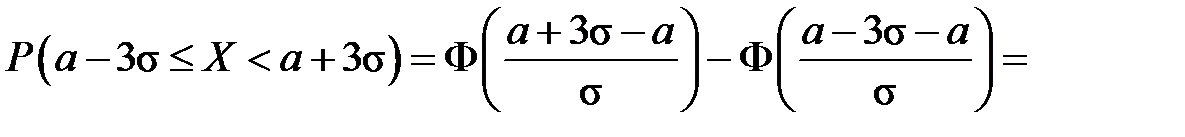
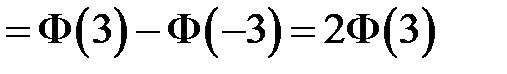Значение функции Лапласа можно найти по таблице или с помощью формулы в Excel. Введите в любой ячейке формулу =НОРМСТРАСП(3)-0,5. Получим значение 0,498650102, умножив это значение на 2, получим приближенно 0,997.

Правило «3-сигма».Если «почти все» элементы выборки попадают в интервал 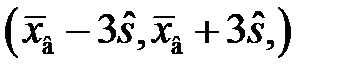, где 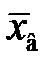выборочное среднее, а 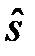стандартное отклонение, то генеральная совокупность имеет нормальное распределение.

1.4. Общая, межгрупповая и внутригрупповая дисперсии.
Правило сложения дисперсий

Пусть выборочные данные представлены в виде k групп (верхние индексы обозначают принадлежность группе, а не возведение в степень!):

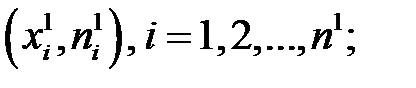— первая группа, объем равен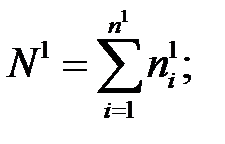

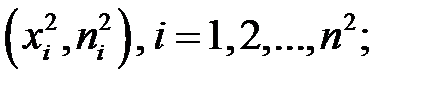— вторая группа, объем равен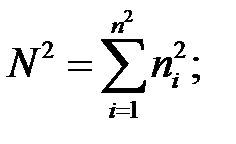

…

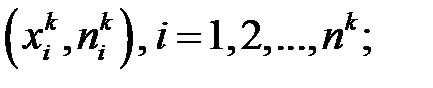— k-ягруппа, объем равен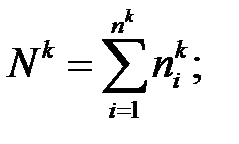

Общий объем выборки равен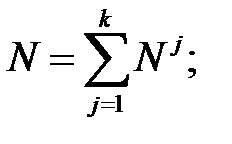

Тогда можно вычислитьобщую, межгрупповую и внутригрупповую дис­персии в следующем порядке.

Групповые средние 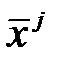и групповые дисперсии 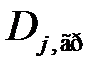вычисляются по формулам:

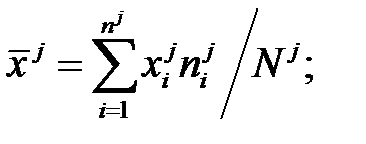
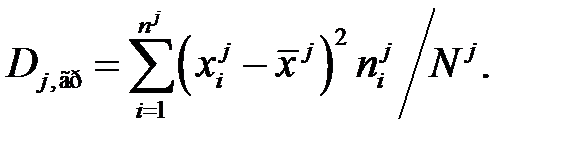(3.10)

Внутригрупповой дисперсией называется взвешенная средняя групповых дисперсий:

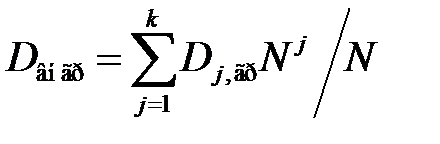. (3.11)

Внутригрупповая дисперсия отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки.

Общая средняя и общая дисперсия вычисляются по формулам:

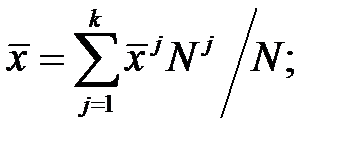
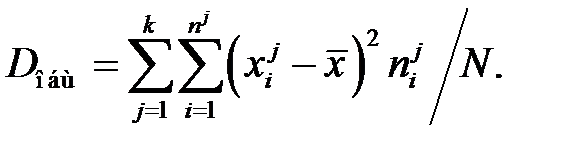(3.12)

Общая дисперсия измеряет вариацию признака во всей совокупности под влиянием всех факторов, обусловливающих эту вариацию.

Межгрупповая дисперсия вычисляется по формуле:

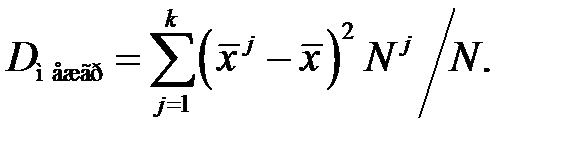(3.14)

Межгрупповая дисперсия характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки.

Существует закон, связывающий три вида дисперсий:

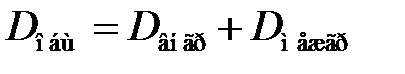(3.15)

Данное соотношение называютправилом сложения диспер­сий.Согласно этому правилу общая дисперсия, возникающая под влиянием всех факторов, равна сумме дисперсий, возникающих под влиянием всех прочих факторов, и дисперсии, возникающей за счет группировочного признака.

Зная любые два вида дисперсий, можно определить или про­верить правильность расчета третьего вида.

Для демонстрации равенства (3.15) рассмотрим следующий пример.

Пример 3.4. Определить групповые средние, групповые дисперсии, среднюю из груп­повых дисперсий (внутригрупповую дисперсию), межгрупповую дисперсию, общую дисперсию по данным табл. 3.1, в которой приведены данные о производительности труда трех бригад рабочих-токарей за десять дней работы (за каждый день приведено среднее число изготовленных за час деталей на одного рабочего и число работавших в этот день рабочих в бригаде).

Дать толкование полученным результатам.

Таблица 3.1

Дни	1-я бригада	Число работавших	2-я бригада	Число работавших	3-я бригада	Число работавших

Решение. Введите данные в программе Excel в ячейках A1:D11, как показано на рис.3.3.

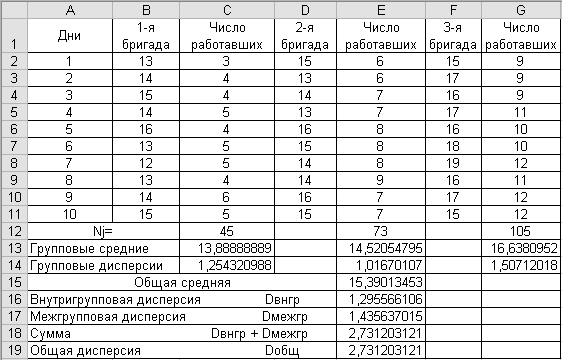
Рис. 3.3

Объедините следующие группы ячеек: А12:В12, А13:В13, А14:В14, А15:D15, А16:D16, А17:D17, А18:D18, А19:D19 и впишите в них тексты, как показано на рис. 3.3.

В ячейках С12, Е12, G12 просуммируйте соответствующие столбцы с помощью значка «Автосумма» или введите в эти ячейки формулы:

=СУММ(C2:C11), =СУММ(E2:E11), =СУММ(G2:G11).

В ячейку С13 введите формулу

=СУММПРОИЗВ(B2:B11;C2:C11)/СУММ(C2:C11)

Выделите ячейку С13 и маркером заполнения протяните вправо до ячейки G13, а затем удалите в ячейках D13, F13 содержимое с помощью клавиши «Delete». В ячейках E13, G13 должны получиться формулы:

=СУММПРОИЗВ(D2:D11;E2:E11)/СУММ(E2:E11),

=СУММПРОИЗВ(F2:F11;G2:G11)/СУММ(G2:G11).

В ячейки С14, Е14, G14 для вычисления групповых дисперсий введите, соответственно, формулы:

=СУММПРОИЗВ((B2:B11-C13)^2;C2:C11)/C12,

=СУММПРОИЗВ((D2:D11-E13)^2;E2:E11)/E12,

=СУММПРОИЗВ((F2:F11-G13)^2;G2:G11)/G12.

Для вычисления общей средней в ячейку Е15 введите формулу:

=(C13*C12+E13*E12+G13*G12)/(C12+E12+G12).

Для вычисления внутригрупповой дисперсии в ячейку Е16 введите формулу:

=(C14*C12+E14*E12+G14*G12)/(C12+E12+G12).

Для вычисления межгрупповой дисперсии в ячейку Е17 введите формулу:

=((C13-E15)^2*C12+(E13-E15)^2*E12

+(G13-E15)^2*G12)/(C12+E12+G12)

Для вычисления суммы межгрупповой и внутригрупповой дисперсий в ячейку Е18 введите формулу =E16+E17.

Для вычисления общей дисперсии в ячейку Е19 введите формулу:

=(СУММПРОИЗВ((B2:B11-E15)^2;C2:C11)

+СУММПРОИЗВ((D2:D11-E15)^2;E2:E11)

+СУММПРОИЗВ((F2:F11-E15)^2;G2:G11))/(C12+E12+G12).

Результаты вычислений приведены на рис. 3.3. как видим, равенство (3.15) выполняется.

Дадим теперь толкование полученным результатам.

Средняя производительность на одного рабочего за десять дней составляет

в первой бригаде 13,89 деталей в час,

во второй бригаде — 14,52 детали в час,

в третьей бригаде — 16,64 деталей в час.

Средняя производительность на одного рабочего (по всему цеху) за десять дней составляет 15,39 деталей в час.

Межгрупповая дисперсия, равная 1,44, характеризует систематическую вариацию, т. е. различия в величине изучаемого признака, возникающие под влиянием признака-фактора, положенного в основание группировки, т.е., в данном случае, принадлежность определенной бригаде.

Внутригрупповая дисперсия равна 1,29 и отражает случайную вариацию, т. е. часть вариации, происходящую под влиянием неучтенных факторов, другими словами, остаточную дисперсию.

Общая дисперсия составляет 2,73.