Расчет параметров уравнения регрессии по индивидуальным данным

Рассмотрим расчет параметров уравнения регрессии между стоимостью основных фондов х и валовым выпуском продукции у.

Исходные данные и расчет приведем в табл. 2.

Предположим, что зависимость между показателями х и у линейная, т.е.

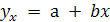
Таблица 2

Расчетная таблица для определения параметров уравнения регрессии

по индивидуальным данным

Основные фонды, млн руб. х	Валовой выпуск продукции, млн руб. у	х2	ху	_ ух = -10,24 + + 2,12х
∑x = 520	∑у = 1000	∑x²=35624	∑ух=70244	∑ух=1000

Параметры а и b этого уравнения найдем, решив систему нормальных уравнений (5). Подставив в нее необходимые суммы, рассчитанные в табл. 2, получим

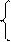10a + 520b = 1000,

520 a + 35624b = 70244.

Решив систему уравнений, найдем, что а = -10,24, b = 2,12. Отсюда искомое уравнение регрессии у по х будет

y_x = -10,24 + 2,12 х .

Подставляя в данное уравнение последовательно значения х (12, 16, 25 и т.д.), находим теоретические (выравненные) значения результативного признака, т.е. y_x, которые показывают, каким теоретически должен быть средний объем валового выпуска продукции при данной стоимости основных фондов х_i (при прочих равных условиях для всех предприятий). Теоретические значения y_x приведены в последней графе табл. 2 (с округлением до целых).

Для нахождения а и b при линейной зависимости могут быть предложены готовые формулы.

Так, на основе определителей 2-го порядка из системы нормальных уравнений (5) получим:

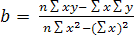, (6)

или, разделив каждое уравнение на n в системе нормальных уравнений (12), и путем дальнейших преобразований получим:

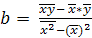(7)

или

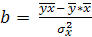(8)

следовательно,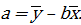

В рассматриваемом примере найдем параметр b по формуле

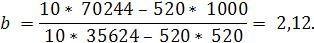
Рассчитав 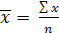= 520/10 = 52 и у = 1000 / 10 = 100, легко найти а:

а =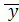

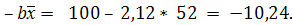
Параметр b, т.е. коэффициент при х, в уравнении линейной регрессии называется коэффициентом регрессии.

Коэффициент регрессии показывает, на сколько (в абсолютном выражении) изменяется значение результативного признака у при изменении факторного признака х на единицу.

По данным корреляционной таблицы необходимо рассчитать линейный коэффициент корреляции по формуле

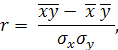
где σ_х и σ_у – соответственно среднее квадратическое отклонение в ряду х и в ряду у.

,

.

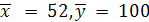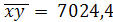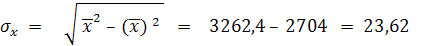
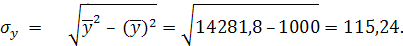
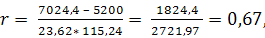
т.е. между х и у связь выше средней.

r < 0,3 – малая зависимость;

0,3 < r <0,6 - средняя зависимость;

0,6 < r <0,8 - зависимость выше средней;

r > 0,8 – большая, сильная зависимость.

Эмпирическая линия регрессии, отражающая на графике зависимость между х и у, не всегда дает основание для выдвижения гипотезы о линейной зависимости. Характер ломаной линии может быть различным.