Спектр синусоїдного сигналу
Спектральний аналіз – це знаходження усіх гармонійних складових з відповідними частотами, які входять до складу даного сигналу і в підсумку відтворюють його.
Дискретне перетворення Фур’є (ДПФ) дозволяє визначити спектр дискретизованого, обмеженого по тривалості сигналу, який зафіксований своїми вибірковими (дискретними) значеннями.
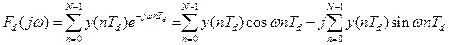 (2.2.1)
(2.2.1)
Спектр, який є дискретним(поданий у певних частотах у вигляді решітчастої функції, коли на відповідних частотах подаються лінії відповідних амплітуд – лінії спектру). Будуючи комплексні величини ( маючи Re і Im) спектр може бути поданий у експоненціальній формі коли амплітуда експоненти зветься амплітудно-частотною характеристикою(або амплітудним спектром), а фаза експоненти(комплексний спектр) – фазово-частотною характеристикою(або фазовим спектром).
Спектр, для обмеження по тривалості функції задається на інтервалі частот, який дорівнює частоті дискретизації часового сигналу.
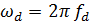
(2.2.2)
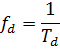
(2.2.3)
Поданий на інтервалі, що дорівнює частоті дискретизації числом своїх дискрет (ліній спектру), яке рівне N. N – число точок дискретизації.
Крок подачі ліній спектру визначається, як різниця між двома сусідніми частинами ліній спектру.
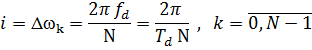 (2.2.4)
(2.2.4)
Амплітуда часового сигналу на 0-ій частоті:
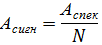
Амплітуда ліній спектру на інших частотах:
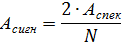
У цьому випадку сигнал 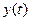 буде таким:
буде таким:
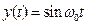 (2.2.5)
(2.2.5)
і може бути поданий з використанням формул Ейлера як різниця експоненціальних функцій, тобто як
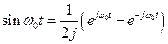 (2.2.6)
(2.2.6)
а ДПФ обох функцій в (2.2.6) вираховується окремо для кожної з них. Для першої складової в (2.2.6) спектр визначається згідно з виразом (1.6.11), а для другої складової рівняння отримуємо із тих же міркувань, але як зміщену ліворуч функцію, тобто:
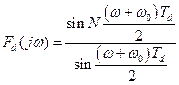 (2.2.7)
(2.2.7)
Таким чином, спектр синусоїди, вибірки якої подані у межах прямокутного вікна, визначається як різниця рівнянь (1.6.11) та (2.2.7):
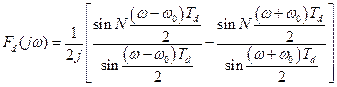 (2.2.8)
(2.2.8)
і яке знову дає обвідну дискретного спектру. Амплітуди ліній спектру визначаються двома способами:
1) із рівняння (2.2.8) розраховують обвідну і далі з кроком 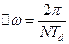 по ній будують окремі лінії спектру;
по ній будують окремі лінії спектру;
2) обвідна ігнорується, а розрахунки безпосередньо виконуються по формулі для ДПФ при конкретних значеннях 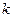 :
:
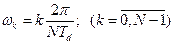
Розрахунки
Завдання №1:
1. Враховуючи вираз для поліному 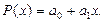 запишемо суму квадратів відхилень як:
запишемо суму квадратів відхилень як:
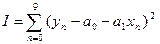
2. Знайдемо значення коефіцієнтів при яких значення цього квадратичного відхилення було б мінімальним:
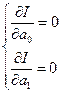
3. Підставивши у цю систему вираз для I і знайшовши відповідні похідні отримаємо наступну систему:
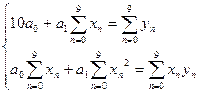
4. Зробимо заміну:
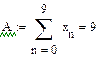 |
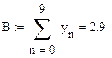 |
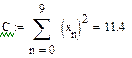 |
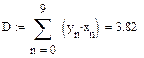 |
Тоді наша система матиме вигляд:
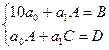
5. Підставивши ці значення у систему, отримаємо
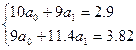
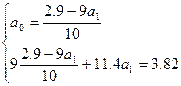
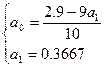
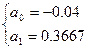
6. Отримаємо згладжуючий поліном:
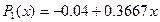
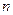 | ||||||||||
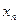 | 0,2 | 0.4 | 0.6 | 0.8 | 1.2 | 1.4 | 1.6 | 1.8 | ||
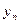 | -0.8 | -0.6 | 0.2 | 0.7 | 0.9 | 1.4 | 0.8 | 0.4 | 0.1 | -0.2 |
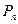 | -0.04 | 0.033 | 0.107 | 0.18 | 0.253 | 0.327 | 0.4 | 0.473 | 0.547 | 0.62 |
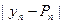 | 0.76 | 0.633 | 0.093 | 0.52 | 0.647 | 1.073 | 0.4 | 0.073 | 0.447 | 0.82 |
Максимальне значення абсолютної похибки:
Max( 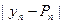 )=1.073
)=1.073
Квадратичне відхилення при цьому:
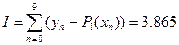
Графік заданої ( 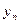 ) та апроксимованої функцій (Р(n))
) та апроксимованої функцій (Р(n)) 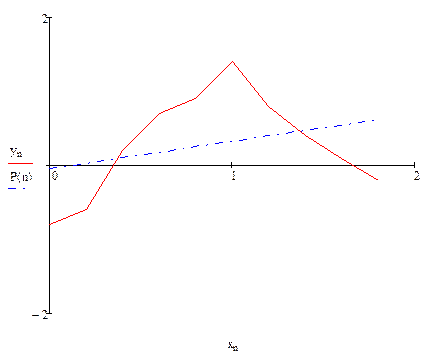
Завдання №2
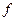 гц гц | …. | …. | … | … | … | |||||||||
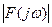 | ||||||||||||||
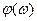 град град | -180 | -90 | -90 | -180 |
Амплітуда сигналу на 0-ій частоті вираховується згідно з наступним співвідношенням: 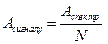
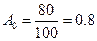
Амплітуда сигналу на інших частотах вираховується в згідно з наступним співвідношенням: 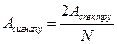
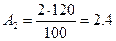
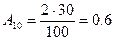
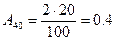
Так як для 2 складової наявний повтори з від’ємної області частот з тією ж амплітудою і фазою, і оскільки значення фази головних складових -180, то робимо висновок, що це є косинусоїда зі знаком «-».
Так як для 10 складової наявний повтор з від’ємної області частот з тією ж амплітудою, але протилежною фазою, і оскільки значення фази головних складових 90, то робимо висновок, що це є синусоїди зі знаком «-».
Так як для 40 складової наявний повтор з від’ємної області частот з тією ж амплітудою, але протилежною фазою, і оскільки значення фази головних складових -90, то робимо висновок, що це є синусоїди зі знаком «+».
Запишемо аналітичний вираз для часового сигналу 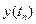 ;
; 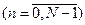 з урахуванням фазової складової спектру:
з урахуванням фазової складової спектру:
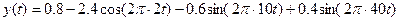
Частота дискретизації – 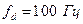
Період дискретизації – 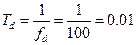
Кількість дискрет– 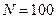
Інтервал визначення – 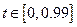
Графічна інтерпретація заданого спектру:
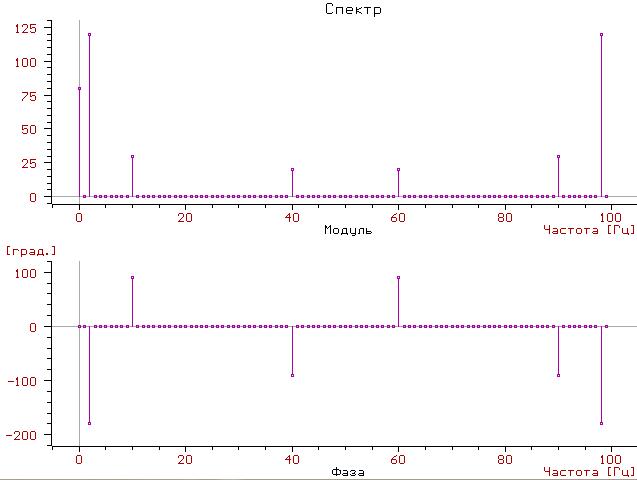
Висновки
1. Було проведено згладжування даних за допомогою полінома 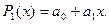 Ми отримали згладжуючий поліном:
Ми отримали згладжуючий поліном: 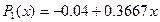 Максимальне значення абсолютної похибки: 1.073. Квадратичне відхилення при цьому:
Максимальне значення абсолютної похибки: 1.073. Квадратичне відхилення при цьому: 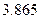 . Проте як бачимо згладження поліномом 1 степені є не ефективним, так як він не відтворює гармонічні складові сигналу (поліном першої степені – пряма лінія).
. Проте як бачимо згладження поліномом 1 степені є не ефективним, так як він не відтворює гармонічні складові сигналу (поліном першої степені – пряма лінія).
2.Було проведено відновлення дискретизованого часового сигналу
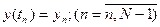 по його заданому спектру. Записано аналітичний вираз сигналу:
по його заданому спектру. Записано аналітичний вираз сигналу:
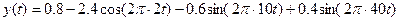 . Побудовано графік спектру.
. Побудовано графік спектру.
