Определение.Совокупность объектов, количественный или качественный признак которой требуется изучить статистическими методами, называют генеральной совокупностью

Математическая статистика

Цели работы: овладение различными методами обработки статистических данных. Нахождение точечных и интервальных характеристик вариационного ряда. Овладение методом составления доверительных интервалов для оценки математического ожидания нормального распределения при известном s и для оценки среднего квадратического отклонения s нормального распределения. Овладение методами установления связи между двумя случайными величинами X и Y при большом числе наблюдений и методами определения параметров выборочного уравнения прямой линии регрессии по сгруппированным данным.

Основные теоретические положения

Вариационный ряд и его числовые характеристики

Математическая статистика– раздел прикладной математики, занимающийся установлением закономерностей, которым подчинены массовые случайные явления, на основе данных наблюдений и измерений.

Определение.Совокупность объектов, количественный или качественный признак которой требуется изучить статистическими методами, называют генеральной совокупностью.

Определение. Выборкой (выборочной совокупностью) называют совокупность объектов, случайно отобранных из генеральной совокупности.

Определение. Объемом совокупности (выборочной или генеральной) называют число элементов этой совокупности.

Определение.Последовательность наблюдаемых значений 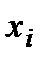называют вариационным рядом.

Определение.Число наблюдений 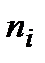значения признака 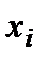называют частотой значения .

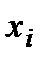Определение.Отношение частоты 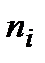к объему выборки 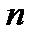называют относительной частотой значения : .

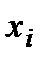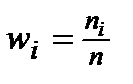Определение. Вариационный ряд называют дискретным, если два любых соседних наблюдаемых значения отличаются на постоянную величину.

Определение. Вариационный ряд называют интервальным (непрерывным), если его соседние наблюдаемые значения могут отличаться на сколь угодно малую величину.

Определение. Накопленной частотой 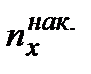называют величину, показывающую, сколько наблюдалось значений признака, меньших числа 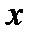. Отношение накопленной частоты к общему числу наблюдений называют накопленной относительной частотой .

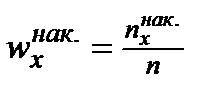Определение. Эмпирической функцией распределения (функцией распределения выборки) называют функцию .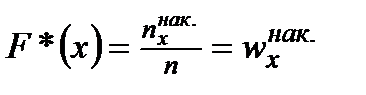

Определение. Кумулятивной кривой (кумулятой) называют ломаную, соединяющую точки 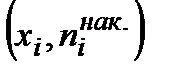или .

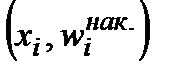Определение. Полигоном частот (относительных частот) называют ломаную, отрезки которой последовательно соединяют точки 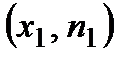, , 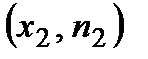…, 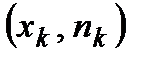(соответственно точки , , …, ).

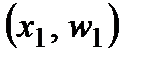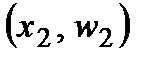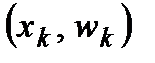Определение. Гистограммой частот (относительных частот) называют ступенчатую фигуру, состоящую из прямоугольников, основаниями которых служат частичные интервалы длиной 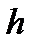, а высоты равны отношению 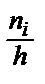(соответственно 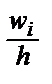), где длина 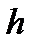выбирается из практических соображений, а 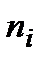равна сумме частот наблюдаемых значений, попавших в 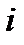-й интервал.

Определение. Размахом вариации называют разность между наибольшим и наименьшим значениями вариационного ряда: .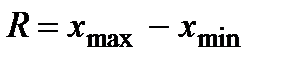

Длина интервала 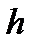вычисляется по формуле 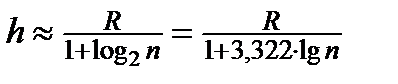. Число промежутков гистограммы равно 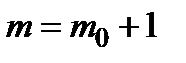, где 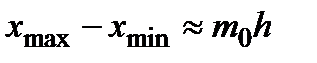. За значение левого конца первого промежутка принимают 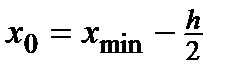, за значение правого конца 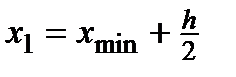. Все остальные значения концов промежутков получаются по формуле , .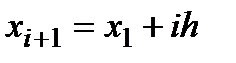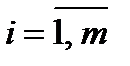