П 2.1. Конденсированное состояние. Кинематика и динамика жидкостей

Жидкость – агрегатное состояние вещества, промежуточное между твердым и газообразным состояниями.

Чистые жидкости по химическому составу – однокомпонентные жидкости.

Жидкие смеси (растворы) по химическому составу – двух–или многокомпонентные жидкости.

Нормальные (обычные) жидкости – однородные макроскопические и изотропные жидкости. При отсутствии внешних воздействий обладают только одной жидкой фазой.

Квантовые жидкости– жидкости, которые могут находиться в нормальной и одной или нескольких анизотропных фазах.

Простые жидкости– жидкости, состоящие из сферически симметричных молекул, между которыми действуют силы Ван дер Ваальса, не имеющие какого-либо преимущественного направления и обладающие наиболее простыми свойствами.

Ближний порядок – упорядоченное расположение по отношению к любой молекуле ближайших к ней соседей.

Зависимость между временемtодного колебания молекулы относительно данного положения и временем "оседлой" жизниt₀:

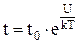
где U – «потенциальный барьер», численно равный разности энергий молекулы в двух возможных областях ее колебаний, разделяющий две возможные области колебаний молекулы);

Т – температура жидкости;

k – постоянная Больцмана.

Число молекул жидкости в некотором сферическом слое толщинойdrна расстоянииrот произвольно выбранной молекулы:

,

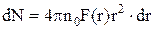где n₀=N/V – число молекул в единице объема жидкости;

F(r) – радиальная функция распределения, которая определяет вероятность нахождения некоторой молекулы жидкости в какой-либо точке ее объема.

Вязкость – свойство жидкостей оказывать сопротивление перемещению одной их части относительно другой. Определяется их молекулярным составом и строением.

Основной закон вязкого течения (закон Ньютона):

,

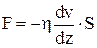где dv/dz – градиент скорости в направлении z;

S – площадь слоя, по которому происходит сдвиг;

h – коэффициент динамической вязкости, который характеризует сопротивление жидкости смещению ее слоев.

Зависимость коэффициента вязкости жидкостей от температуры:

,

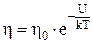где U – энергия, необходимая для перехода молекулы жидкости из одного равновесного состояния в другое.

Кинематическая вязкость– отношение динамической вязкости к плотности жидкости:

n=h/r.

Текучесть жидкостей– свойство, обратное вязкости, обусловлено той свободой движения молекул в объеме, которая еще допускается силами сцепления между ними.

Коэффициент текучести (или текучесть):

j=1/h.

Сжимаемость– способность жидкости изменять свой объем под действием всестороннего давления.

Коэффициент сжимаемости – выражает уменьшение единичного объема (или плотности) при увеличении давления на единицу:

,

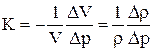где DV, Dρ – изменение первоначального объема и первоначальной плотности жидкости при изменении давления на Dp.

Уравнение состояния жидкости (с определенной степенью точности):

.

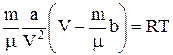Сфера действия молекулярных сил – область, в которой расположены взаимодействующие молекулы, в центре которой находится рассматриваемая молекула (R~10^{-9 м).}

Экспериментальный закон зависимости объема жидкости от температуры:

V_t=V₀(1+at),

где a – коэффициент объемного расширения, который определяется соотношением:

.

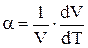Связь коэффициентов сжимаемости и объемного расширения жидкостей:

.

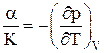Поверхностное натяжение – мера некомпенсированности межмолекулярных сил в поверхностном (межфазном) слое.

Работа dA по изменению поверхности жидкости наdS совершается за счет изменения потенциальной энергии поверхностного слоя (поверхностной энергии жидкости) dW_ps:

dA=-dW_ps=-s×dS,

где «минус» показывает, что увеличение поверхности жидкости сопровождается совершением работы;

s – коэффициент поверхностного натяжения, который характеризует свойства поверхности жидкости и показывает, какую работу необходимо совершить, чтобы увеличить поверхность жидкости на единицу.

Работа по изменению поверхности жидкости, совершаемая внешними силами:

dA=–F×dx=-s×dS=-sℓ×dx,

где ℓ – длина контура, охватывающего поверхность жидкости;

dx – смещение границы поверхностного слоя;

F – сила поверхностного натяжения;

s – коэффициент поверхностного натяжения, который численно равен силе поверхностного натяжения, стремящейся изменить длину контура, охватывающего поверхность жидкости, на единицу.

Зависимость коэффициента поверхностного натяжения от температуры:

,

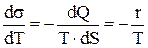где r=dQ/dS – количество тепла, затраченное на изменение поверхности пленки на единицу.

Полное молекулярное давление в поверхностном слое жидкости:

p=p₀±Dp,

где p₀ – молекулярное давление жидкости с плоской поверхностью;

Dp – дополнительное давление, возникающее за счет кривизны поверхности жидкости;

знак «+» – соответствует выпуклой поверхности;

знак «-» – соответствует вогнутой поверхности.

Формула Лапласа для дополнительного давления (для капли, которая полностью заполнена жидкостью, или для пузырька внутри жидкости) в случае:

1) произвольной поверхности

,

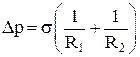где R₁ и R₂ – радиусы кривизны поверхностного слоя жидкости;

Сферической поверхности

,

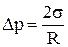где R – радиус сферы;