Тема 1.1.4 Декартово произведение множеств(1ч.)

Запишем с пом. цифр 3 и 5 че­тыре двузначных числа: 35, 53, 33 и 55. Несмотря на то что числа 35 и 53 записаны с помощью одних и тех же цифр, эти числа различные. В том случае, когда важен порядок следова­ния элементов, в математике говорят об упорядоченных на­борах элементов. В рассмотренном примере мы имели дело с упорядоченными парами.

Упорядоченную пару, образованную из элементов а и Ь, принято записывать, используя круглые скобки: {а; Ь). Эле­мент а называют первой координатой (компонентой) пары, а элемент b второй координатой (компонентой) пары.

Определение. Декартовым произведением множеств А и В называется множество всех пар, первая компонента ко­торых принадлежит множеству А, а вторая компонента принадлежит множеству В.

Декартово произведение множеств А и В обозначают А х В. Используя это обозначение, определение декартова произведе­ния можно записать так:

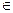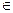АхВ= {(х; у) | х А и у В}.

Операцию нахождения декартова произведения множеств называют декартовым умножением.

Рассмотрим два одинаковых мн-ва А={3,5}, тогда АхА={(3;3),(3;5),(5;3),(5;5)}

Примечание:

Можно изобразить декартово произведение множеств :

1) при помощи графа или таблицы. Например, декартово произведение множеств А = {1, 2, 3} и В = {3,5} можно представить так, как показано на рисунке :

2) Декартово произведение двух числовых множеств (конеч­ных и бесконечных) :

А) А = {1, 2, 3} и В= {3, 5} на координатной плоскости будет выглядеть так, как показано на рисунке:

Заметим, что элементы множест­ва А мы изобразили на оси Ох, а элементы множества В - на оси Оу.

Декартово произведение представлено точками.

б) ) А = {1, 2, 3} и В= [3, 5]

Решение, а) Так как множество А состоит из трех элемен­тов, а множество В содержит все действительные числа от 3 до 5, включая и сами эти числа, то декар­тово произведение А х В будет со­стоять из бесконечного множества пар, первая компонента которых либо 1, либо 2, либо 3, а вторая -любое действительное число из про­межутка [3, 5]. Такое множество пар действительных чисел на коорди­натной плоскости изобразится тремя отрезками

В) бесконечны оба множества А=[1, 3] и В=[3, 5] тогда АхВ это все, что внутри квадрата, т.е. этот квадрат (его нужно заштриховать):

Г) А=RиВ=R,т.е. на мн-ве действительных чисел. То АхВ это вся координатная плоскость.

Д) А=R и В=[3, 5], то АхВ– полоса. (рис.)

Упражнения

1. Перечислите элементы декартова произведения А хВ, если:

а)А = {a, b,c,d},B= {b,k,l}

д)А=В= {а, Ь, с};

ъ)А = {а,Ь,с},В = 0.

2.Изобразите в прямоугольной системе координат мно­жество Ах В, если:

а) А = [-2, 2], В ={2, 3,4};

2. Изобразите в прямоугольной системе координат декартово произведение множеств и , если

1)

2)