Методика изучения сложения и вычитания в пределах 10
Место изучения темы: 1 класс
Цели:
- Обеспечить усвоение детьми рациональных вычислительных приемов сложения и вычитания;
- Сформировать прочные вычислительные навыки;
- Научить решать простые задачи на сложение и вычитание различных видов ( нахождение суммы, остатка, увеличение и уменьшение числа на несколько единиц, разностное сравнение, нахождение неизвестного слагаемого )
Задачи:
- Знакомство с вычислительными приемами и формирование умения применять их при составлении таблиц сложения и вычитания.
- Заучивание таблиц сложения и вычитания в тесной связи с усвоением состава числа в пределах 10. Формирование навыков сложения.
Наглядные пособия и дидактический материал
1) Таблица классная настенная с названиями чисел при сложении и вычитании вида:
| слагаемое | слагаемое | сумма | ||
| + | = |
2) Набор подвижных цифр и знаков
3) Набор геометрических фигур различных видов и разного цвета
4) Набор карточек с числовыми фигурами, иллюстрирующими числа 1-5
5) Наборы предметных картинок для составления задач
Содержание и особенности изучения темы
Сложение и вычитание в пределах 10 составляют основу выполнения устных и письменных вычислений за пределами первого десятка.
Конкретный смысл сложения и вычитания осознается детьми в процессе действий с множествами предметов и находит применение при решении задач. Сложение рассматривается как объединение множеств, не имеющих общих элементов. Вычитание - как удаление части множества. Сложение связывается с увеличением числа элементов данного множества; вычитание – с уменьшением числа элементов данного множества.
Значительное место в этой теме отводится знакомству с названиями компонентов и результатов действий и осознанию связей между ними, а также усвоению свойств арифметических действий.
Включаются также элементы алгебры и геометрии: дети знакомятся с математическими выражениями (сумма, разность ), учатся их читать и записывать, приступают к сравнению выражений, на основе чего получают числовые равенства и неравенства вида: 4+2>7, 7-3<7+3, 3+2=2+3. Здесь же учащиеся знакомятся с уравнениями вида x-3=7, 5+x=9 и учатся их решать. Закрепляются умения чертить и измерять отрезки, включаются задачи на составление геометрических фигур из заданных, и на вычленение знакомых геометрических фигур из данной фигуры.
Изучение сложения вычитания в пределах 10 проводится по такому плану:
1. Подготовительный этап: раскрытие конкретного смысла действий сложения и вычитания, запись и чтение примеров, случаи прибавить и вычесть 1, где результаты находятся на основе знания свойства натурального ряда чисел (когда к числу прибавляем 1, получаем число, следующее за ним при счете, а когда вычитаем из числа 1, то получаем предыдущее число).
2. Изучение приемов присчитывания и отсчитывания по одному и группами для случаев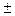 
2, 3, 4.
3. Изучение приема перестановки слагаемых для случаев + 5, 6, 7, 8, 9. Таблица сложения и состав чисел из слагаемых.
4. изучение приема вычитания на основе знания связи между суммой и слагаемыми для случаев – 5,6, 7, 8, 9.
Подготовительная работа к изучению сложения и вычитания начинается с первых уроков рассмотрения нумерации. Выполняя многократно операции над множествами, дети уясняют, что операции объединения соответствует действие сложения, а операции удаления части множества – действие вычитания. Также обращается внимание детей на то, что, когда прибавляют, то становится больше, чем было; когда вычитают, становится меньше.
К концу изучения нумерации учащиеся должны прочно усвоить способы образования любого числа первого десятка присчитыванием и отсчитыванием единицы, и используя этот прием ( а не пересчитывание ), свободно выполнять сложение и вычитание с единицей. Постепенно дети обобщают свои выводы и формулируют выводы: прибавить 1 числу - значит назвать следующее за ним число; вычесть 1 из числа – значит назвать предшествующее ему число. На специально отведенном уроке приводят в систему все случаи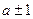 
, под руководством учителя дети составляют таблицы «прибавить 1» и «вычесть 1» и затем заучивают их наизусть.
На втором этапе рассматриваются случаи сложения и вычитания вида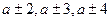 
, результаты которых находят присчитыванием или отсчитыванием по частям.
Работа над вычислительными навыками строится по такому плану:
1) подготовительные упражнения;
2) знакомство с приемами вычисления;
3) закрепление знания приемов, выработка вычислительного навыка;
4) составление и заучивание таблиц.
Рассмотрим методику ознакомления с вычислительным приемом «прибавить и вычесть 2».
На подготовительном этапе дети учатся решать примеры в два действия 2+1+1, 9-1-1, чтобы закрепить умения прибавлять и вычитать единицу и накопить наблюдения: если прибавим (вычтем) 1 и еще 1, то всего прибавим (вычтем) 2.
На уроке по ознакомлению с новыми приемами вычислений учитель ставит цель перед детьми – научиться прибавлять и вычитать число 2. Решение первых примеров выполняется с опорой на предметное действие. Решается пример 4+2. Пусть эти букеты на окне изображают число 4, а эти 2 букета на столе – число 2. Покажите как2 букета присоединить к тем 4 (ученик переносит цветы на окно: сначала один букет, затем второй).Запишем то, что сделал Вова. Сколько сначала к 4 прибавили? Сколько получилось? Как же можно прибавить 2 к 4? Чтобы прибавить 2 к 4, надо прибавить сначала 1 к 4, получится 5, а потом прибавить к 5 еще 1, получится 6.
На доске запись:
4 + 2 = 6
4 + 1 = 5
5 + 1 = 6
Далее ученики выполняют задание: рисуют в тетради 7 яблок, затем 2 яблока раскрашивают, записывают пример 7-2 и, опираясь на свою практическую работу (сначала раскрасили 1, а потом еще 1 яблоко), объясняют, как вычесть 2.
В таком же плане рассматриваются еще несколько заданий, затем переходят к решению примеров с пояснением приемов вычислений.
С помощью аналогичных упражнений раскрываются приемы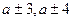 
. Приемы вычислений также иллюстрируют действиями с предметами и на первых порах несколько примеров решают с подробной записью на доске
| 4 + 3 = 7 | 9 – 3 = 6 | |||
| 4 + 2 = 6 | 9 – 1 = 8 | |||
| 6 + 1 = 7 | 8 – 2 = 6 |
Для приемов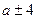 
запись может быть такой же, но целесообразнее начать записывать по-другому: 5 + 4 = 5 + 2 + 2 = 9, 10 – 4 = 10 – 2 - 2 = 6.
Вначале примеры решаются с подробными пояснениями вслух, постепенно пояснения сокращаются, затем проговариваются кратко про себя. С целью выработки навыков включаются устные упражнения ( устный счет, игры «молчанка», «эстафета», «лесенка», «круговые примеры» ). Очень полезны арифметические диктанты. Особенно полезны творческие упражнения: составить задачи, примеры, исправить неверно решенные примеры, вставить пропущенное число или знак действия - 3 = 7, 8 - = 6, 8 + = 10; 6 * 4 = 10, 6 * 4 = 2.
Эффективными для формирования вычислительных навыков являются упражнения с равенствами и неравенствами: сравнить выражения и вставить знаки: 7 + 2 * 7, 10 – 3 * 4; проверить, правильно ли поставлены знаки: 6 + 4<10, 6 +3>10,8 +2 =10; вставить подходящее число, чтобы получилось верная запись: 10 – 4<, 5 + 2>, 5 + 3=.
Сравнение выражений выполняют на основе сравнения их значений, поэтому дети с помощью таких упражнений закрепляют навыки вычислений.
Завершает работу над каждым из приемов 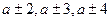составление и заучивание таблиц. Часть каждой таблицы составляется коллективно под руководством учителя, часть – самостоятельно. Одновременно с таблицами сложения и вычитания полезно составить таблиц состава чисел из слагаемых, например:
| 2 + 2 = 4 | 4 = 2 + 2 | 4 – 2 = 2 | ||||
| 3 + 2 = 5 | 5 = 3 + 2 | 5 – 2 = 3 | ||||
| 4 + 2 = 6 | 6 = 4 + 2 | 6 – 2 = 4 | ||||
| … | … | … | ||||
| 8 + 2 = 10 | 10 = 8 + 2 | 10 – 2 = 8 |
На этом этапе учащиеся знакомятся с терминами сложение, вычитание, слагаемое, сумма, а позднее с терминами – уменьшаемое, вычитаемое, разность.
На третьем этапе изучают прием сложения для случаев «прибавить 5, 6, 7, 8, 9». Если при вычислениях применить перестановку слагаемых, то все эти случаи сведутся к ранее изученным видам а + 1, а + 2, а + 3, а + 4. Для этого знакомятся с переместительным свойством сложения.
Раскрыть прием перестановки слагаемых, т. е. показать, когда именно в вычислениях используют переместительное свойство можно при решении практической задачи. Например, надо сложить вместе 2 мешка и 7 мешков муки, стоящие порознь. Как удобнее это сделать: принести 2 мешка к 7 или 7 мешков к двум? На основе таких упражнений дети приходят к выводу: легче к большему числу прибавить меньшее, а переставлять числа всегда можно – сумма от этого не изменится.
Затем показывают, как использовать прием перестановки слагаемых при решении примеров и задач на сложение в пределах 10. После этого составляется таблица сложения в пределах 10. Дети сами могут пояснить, почему включены только эти случаи и почему не включены остальные.
На четвертом этапе изучается прием вычитания, основанный на связи между суммой и слагаемыми для нахождения результатов в случаях «вычесть 5, 6, 7, 8, 9». Взаимосвязь между суммой и слагаемыми рассматривается в теме «Нахождение неизвестного слагаемого». Оперируя с конкретными предметными множествами (демонстрационные и индивидуальные средства наглядности), учащиеся самостоятельно приходят к выводу: если из суммы двух слагаемых вычесть одно слагаемое, то получим другое слагаемое (индуктивный метод: неполная индукция).
В ходе работы над темой дети знакомятся с задачами на увеличение (уменьшение) числа, связанными со сравнением двух множеств предметов. Они должны осознать, что означают выражения «во втором на 2 больше (меньше), чем в первом», научиться сводить задачи этого вида к задачам на нахождение суммы и остатка на основе рассуждения: «На 2 больше, значит, столько же и еще 2», «На 3 меньше, значит, столько же без 3».
В процессе изучения сложения и вычитания продолжается формирование понятия числа нуль. Выполняя действия над множествами, учащиеся постепенно усваивают, что число нуль – это характеристика пустого множества. В конце работы над темой включаются случаи сложения и вычитания с нулем 6 + 0, 6 – 0.