Развитие понятия числа, числовые множества
ИКТИБ ИТА ЮФУ
КУРС ЛЕКЦИЙ ПО МАТЕМАТИКЕ
Глава 1 Комплексные числа
Лекция 1 Комплексные числа (часть 1)
Что мы узнаем на этой лекции
Какие бывают числа? Что такое натуральное число, рациональное число, действительное число, иррациональное число, трансцендентное число? Все ли операции над числами возможны в каждом из этих случаев?
Что такое комплексное число? Операции над числами входят в определение комплексного числа? Как найти сопряженное комплексное число, что такое сложение, вычитание, умножение, деление комплексных чисел? Геометрический смысл операций сложения, вычитания комплексных чисел, умножения комплексных чисел на действительное число. Комплексные числа как векторы на комплексной плоскости.
Как определяется модуль и аргумент комплексного числа? Мы узнаем, в чем заключается геометрический смысл умножения и деления комплексных чисел.
Развитие понятия числа, числовые множества
Рассмотрим множество 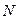 натуральных чисел, т. е. числа
натуральных чисел, т. е. числа 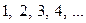 . Для них операции сложения и умножения дают в результате снова натуральные числа. Нам знакомы свойства этих операций:
. Для них операции сложения и умножения дают в результате снова натуральные числа. Нам знакомы свойства этих операций: 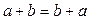 ,
, 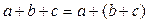 ,
, 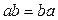 ,
, 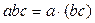 ,
, 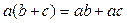 ,
, 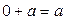 ,
, 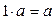 . Также для этих чисел можно ввести операцию возведения в натуральную степень
. Также для этих чисел можно ввести операцию возведения в натуральную степень 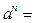
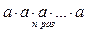 , при этом справедливы соотношения
, при этом справедливы соотношения 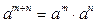 ,
, 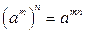 ,
, 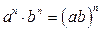 . Попытка ввести обратные операции приводит нас к необходимости расширения понятия числа. Для множества
. Попытка ввести обратные операции приводит нас к необходимости расширения понятия числа. Для множества 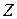 целых чисел, т.е. для чисел
целых чисел, т.е. для чисел 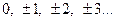 доступно вычитание чисел, обратное их сложению. А попытка ввести операцию деления чисел, обратную к операции умножения, приводит к дальнейшему развитию понятия числа, а именно, к введению рациональных чисел.
доступно вычитание чисел, обратное их сложению. А попытка ввести операцию деления чисел, обратную к операции умножения, приводит к дальнейшему развитию понятия числа, а именно, к введению рациональных чисел.
Рациональными называются числа вида 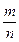 , где
, где 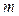 является целым числом (
является целым числом ( 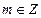 ), а
), а 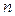 – натуральное число (
– натуральное число ( 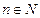 ). Множество рациональных чисел принято обозначать буквой
). Множество рациональных чисел принято обозначать буквой 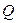 . Рациональные числа содержат в себе целые числа, их можно понимать как корни уравнения
. Рациональные числа содержат в себе целые числа, их можно понимать как корни уравнения 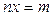 .
.
Дальнейшее развитие понятия числа можно воспринимать как решение все более сложных уравнений. Например, в школьном учебнике доказывается, что уравнение 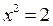 не имеет решение среди рациональных чисел. Конечные и бесконечные десятичные дроби (множество всех точек числовой оси) образуют множество действительных чисел
не имеет решение среди рациональных чисел. Конечные и бесконечные десятичные дроби (множество всех точек числовой оси) образуют множество действительных чисел 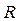 . Действительные числа, не являющиеся рациональными, называются иррациональными числами. Как мы видим, иррациональные числа существуют, например, это любой корень уравнения
. Действительные числа, не являющиеся рациональными, называются иррациональными числами. Как мы видим, иррациональные числа существуют, например, это любой корень уравнения 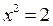 .
.
Отметим еще одно понятие – трансцендентное число. Это иррациональные числа, которые не являются корнями алгебраического уравнения с целыми коэффициентами. Таких чисел подавляющее большинство на числовой оси. Поэтому, как правило, мировые константы являются трансцендентными числами.
