Дифференциал функции и его геометрический смысл
Дифференциалом функции 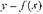 в
в 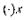 называется главная, линейная относительно
называется главная, линейная относительно 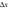 , часть приращения функции.
, часть приращения функции. 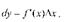
Покажем, что 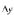 и
и 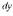 эквивалентные бесконечно малые при
эквивалентные бесконечно малые при 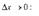
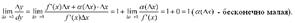
Геометрический смысл дифференциала:
Проведем к графику функции 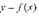 в точку
в точку 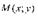 касательную
касательную 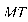 и рассмотрим ординату этой касательной для точки
и рассмотрим ординату этой касательной для точки 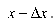 На рисунке
На рисунке 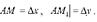 Из прямоугольного треугольника
Из прямоугольного треугольника 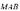 имеем:
имеем: 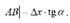 Но, согласно геометрическому смыслу производной,
Но, согласно геометрическому смыслу производной, 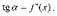 Поэтому
Поэтому 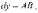 Это означает, что дифференциал функции
Это означает, что дифференциал функции 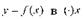 равен приращению ординаты касательной к графику функции в этой точке, когда
равен приращению ординаты касательной к графику функции в этой точке, когда 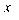 получает приращение
получает приращение 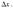
Применение дифференциала в приближённых вычислениях.
Пусть нам известно значение функции y0=f(x0) и ее производной y0' = f '(x0) в точке x0. Покажем, как найти значение функции в некоторой близкой точке x.
Как мы уже выяснили приращение функции Δyможно представить в виде суммы Δy=dy+α·Δx, т.е. приращение функции отличается от дифференциала на величину бесконечно малую. Поэтому, пренебрегая при малых Δx вторым слагаемым в приближенных вычислениях, иногда пользуются приближенным равенством Δy≈dyили Δy»f'(x0)·Δx.
Т.к., по определению, Δy = f(x) – f(x0), то f(x) – f(x0)≈f'(x0)·Δx.
Откуда
f(x) ≈ f(x0) + f'(x0)·Δx
Инвариантность формы первого дифференциала
Если x - независимая переменная, то dx = x - x0 (фиксированное приращение). В этом случае имеемdf (x0) = f'(x0)dx. (3)
Если x = φ(t) - дифференцируемая функция, то dx = φ'(t0)dt. Следовательно,
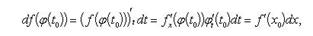 т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.
т. е. первый дифференциал обладает свойством инвариантности относительно замены аргумента.
Непрерывность дифференцируемой функции
Если функция y = f (x) имеет производную в точке х = х0, то говорят, что при данном значении аргумента х = х0 функция дифференцируема.
Если функция дифференцируема в каждой точке интервала (a, b), то говорят, что она дифференцируема на этом интервале.
Если функция дифференцируема в некоторой точке х = х0, то она в этой точке непрерывна.
Доказательство. Пусть в точке х = х0 существует производная
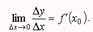 Так как разность между функцией и её пределом есть бесконечно малая величина, то из определения производной следует соотношение
Так как разность между функцией и её пределом есть бесконечно малая величина, то из определения производной следует соотношение
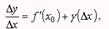
где γ (Δx) — является бесконечно малой величиной своего аргумента. Тогда Δy = f '(x0)·Δx + γ (Δx)·Δx и откуда следует, что Δy → 0 при Δx → 0, а это означает непрерывность функции у = f (x) в точке х0. Таким образом, в точках разрыва функция не может иметь производной. Однако и непрерывность функции не гарантирует существование производной в некоторой точке.
Теоремы Ролля, Лагранжа и Коши. Правило Лопиталя.
Теорема Ролля
Теорема 1.1. Если функция  непрерывна на отрезке
непрерывна на отрезке 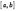 , дифференцируема во всех его внутренних точках, а на концах отрезка
, дифференцируема во всех его внутренних точках, а на концах отрезка 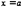 ,
, 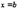 обращается в ноль, то существует, по крайней мере, одна точка
обращается в ноль, то существует, по крайней мере, одна точка 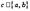 , в которой
, в которой 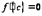 .
.
Следует отметить, что данная теорема справедлива и в том случае, когда на концах отрезка 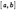 функция не обращается в ноль, но принимает равные значения
функция не обращается в ноль, но принимает равные значения 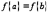 .
.
Геометрический смысл данной теоремы следующий: если непрерывная кривая пересекает ось 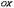 в двух точках
в двух точках 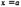 ,
, 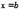 или принимает в них равные значения, то, по крайней мере, в одной точке между
или принимает в них равные значения, то, по крайней мере, в одной точке между 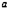 и
и 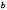 касательная к кривой параллельна оси
касательная к кривой параллельна оси 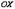 .
.
Необходимо отметить, что если не во всех точках 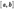 у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции (ри
у рассматриваемой функции существует производная, то теорема может не выполняться. Это касается, например, функции (ри 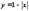 Данная функция непрерывна на отрезке
Данная функция непрерывна на отрезке 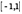 и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.
и обращается в ноль на его концах, но ни в одной точке внутри отрезка производная не равна нулю.
Теорема Лагранжа
Теорема. Если функция 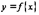 непрерывна на отрезке
непрерывна на отрезке 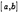 и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка
и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка 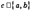 , в которой
, в которой 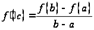 .
.
Согласно теореме Ролля в точке 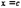 производная
производная 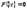 , то есть
, то есть 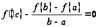 и
и 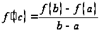 ,
,
что и требовалось доказать.
Геометрический смысл теоремы Лагранжа следующий: внутри отрезка 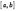 существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при
существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при 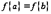 теорема переходит в теорему Ролля.
теорема переходит в теорему Ролля.
Теорема Коши
Теорема. Если функции 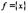 и
и 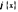 непрерывны на отрезке
непрерывны на отрезке 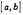 и дифференцируемы во всех его внутренних точках, причем
и дифференцируемы во всех его внутренних точках, причем 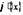 не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка
не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка 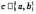 , в которой
, в которой 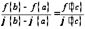 .
.
Данная функция непрерывна на отрезке 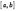 и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках
и дифференцируема во всех его внутренних точках. Кроме того, вычисление ее в точках 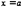 и
и 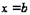 дает:
дает: 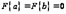 . Значит, функция
. Значит, функция 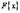 удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка
удовлетворяет требованиям теоремы Ролля, то есть существует хотя бы одна точка 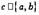 , в которой
, в которой 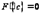 .
.
В случае, когда 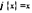 , теорема Коши переходит в формулировку теоремы Лагранжа.
, теорема Коши переходит в формулировку теоремы Лагранжа.
Правило Лопиталя
Теорема. Пусть функции 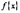 и
и 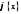 непрерывны и дифференцируемы во всех точках полуинтервала
непрерывны и дифференцируемы во всех точках полуинтервала 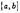 и при
и при  совместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при
совместно стремятся к нулю или бесконечности. Тогда, если отношение их производных имеет предел при 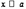 , то этот же предел имеет отношение и самих функций, то есть
, то этот же предел имеет отношение и самих функций, то есть 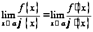 .
.
50ВОПРОСФормула Тейлора и различные формы её остаточного члена. Основные разложения элементарных функций по формуле Тейлора.
Теорема:
· Пусть функция 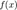 имеет имеет  производную в некоторой окрестности точки производную в некоторой окрестности точки 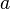 , , 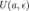 · Пусть · Пусть  · Пусть · Пусть 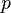 — произвольное положительное число, тогда: — произвольное положительное число, тогда:  точка точка 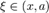 при при  или или 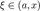 при при  : : 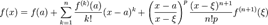 |
Это формула Тейлора с остаточным членом в общей форме (форма Шлёмильха — Роша).
[править]Различные формы остаточного члена
В форме Лагранжа:
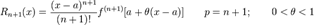
В форме Коши: 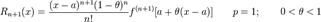
В интегральной форме: 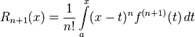
Разложение основных элементарных функций
- Положив x0=0 и вычислив соответствующие производные в нуле, получим формулы Тейлора для основных элементарных функций:
-
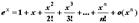 ;
; -
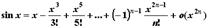 ;
; -
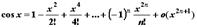 ;
; -
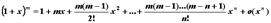 ;
; -
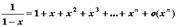 ;
; -
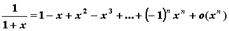 ;
; -
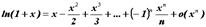
51 ВОПРОСЭкстремумы функции. Теорема Ферма. Необходимые и достаточные условия экстремума.
в точке x0 функция достигает экстремума, если для любых x из некоторой окрестности точки x0 выполняется неравенство f (x) ≤ f (x0) (минимум) илиf (x) ≥ f (x0) (максимум).
Теорема Ферма. Если функция f (x) дифференцируема в точке x0 и достигает в ней экстремума, то 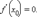 |
Необходимое условие экстремума. Во всех точках экстремума производная функции не существует или равна нулю.
Обратное, вообще говоря, неверно. Так, точка x = 0 функции y = x3 не является ни максимумом, ни минимумом.
Точки, в которых производная функции равна нулю, называются стационарными точками функции. Точки, в которых производная функции равна нулю или не существует, называются критическими точками. Таким образом, все экстремумы являются критическими точками
