Формула вычисления длины дуги кривой

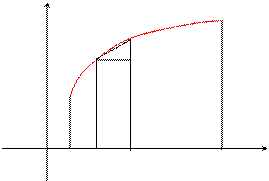
Пусть плоская кривая АВ задана уравнением y= f(x), где f(x) непрерывная на отрезке

[a, b] функция. Для нахождения длины кривой разобьем ее на n маленьких кусочков ∆L_i дуги. При большом числе разбиения дугу∆L_i можно спрямить кусочком прямой (хорды) близкой по размеру.

Dy_i y DL y = f(x)

_i

a Dx_i b x

Тогда кривую АВ можно заменить ломанной кривой, построенной из прямых кусочков ∆L_i.и вписанной в эту кривую.

Длина ломаной линии, которая соответствует дуге, может быть найдена как 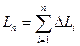. Тогда длина дуги равна L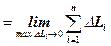

Из геометрических соображений: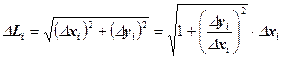

Тогда можно показать, что

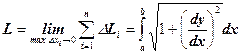
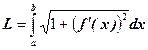(17)

Если уравнение плоской кривой задано параметрически, {x=φ(t), y=ψ(t), α≤t≤β} то с учетом правил вычисления производной параметрически заданной функции , получаем

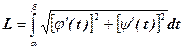, (18)

Если задана пространственная кривая, и {х = j(t), у = y(t) и z = Z(t)}, то

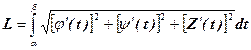(19)

Если кривая задана в полярных координатахr = f(j) , (α≤φ≤β) то

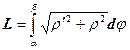, (20)

Для вывода формулы (20) надо вспомнить , как перевести уравнение кривой заданной в полярной системе координат в уравнение в параметрической форме и воспользоваться формулой (18).

Пример 16: Найти длину окружности, заданной уравнением x² + y² = a².

1 способ.Выразим из уравнения переменную у: 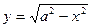- уравнение верхней половины окружности.

Найдем производную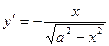

и по формуле (17) длину четверти окружности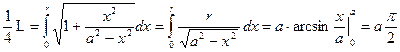

Тогда L = 2pa. Получили общеизвестную формулу длины окружности.

2 способ. Если представить заданное уравнение окружности в полярной системе координат:, x=ρcosφ, y=ρsinφ , то получим: ρ²cos²j + ρ²sin²j = a², т.е. функция

r = f(j) = a=const является уравнением окружности в полярной системе координат и производная этой функции 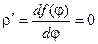тогда

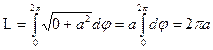
22. Кривые второго порядка. Определение. Свойства. Канонические уравнения. Уравнение в полярной системе координат.

Кривой второго порядка называется множество точек, координаты которых в некоторой (а значит и в любой) декартовой системе координат удовлетворяют уравнению второго порядка:

(1) a11x 2 + 2a12xy + a22y 2 + 2b1x + 2b2y + c = 0.

§ 1.2. Аналитическое определение и классификация 11 Если левая часть уравнения (1) разлагается на два множителя первой степени, то кривая является объединением двух прямых (возможно, совпадающих). В этом случае она называется вырожденной. Вырожденной считается также кривая, содержащая ровно одну действительную точку (например, x 2 + y 2 = 0). В курсе аналитической геометрии показывается (см., например, [1]), что для любой невырожденной кривой существует система координат, в которой ее уравнение имеет достаточно простой вид. Опишем основную идею этого упрощения. Вначале совершим поворот осей координат на угол f. Это значит, что в уравнении (1) координаты x и y надо заменить соответственно на x cos f − y sin f и x sin f + y cos f. Выбирая значение f, можно до- биться того, что коэффициент при произведении xy станет равен нулю. Затем перенесем начало координат в точку (x0, y0), т. е. заменим x на x + x0 и y на y + y0. Выбором значений (x0, y0) можно добиться того, что уравнение (1) примет один из следующих канонических видов (I), (II), (III). Непосредственное вычисление показывает, что кривая (I) x 2 a 2 + y 2 b 2 = 1, a > b > 0, является эллипсом с центром в начале координат, фокусами в точках (± √ a 2 − b 2, 0) и большой и малой полуосями (т. е. половинами длин соответствующих осей), равными соответственно a, b. В частном случае a = b эллипс (I) является окружностью. Кривая (II) x 2 a 2 − y 2 b 2 = 1, a > 0, b > 0, является гиперболой, пересекающей свою действительную ось в двух точках, расстояние между которыми равно 2a. Величина a называется действительной, а b –– мнимой полуосью гиперболы. Прямые x/y = = ±a/b являются асимптотами гиперболы, а точки (± √ a 2 + b 2, 0) –– ее фокусами. При a = b гипербола (II) будет равносторонней. В случае (III) y 2 = 2px, p > 0, кривая является параболой, ось которой совпадает с осью абсцисс, фокус находится в точке (p/2, 0), а уравнение директрисы x = −p/2. Кривая x 2 a2 + y 2 b 2 = −1 называется мнимым эллипсом и не содержит ни одной действительной точки.

Пример.

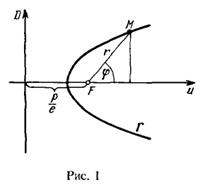Пусть Γ−Γ− эллипс, ветвь гиперболы или парабола, F−F− фокус этой кривой, D−D−соответствующая директриса. Вывести уравнение кривой ΓΓ в полярной системе координат, полюс которой совпадает с фокусом а полярная ось сонаправлена с осью кривой (см рисунок 1) .

Решение.

Общее свойство эллипса, гиперболы и параболы состоит в следующем

M∈Γ⇔ρ(M,F)/ρ(M,D)=const=e,

где e− эксцентриситет кривой ( e<1 для эллипса, e>1для гиперболы и e=1для параболы)

Обозначим расстояние от фокусы до директрисы через p/e(p− параметр кривой, называемый полуфокальным параметром). Тогда из рисунка 1 следует, что ρ(M,F)=r и ρ(M,F)=r и ρ(M,D)=p/e+rcosφ.

Подставляя эти выражения в (1), получаем

r/(p/e+rcosφ)=e,

откуда

r=p/(1−ecosφ).(2)

Уравнение (2) и есть искомое уравнение в полярной системе координат, общее для эллипса, гиперболы и параболы.

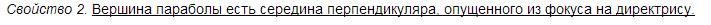
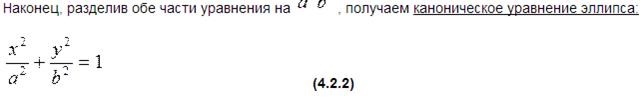
23. Расходящиеся прямые на плоскости Лобачевского.

Определение 17.1.Две прямые плоскости Лобачевского называются расходящимися, если они не пересекаются и не параллельны.

Очевидно, как следует из теоремы 13.1 (см. § 13), на плоскости Лобачевского существуют расходящиеся прямые. В качестве примера можно рассмотреть две прямые, имеющие общий перпендикуляр. Эти прямые не пересекаются и не параллельны (см. следствие теоремы 14.4, §14). Используя введенное определение, можно провести классификацию взаимного расположения прямых плоскости Лобачевского. Две прямые либо пересекаются, либо не имеют общих точек. Если они не пересекаются, то либо расходятся, либо параллельны. Докажем признак расходимости прямых.

Теорема 17.2 (Признак расходимости прямых на плоскости Лобачевского).Две прямые плоскости Лобачевского являются расходящимися тогда и только тогда, когда они имеют общий перпендикуляр.

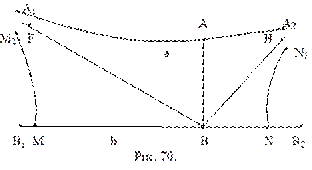Доказательство.Достаточностьэтого утверждения нами по сути доказана. Если у прямых имеется общий перпендикуляр, то они расходятся. Докажем необходимость. Пусть даны две расходящиеся прямые a и b. Для дальнейших рассуждений удобно их рассматривать как направленные прямые: 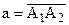и 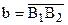. Выберем на прямой а произвольную точку А и опустим из нее перпендикуляр АВ на прямую b (рис. 70). Проведем через точку В направленные прямые 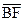и 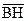, соответственно параллельные прямым 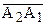и 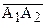. Угол АВВ₁, также, как уголАВВ₂ по построению прямые, поэтому углы FBB₁ и HBB₂ – острые. Следовательно, существуют отрезки, для которых эти углы служат углами параллельности. Отложим их от точки В, получим точки М и N. Для отрезка ВМ углом параллельности является угол FBB₁, а для отрезка BN – угол HBB₂. Восставим в точках М и N перпендикуляры 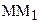и 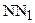к прямой b (см. рис. 70). Так как угол FBB₁ служит углом параллельности отрезка ВМ, то 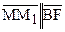. Но с другой стороны, 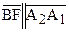. Из свойства транзитивности понятия параллельности направленных прямых по Лобачевскому следует, что 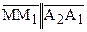. Аналогично доказывается, что перпендикуляр 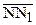параллелен направленной прямой 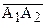. Таким образом, мы построили на одной из расходящихся прямых, прямой b, две точки M и N, перпендикуляры в которых к b параллельны второй прямой а.

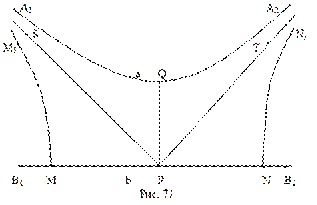Обозначим через Р середину отрезка MN. Опустим из точки Р перпендикуляр PQ на прямую а (рис. 71). Проведем через точку Р направленные прямые 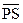и 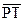, параллельные прямой а: 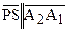, 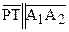. Но перпендикуляры, восставленные в точках М и N к прямой b также параллельны прямой а: 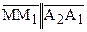, 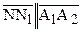. Поэтому, в силу свойства транзитивности параллельности прямых на плоскости Лобачевского 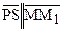, 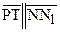(см. рис. 71). По построению, прямая PQ перпендикулярна прямой а, покажем, что она также перпендикулярна прямой b. Для этого достаточно доказать, что

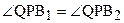. (1)

Так как 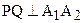, 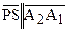и 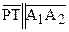, то углы QPS и QPT являются углами параллельности одного и того же отрезка PQ. Отсюда следует, что

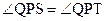. (2)

С другой стороны, 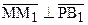, , 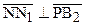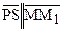и 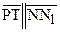. Отсюда следует, что углы SPM и TPN служат углами параллельности отрезков PM и PN. Так как эти отрезки равны друг другу по построению, то

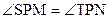. (3)

Так как 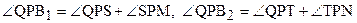, то отсюда и из равенств (2) и (3) следует соотношение (1). Теорема доказана.

25. Кольцо. Теорема о делении с остатком. Алгоритм Евклида.

Пусть на множестве S заданы две алгебраические операции: сложение + и умножение ·. Структура R = (S; +, ·) называется кольцом, если 1) множество S с операцией сложения + является абелевой группой, т.е. а) операция сложения + коммутативна и ассоциативна; б) существует нулевой (нейтральный) элемент 0 относительно операции сложения +; в) для каждого элемента a ∈ S найдется противоположный (симметричный) элемент −a ∈ S относительно операции сложения +; 2) выполнены свойства дистрибутивности, т.е. для любых элементов a, b, c ∈ S верно a · (b + c) = a · b + a · c; (a + b) · c = a · c + b · c. Виды колец Пусть R = (S; +, ·) – кольцо. Кольцо R называется - коммутативным (ассоциативным) кольцом, если операция умножения · коммутативна (ассоциативна); - кольцом с единицей, если в нем есть единичный элемент 1 ∈ S (т.е. нейтральный элемент по умножению ·); - кольцом без делителей нуля, если для любых элементов a, b ∈ S равенство a · b = 0 влечет, что или a = 0, или b = 0; - целостным кольцом, если оно коммутативно, ассоциативно, с единицей и без делителей нуля; - полем, если в нем S 6= {0}, и множество S \ {0} с операцией умножения · образует абелеву (мультипликативную) группу

Теорема.

Любое целое число a возможно представить единственным образом через целое и отличное от нуля число b в виде a=b·q+r, где q и r – некоторые целые числа, причем .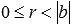

Доказательство.

Сначала докажем возможность представления a=b·q+r.

Если целые числа a и b такие, что a делится на b нацело, то по определению существует такое целое число q, что a=b·q. В этом случае имеет место равенство a=b·q+r при r=0.

Теперь будем считать, что b – целое положительное число. Выберем целое число q таким образом, чтобы произведение b·q не превышало числа a, а произведение b·(q+1) было уже больше, чем a. То есть, возьмем q таким, чтобы выполнялись неравенства b·q<a<b·(q+1). После вычитания из всех частей этого неравенства произведения b·q приходим к неравенствам вида0<a−b·q<b. Так как значение выражения a−b·q положительно и не превышаетb (b – положительное число), то это значение можно принять в качестве r, то есть, r=a−b·q. Откуда получаем нужное представление числа a вида a=b·q+r.

Осталось доказать возможность представления a=b·q+r для отрицательных b.

Так как модуль числа b в этом случае является положительным числом, то для 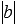имеет место представление 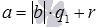, где q₁ – некоторое целое число, а r– целое число, удовлетворяющее условиям 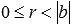. Тогда, приняв q=−q₁, получаем нужное нам представление a=b·q+r для отрицательных b.

Переходим к доказательству единственности.

Предположим, что помимо представления a=b·q+r, q и r – целые числа и 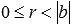, существует еще одно представление a=b·q₁+r₁, где q₁ и r₁ – некоторые целые числа, причем q₁≠q и .

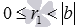После вычитания из левой и правой части первого равенства соответственно левой и правой части второго равенства, получаем 0=b·(q−q₁)+r−r₁, которое равносильно равенству r−r₁=b·(q₁−q). Тогда должно быть справедливо и равенство вида 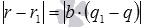, а в силу свойств модуля числа - и равенство .

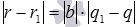Из услови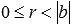й и 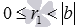можно сделать вывод, что 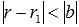. Так как qи q₁ – целые и q≠q₁, то 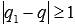, откуда заключаем, что 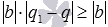. Из полученных неравенств 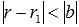и 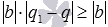следует, что равенство вида 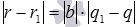невозможно при нашем предположении. Поэтому, не существует другого представления числа a, кроме a=b·q+r.

Алгоритм Евклида – это алгоритм нахождения наибольшего общего делителя (НОД) пары целых чисел.
Наибольший общий делитель (НОД) – это число, которое делит без остатка два числа и делится само без остатка на любой другой делитель данных двух чисел. Проще говоря, это самое большое число, на которое можно без остатка разделить два числа, для которых ищется НОД.