Арифметические приложения теории сравнений
С помощью теории сравнений можно решать различные математические задачи. Рассмотрим основные арифметические приложения теории сравнений – нахождение длины периода десятичной дроби и признаки делимости.
Теорема 5.20. Пусть  обыкновенная правильная дробь, где
обыкновенная правильная дробь, где  некоторое целое число,
некоторое целое число,  натуральное число, взаимнопростое с числом
натуральное число, взаимнопростое с числом  и с числом 10. Разложение дроби
и с числом 10. Разложение дроби  в бесконечную десятичную дробь будет содержать
в бесконечную десятичную дробь будет содержать  цифр в периоде.
цифр в периоде.
Замечание. Требование взаимной простоты числа  с числом 10, очевидно, означает, что число
с числом 10, очевидно, означает, что число  не делится ни на 2, ни на 5.
не делится ни на 2, ни на 5.
Пример. Найдём число цифр в периоде при разложении обыкновенной дроби  в бесконечную десятичную дробь.
в бесконечную десятичную дробь.
Очевидно, что числа 7 и 13 – взаимнопростые, поэтому, в соответствии с теоремой 5.20, для решения задачи необходимо вычислить показатель  Делителями функции Эйлера
Делителями функции Эйлера  являются числа: 1, 2, 3, 4, 6, 12. Непосредственной проверкой убеждаемся в справедливости сравнения
являются числа: 1, 2, 3, 4, 6, 12. Непосредственной проверкой убеждаемся в справедливости сравнения

Следовательно, разложение дроби  в бесконечную лесятичную дробь содержит
в бесконечную лесятичную дробь содержит  цифр.
цифр.
Теорема 5.21 (общий признак делимости). Пусть дана систематическая запись числа  в
в  й системе счисления (
й системе счисления (  натуральное число):
натуральное число):

где

 натуральное число, а числа
натуральное число, а числа  таковы, что
таковы, что

Тогда справедливо сравнение

Замечание. Из теоремы 5.21 и определения 5.1 следует справедливость утверждения:

Для применения общего признака делимости в системе счисления с основанием  нужно знать остатки от деления на заданное
нужно знать остатки от деления на заданное  степеней числа
степеней числа  т. е. числа
т. е. числа  Умножая эти числа на соответствующие цифры числа
Умножая эти числа на соответствующие цифры числа  а затем суммируя полученные произведения, можно узнать, делится ли число
а затем суммируя полученные произведения, можно узнать, делится ли число  на число
на число  или не делится. Указанным способом получают частные признаки делимости.
или не делится. Указанным способом получают частные признаки делимости.
Пример. Выведем признак делимости на 3 в десятичной системе счисления. Систематическая запись числа  в десятичной системе счисления имеет вид:
в десятичной системе счисления имеет вид:

По теореме 5.21, имеет место сравнение

Найдём числа  Имеем сравнения:
Имеем сравнения:

Таким образом, остатки степеней числа 10 при делении на 3 равны 1, тогда получим сравнение:

т. е. число  в десятичной системе счисления делится на 3 тогда и только тогда, когда сумма цифр этого числа делится на 3.
в десятичной системе счисления делится на 3 тогда и только тогда, когда сумма цифр этого числа делится на 3.
30. Векторное пространство над полем. Базис и размерность векторного пространства. Переход от одного базиса к другому.






31.Простые числа. Бесконечность множества простых чисел. Каноническое разложение составного числа.
Определение: Всякое натуральное число p>1, не имеющее других натуральных делителей, кроме 1 и p, называется простым числом. Наименьшее простое число – 2. 1 – не простое и не составное, так как имеет один делитель 1. 1) Если p>1 является наименьшим делителем целого числа n>1, то оно простое (число p). 2) Если произведение , где p – простое число, то, по крайней мере, либо , либо . 3) Натуральное число a и p – простое число, либо взаимно простые, либо . Теорема. Множество простых чисел бесконечно. Доказательство (Евклид). Предположим, что множество простых чисел конечно. Пронумеруем их в порядке возрастания: p1, p2, …, pn. Рассмотрим . Докажем, что Q – простое. По предположению число Q не может быть простым, так как . Тогда Q – составное число и должно делиться на простое число pm, но тогда , что невозможно. Следовательно, число Q – простое. Мы получили ещё одно простое число, что противоречит нашему предположению. Следовательно, множество простых чисел – бесконечно. Что и требовалось доказать.
Составным числом называется натуральное число, которое имеет более двух делителей.
Любое составное число может быть разложено в произведение простых множителей, причём единственным способом (с точностью до порядка множителей).
Объединяя в разложении числа 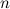 одинаковые простые сомножители, получаем так называемое каноническое разложение числа
одинаковые простые сомножители, получаем так называемое каноническое разложение числа 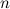 :
:

где  , - различные простые числа, а
, - различные простые числа, а  - натуральные.
- натуральные.
Задание. Найти каноническое разложение составных чисел 108 и 280.
Решение. Для нахождения простых множителей будем последовательно делить заданные числа на простые в порядке их возрастания.

Например запишем число 108 и проведем вертикальную линию. Далее возьмем наименьшее простое число 2. Разделим его на него 108, получается 54. Два записываем справа от вертикальной черты, а результат деления 54 под числом 108. Далее можно еще раз поделить на 2, получим 27. Число 27 уже не делится на 2, берем следующее простое число: 3, делим на него, получим 9, затем еще раз на 3, получаем 3, разделив его еще раз на три, получаем 1. Все мы нашли все делители числа 108.
Выпишем множители из правой части: 
Заменим одинаковые множители степенями:  . Получили каноническое разложение этого числа.
. Получили каноническое разложение этого числа.
Разложим таким же образом число 280. Получим следующее разложение:  . Тогда, каноническое разложение этого числа имеет вид:
. Тогда, каноническое разложение этого числа имеет вид:  .
.
Ответ. 

32. Корни многочлена. Схема Горнера. Теорема Виета.

Схема Горнера – способ деления многочлена
Pn(x)=∑i=0naixn−i=a0xn+a1xn−1+a2xn−2+…+an−1x+an
на бином x−a. Работать придётся с таблицей, первая строка которой содержит коэффициенты заданного многочлена. Первым элементом второй строки будет число a, взятое из бинома x−a:

После деления многочлена n-ой степени на бином x−a, получим многочлен, степень которого на единицу меньше исходного, т.е. равна n−1.
Пример №2
Разделить многочлен x4+3x3+4x2−5x−47 на x+3 по схеме Горнера.
Решение
Сразу оговорим, что выражение x+3 нужно представить в форме x−(−3). В схеме Горнера будет учавствовать именно −3. Так как степень исходного многочлена x4+3x3+4x2−5x−47 равна четырём, то в результате деления получим многочлен третьей степени:

Полученный результат означает, что
x4+3x3+4x2−5x−47=(x+3)(x3+0⋅x2+4x−17)+4=(x+3)(x3+4x−17)+4
В этой ситуации остаток от деления x4+3x3+4x2−5x−47 на x+3 равна 4. Или, что то самое, значение многочлена x4+3x3+4x2−5x−47 при x=−3 равно 4. Кстати, это несложно перепроверить непосредственной подстановкой x=−3 в заданный многочлен:
x4+3x3+4x2−5x−47=(−3)4+3⋅(−3)3−5⋅(−3)−47=4.
