ПрактикалыҚ сабаҚ 15. остроградский-гаусс жӘне стокс формулары.

Пример. Бірінші типті беттік интегралды есептеу 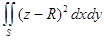по верхней стороне полусферы

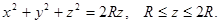
Преобразуем уравнение поверхности к виду: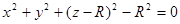

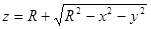Заданная поверхность проецируется на плоскость XOY в круг, уравнение которого: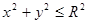

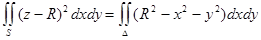
Для вычисления двойного интеграла перейдем к полярным координатам:

,

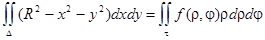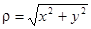
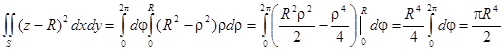
Әдебиеттер

Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

Бақылау сұрақтар

1. Бірінші типті беттік интегралдың анықтамасы?
2. Айқындалған теңдеумен берілген беттің ауданы?
3. Жалпы жағдайдағы беттің ауданы?
4. Екінші типті беттік интегралдың анықтамасы?
5. Жай қос интегралға келтіру?

СТУДЕНТТІҢ ӨЗДІК ЖҰМЫСЫ

СТУДЕНТТЕРДІҢ ӨЗДІК ЖҰМЫСТАРЫНА АРНАЛҒАН ТАҚЫРЫПТАРДЫҢ ТІЗІМІ

5.1 Цилиндрлік кесектің көлемі тұралы есеп.

5.2 Екі еселі интегралды қайталанған интегралға келтіру

5.3 Қисық сызықты облыс жағдайында қос интегралды қайталанған интегралға келтіру

5.4 Екі еселі интегралдарда айнымалыларды ауыстыру

5.5 Екі еселі интегралды геометриялық қолданулары

5.6 Екі еселі интегралды механикалық қолданулары

5.7 Дененің массасын есептеу тұралы есеп.

5.8 Үш еселі интегралды есептеу.

5.9 Үш еселі интегралдарды қолданулары

5.10 Бірінші және екінші типті қисықсызықты интегралдарды есептеу. Грин формуласы.

5.11 Бірінші және екінші типтік беттік интегралдары

5.12 Остроградский-Гаусс және Стокс формулары.

Бақылау есептер

Задача 1.Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 155-166с. №1.6-50.6

Задача 2.Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 166-172с. №51.6-76.6

Задача 3. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 173-176с. №77.6-93.6

Задача 4.Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 176-182с. №94.6-121.6

Задача 5.Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 182-185с. №122.6-145.6

Задача 6. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 185-190с. №146.6-172.6

Задача 7. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 190-192с. №173.6-185.6

Задача 8. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 192-194с. №186.6-196.6

Задача 9. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 194-198с. №197.6-228.6

Задача 10. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971, 198-207с. №229.6-273.6

Тестік сұрақтар

$$$ 1

Есепте ,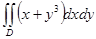

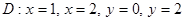
A)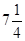

B) 7

C) 8

D) 8,5

E)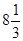

$$$ 2

Есепте ,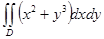

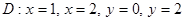
A)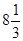

B) 7

C)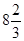

D) 8

E) 8.5

$$$ 3

Есепте ,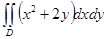

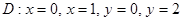
A)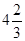

B)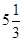

C)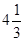

D) 4

E)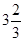

$$$ 4

Есепте ,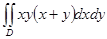

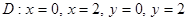
A) 10

B) 11

C)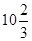

D)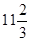

E) 12

$$$ 5

Есепте ,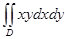

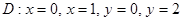
А) 4

B) 3

C) 0

D) 1

E) 2

$$$ 6

Есепте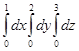

A) -2

B) 0

C) 2

D) 4

E) 6

$$$ 7

Есепте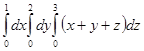

A) 9

B) 27

C) 24

D) 18

E) 36

$$$ 8 B

Есепте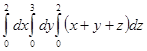

A) 36

B) 38

C) 40

D) 42

E) 44

$$$ 9

Есепте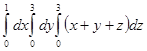

A) 29,5

B) 31,5

C) 30,5

D) 32,5

E) 33,5

$$$ 10

Есепте ,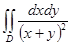

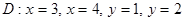
A)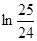

B)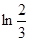

C)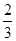

D)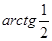

E)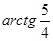

$$$ 11

Есепте ,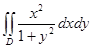

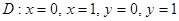
A)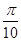

B)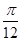

C)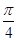

D)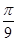

E)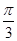

$$$ 12

Есепте ,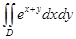

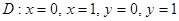
A) е

B)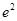

C)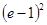

D)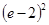

E)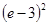

$$$ 13

у=0, у=1, у=х³ сызықтарымен шектелген фигураның ауданын тап

A) 1

B)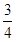

C)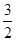

D)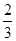

E)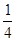

$$$ 14

х=0, х=2, у=0, у=е^х сызықтарымен шектелген фигураның ауданын тап

A)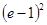

B)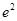

C)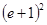

D)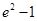

E)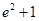

$$$ 15

: х=0, у=1, у=3, 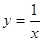сызықтарымен шектелген фигураның ауданын тап

A) ln4

B) 1

C) ln3

D) ln5

E) ln6

$$$ 16

х=y, х=1, 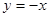сызықтарымен шектелген фигураның ауданын тап

A) 0,5

B) 3

C) 2

D)1,5

E) 1

$$$ 17

Есепте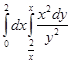

A) 1

B) 0

C) 2,5

D)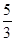

E)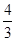

$$$ 18

Есепте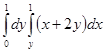

A)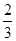

B)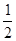

C)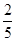

D)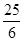

E)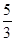

$$$ 19

Есепте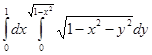

A)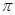

B)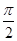

C)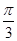

D)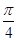

E)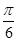

$$$ 20

Есепте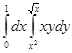

A)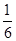

B)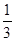

C) 0,25

D)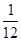

E) 0,5

$$$ 21

Есепте ,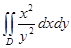

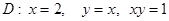
A)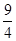

B) 2

C)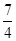

D) 3

E)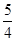

$$$ 22

Есепте ,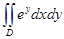

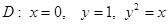
A) е-1

B) е+2

C) е

D) е-2

E)е+1

$$$ 23 C

Есепте ,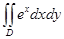

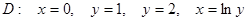
A) 1

B) 1,5

C) 0,5

D) 2

E)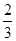

$$$ 24

Есепте ,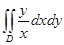

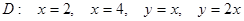
A) 7

B) 8

C) 10

D) 9

E) 6

$$$ 25 B

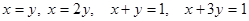сызықтарымен шектелген фигураның ауданын тап

A)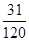

B)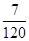

C)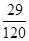

D)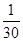

E)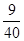

$$$ 26

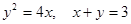сызықтарымен шектелген фигураның ауданын тап

A)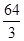

B) 3,5

C)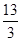

D)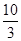

E) 4

$$$ 27

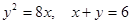сызықтарымен шектелген фигураның ауданын тап

A) 13

B)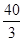

C)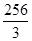

D)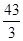

E)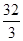

$$$ 28

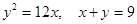сызықтарымен шектелген фигураның ауданын тап

A) 30

B) 192

C) 28

D) 32

E) 35

$$$ 29

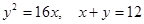сызықтарымен шектелген фигураның ауданын тап

A) 52

B)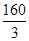

C)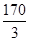

D) 60

E)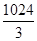

$$$ 30

Полярлық координаталарға көше отырып есепте ,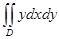

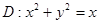
A) 0

B)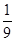

C)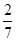

D)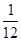

E)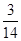

$$$ 31

Полярлық координаталарға көше отырып есепте ,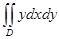

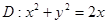
A)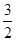

B) 0

C)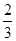

D)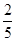

E)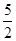

$$$ 32

Полярлық координаталарға көше отырып есепте ,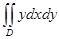

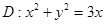
A) 2

B) 0

C)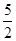

D)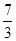

E)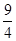

$$$ 33

Полярлық координаталарға көше отырып есепте ,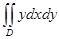

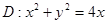
A) 0

B) 5

C) 4,5

D)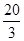

E)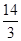

$$$ 34

Полярлық координаталарға көше отырып есепте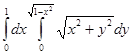

A)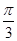

B)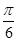

C)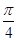

D)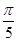

E)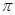

$$$ 35

Полярлық координаталарға көше отырып есепте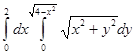

A)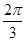

B)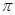

C)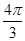

D)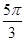

E) 25

$$$ 36

Есепте 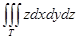, егер Т : 0≤х≤ 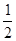, х≤у≤2х, 0≤z≤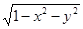

A)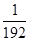

B)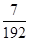

C) 8

D) 8,5

E)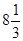

$$$ 37

Есепте 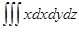,егер Т-х=0, у=0, z=0, х+у+z-1=0

A)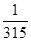

B) 7

C)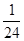

D) 8

E)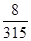

$$$ 38

Есепте 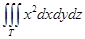, егерТ – сфера x²+y²+z²=R²

A)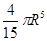

B)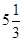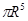

C)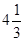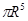

D) 4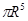

E)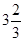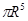

$$$ 39

Есепте 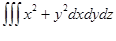, егер Т – z =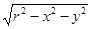

A)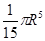

B)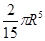

C)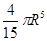

D)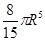

E)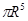

$$$ 40

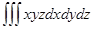, егер Т – х=0, х=1, у=2, у=5, z=2, z=4

A) 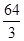B) 3 C) 0 D) 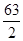E) 2 ln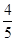

$$$ 41

Есепте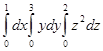

A) -12

B) 20

C) 12

D) 14

E) 16

$$$ 42

Есепте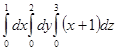

A) 9

B) 27

C) 12

D) 18

E) 36

$$$ 43

Есепте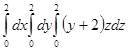

А) 36

B) 38

C) 40

D) 24

E) 44

$$$ 44

Есепте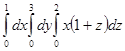

A) 14

B) 13

C) 18

D) 0

E) 15

$$$ 45

Есепте 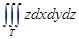, егер Т- призма x=y=z=0, z=3, x+y=2

A) 9

B) 2

C) 3

D) 8

E) 18

$$$ 46

Есепте 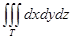, егер Т- параллелепипед x+y=1,х=0, y=0, z=0, z=3

А)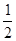

В)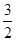

С) 2

D) 3

E)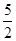

$$$ 47

Есепте 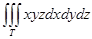, егер Т – х=у=z=0, x=1, y=2, z=3

A) 10

B) 11

C)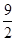

D)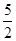

E) 20

$$$ 48

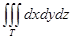, егер Т – x=y=z=0, x=2, y=4, z=5

A) 10

B) 40

C) 44

D) 55

E) 22

$$$ 49

Есепте 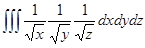, егер x=y=z=0, x=1, y=4, z=16

A) 25

B) 36

C) 64

D) 60

E) 29

$$$ 50

Есепте 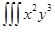dxdydz, егер Т – x=y=z=1, x=y=z=2

A) 1

B) 0

C)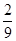

D)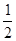

E)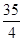

8 ӘДЕБИЕТТЕР

Негізгі әдебиеттер

8.1.1. Х.И.Ибрашев, Ш.Т.Еркеғұлов. Математикалық анализ курсы. 1-2 том. А., «Қазақтың мемлекеттік оқу-педагогика баспасы», -1963.

8.1.2. Фихтенгольц Г. М. Математикалық анализ негіздері, 2 Том.

8.1.3. Демидович Б. П.Задачи и упражнения по математическому анализу, 1978, Наука

8.1.4. Кузнецов Л. А. Сборник заданий по высшей математике, М. «Высшая школа», 1984.

8.1.5. Қадықайырұлы Қ. Дифференциалдық және интегралдық есептеулер, 1972, Мектеп

8.1.6. Г.Н.Берман. Сборник задач по курсу математического анализа. М., «Наука» - 1977.

8.1.7. Н.Я.Виленкин. Задачник по курсу математического анализа. ч. II., М.,«Просвещение» - 1971

8.1.8. Н.Темірғалиев. Математикалық анализ. А., «Мектеп», 1987.

8.1.9. В.И.Ильин, Э.Г.Позняк. Основы математического анализа. М., «Наука» - 1980, ч.1 и 2.

Қосымша әдебиеттер

8.2.1. Данко Л. Е., Попов Т. Я. Высшая математика в упражнениях и задачах. Часть 2., М.,

8.2.2. Запорожец А. Т. Задачи по математическому анализу.

8.2.3. С. М. Никольский Курс математического анализа. Том 1. М. «Высшая школа»,

1978.

8.2.4. Уваренков И. М. Маллер М.З. Курс математического анализа 1966, 2том Просвещение

8.2.5. Л.Д.Кудрявцев. Математический анализ, т.1 и 2. М., - 1970.

8.2.6. В.Ф.Бутузов. Математический анализ в вопросах и задачах. М., «Высшая школа» - 1988.