Практичне заняття 19. статистичні гіпотези

1. Порівняння двох середніх нормальних генеральних сукупностей, дисперсії яких відомі.

2. Порівняння двох дисперсій нормальних генеральних сукупностей.

Приклад. За заданими статистичними розподілами двох вибірок, реалізованих із двох генеральних сукупностей, ознаки яких мають нормальний закон розподілу зі значенням дисперсій генеральних сукупностей ,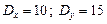

xi	12,2	13,2	14,2	15,2	16,2		yj	8,4	12,4	16,4	20,4	24,4

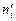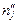при рівні значущості a = 0,01 перевірити правдивість нульової гіпотези 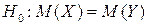, якщо альтернативна гіпотеза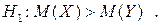

Розв’язання. Оскільки 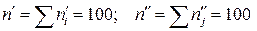, обчислимо , :

.

.

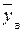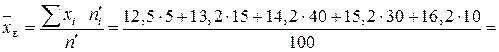
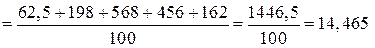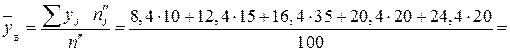
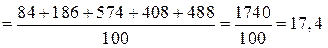Для альтернативної гіпотези 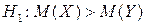будується правобічна критична область. Критичну точку 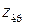знаходимо з рівності

.

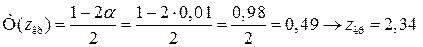Правобічна критична область зображена на рис. 131.

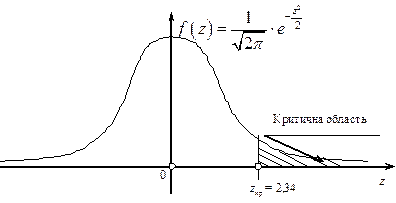
Рис. 131

Обчислимо спостережуване значення критерію

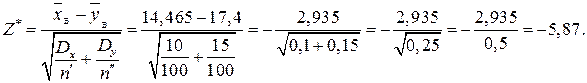
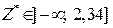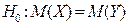Висновок. Оскільки , то не відхиляється.

Приклад. Ознаки Х і Y двох генеральних сукупностей, елементами яких є однотипні заклепки, мають нормальний закон розподілу зі значеннями дисперсій D_x = 2,2 мм², D_y = 2,8 мм².

При реалізації двох вибірок із генеральних сукупностей дістали статистичні розподіли:

yi	9,7	9,8	9,9		10,1	10,2		xj	8,9	9,2	9,5	9,8	10,1

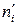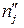При рівні значущості a = 0,001 перевірити правильність нульової гіпотези 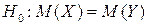, якщо альтернативна гіпотеза .

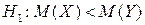Розв’язання. Ураховуючи, що 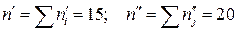, обчислимо

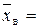
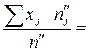
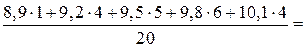
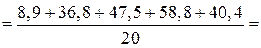
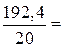
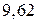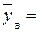
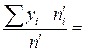
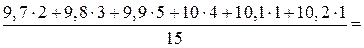
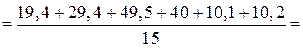
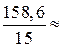
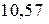мм.

мм.

При альтернативній гіпотезі 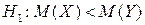будуємо лівобічну критичну область, критичну точку для якої знаходимо з рівності

.

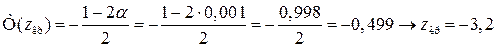Лівобічна критична область зображена на рис. 132.

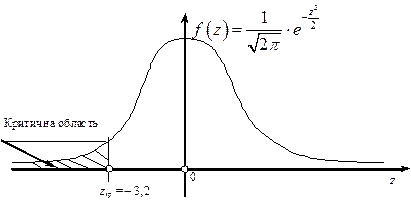
Рис. 132

Обчислюємо спостережуване значення критерію

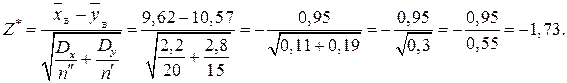
Висновок. Оскільки 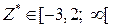, то відсутні підстави для відхилення .

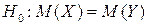Приклад. Для дослідження розтягування певного типу гуми після хімічного оброблення було відібрано шість її мотків, кожний з яких було розділено навпіл і одна його половина була піддана хімічній обробці, а друга – ні.

Потім за допомогою приладу, що вимірює розтягування матеріалу, мотки гуми були виміряні і результати вимірювання наведені у вигляді двох статистичних розподілів ознак Х і Y, які мають нормальний закон розподілу з відомими значеннями генеральних дисперсій D_x = 10; D_y = 16.

yi	16,7	17,2	17,3	18,1	18,4	19,1		xj	16,2	16,3		17,6	18,4

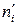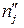При рівні значущості a = 0,001 перевірити правдивість нульової гіпотези 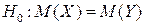, якщо альтернативна гіпотеза .

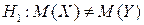Розв’язання. Обчислимо значення , .

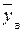Оскільки 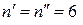, то маємо:

.

.

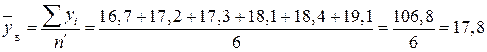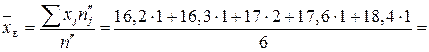
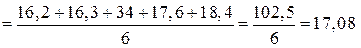При альтернативній гіпотезі 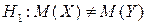будується двобічна критична область.

Оскільки 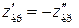, то 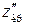обчислюємо, використовуючи рівність

.

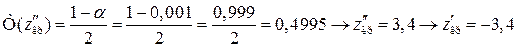Критична область зображена на рис. 133.

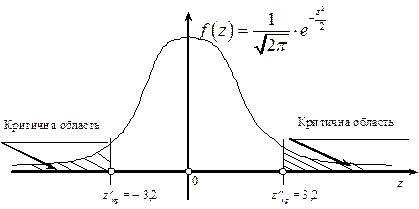
Рис. 133

Обчислимо спостережуване значення критерію

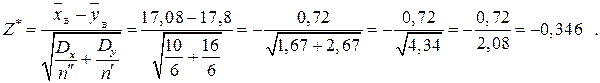
Висновок. Оскільки 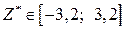, то немає підстав відхиляти .

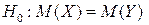Приклад. З допомогою двох радіовимірних приладів вимірювалась відстань до певного об’єкта. Результати вимірювання наведені у вигляді двох статистичних розподілів ознак: Y – відстань, виміряна першим радіоприладом, та Х – другим. При цьому Y і Х є незалежними між собою і підпорядковані нормальному закону розподілу. Статистичні розподіли мають такий вигляд:

yi, км

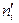xj, км

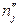При рівні значущості a = 0,01 перевірити правильність нульової гіпотези 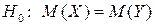, якщо альтернативна гіпотеза .

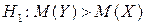Розв’язання. Значення дисперсій генеральних сукупностей невідомі. Необхідно обчислити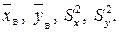

Оскільки 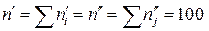, то

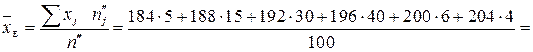
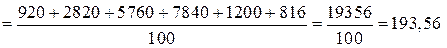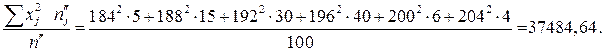
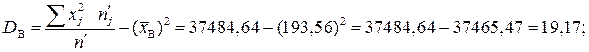
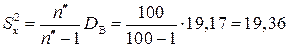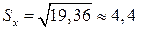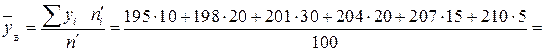
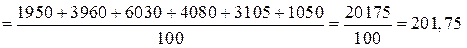км.

; .

км.

;

;

; .

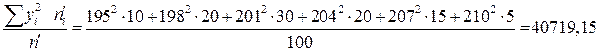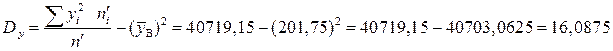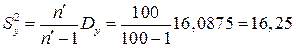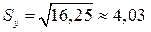При альтернативній гіпотезі 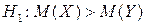будуємо правобічну критичну область, критична точка якої, ураховуючи те, що обсяг вибірки великий, знаходиться з рівності

.

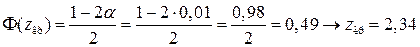Критична область зображена на рис. 134.

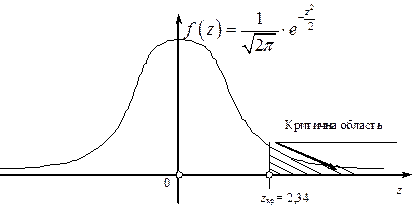
Рис. 134

Спостережуване значення критерію обчислюється так:

.

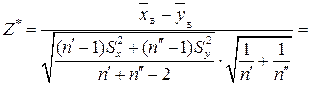
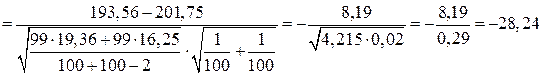Висновок. Оскільки 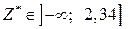, то відсутні підстави для відхилення .

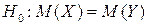Приклад. Протягом доби двома приладами вимірювали напругу в електромережі. Результати вимірювання наведено у вигляді статистичних розподілів

yi

xj

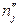Припускаючи, що випадкові величини Х і Y (напруга у вольтах) є незалежними і мають нормальний закон розподілу ймовірностей, за рівня значущості a = 0,001 перевірити правильність нульової гіпотези 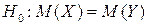при альтернативних гіпотезах:

1) ;

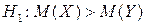2) .

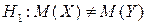Розв’язання. Обсяги вибірок відповідно дорівнюють , .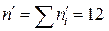

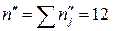Обчислимо значення , , , :

;

;

;

;

;

;

;

.

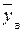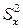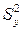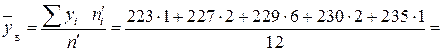
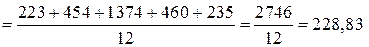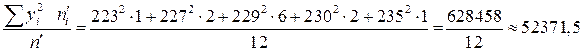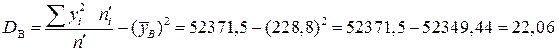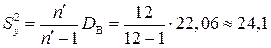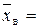
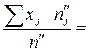
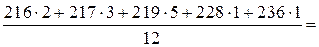
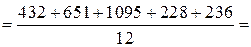
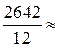
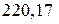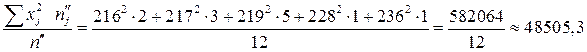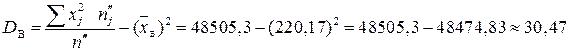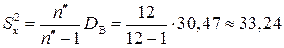1) Для перевірки правильності нульової гіпотези 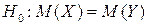при альтернативній гіпотезі 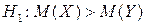будуємо правобічну критичну область. Ураховуючи, що статистичний критерій має розподіл Стьюдента з 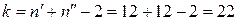та рівнем значущості a = 0,001, за таблицею (додаток 6) знаходимо критичну точку .

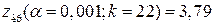Правобічна критична область зображена на рис. 135.

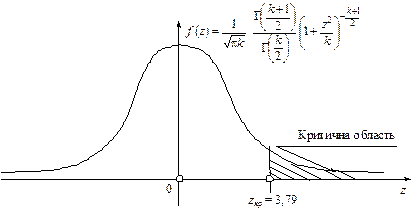
Рис. 135

За формулою (459) обчислюємо спостережуване значення критерію

.

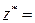
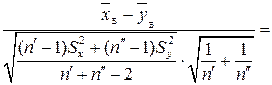
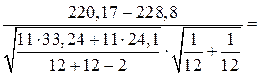
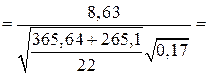
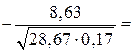
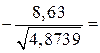
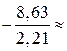
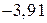Висновок. Оскільки 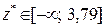, то 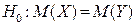приймається.

2) Для альтернативної гіпотези 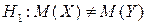будується двобічна критична область. Беручи до уваги, що 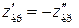, а 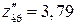, тоді 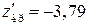. Двобічна критична область зображена на рис. 136.

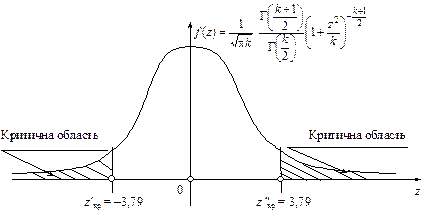
Рис. 136

З попередніх обчислень маємо .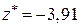

Висновок. Оскільки 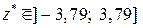, то в цьому разі немає підстав для прийняття .

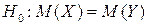Приклад. З двох вибірок обсягом 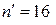, , 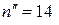реалізованих із двох генеральних сукупностей, ознаки яких Х і Y є незалежними і мають нормальний закон розподілу, oбчислені значення .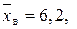

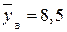
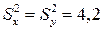При рівні значущості a = 0,001 перевірити правильність нульової гіпотези 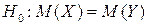, якщо альтернативна гіпотеза .

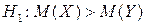Розв’язання. Статистичний критерій у цьому разі є випадковою величиною

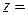
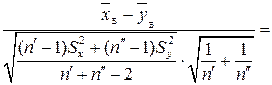
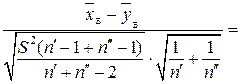
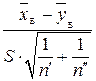, тобто 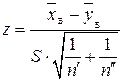, що має розподіл Стьюдента з 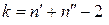ступенями свободи.

Для альтернативної гіпотези 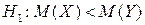будуємо лівобічну критичну точку. 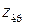знаходимо за таблицею (додаток 6). Звідси маємо, що .

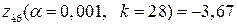Критична область зображена на рис. 137.

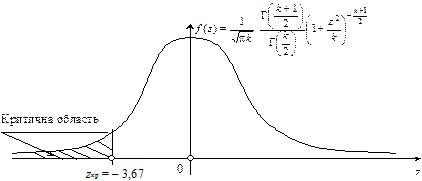
Рис. 137

Обчислимо спостережуване значення критерію

.

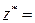
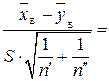
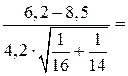
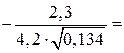
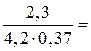
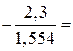
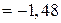Висновок. Оскільки 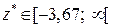, то 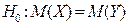приймається.

Приклад. Під час дослідження стабільності температури в термостаті дістали такі результати: 21,2; 21,8; 21,3; 21,0; 21,4; 21,3.

З метою стабілізації температури було використано удосконалений пристрій, після цього заміри температури показали такі результати: 37,7; 37,6; 37,6; 37,4. Чи можна за рівня значущості a = 0,01 вважати використання удосконаленого пристрою до стабілізатора температури ефективним?

Розв’язання. Очевидно, що ефективність стабілізаторів без удосконаленого пристрою і з ним залежить від дисперсій вимірюваних ними температур. Отже, задача звелась до порівняння двох дисперсій.

Обчислимо виправлені вибіркові дисперсії

;

;

;

;

;

;

;

.

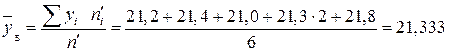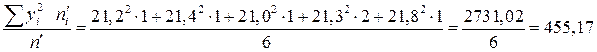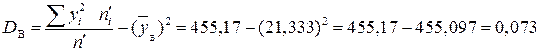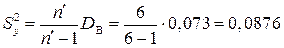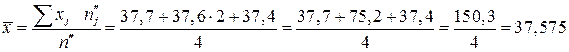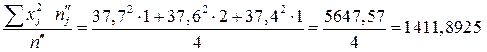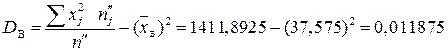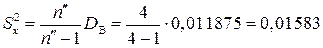Обчислимо спостережуване значення критерію

.

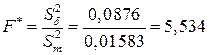Число ступенів вільності для більшої виправленої дисперсії 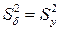, , 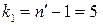для меншої , .

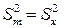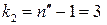Оскільки удосконалення стабілізатора температур може тільки зменшити дисперсію, то будуємо правобічну критичну область. Отже, .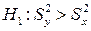

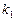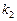Критичну точку знаходимо за таблицею (додаток 7) відповідно до заданого рівня значущості a = 0,01 і числа ступенів свободи = 5, = 3, .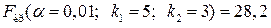

Схематично правобічна критична область зображена на рис. 138.

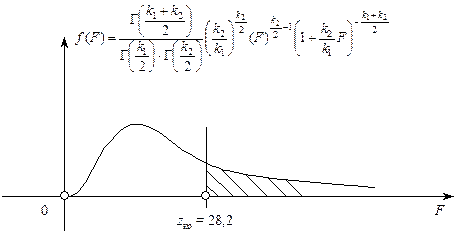
Рис. 138

Висновок. Оскільки 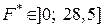, дані спостережень не дають підстав відхилити нульову гіпотезу, тобто вдосконалення термостабілізатора є ефективним.

Приклад. За заданими статистичними розподілами вибірок, які реалізовано з генеральних сукупностей, ознаки яких Х і Y є незалежними і мають нормальний закон розподілу,

yi	1,2	2,2	3,2	4,2	5,2

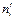xj	0,8	1,6	2,4	3,2

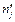при рівні значущості a = 0,01 перевірити правильність нульової гіпотези 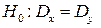, якщо альтернативна гіпотеза .

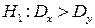Розв’язання. Обчислимо значення , :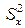

;

;

;

;

;

.

;

.

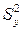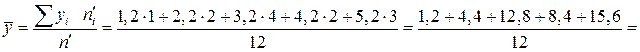
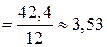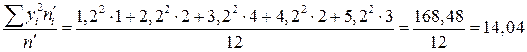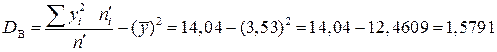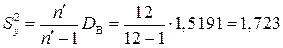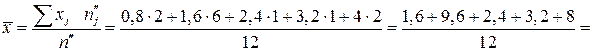
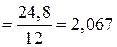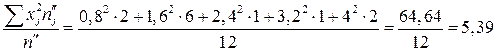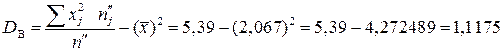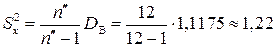Обчислимо спостережуване значення критерію .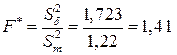

Для альтернативної гіпотези 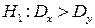будуємо правобічну критичну область. Знайдемо за таблицею (додаток 7) критичну точку

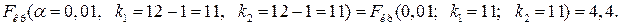
Критична область зображена на рис. 139.

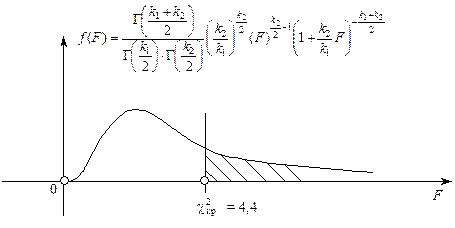
Рис. 139

Висновок. Оскільки 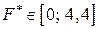, нульова гіпотеза 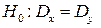є правильною.