Р е ш е н и е н е л и н е й н ы х у р а в н е н и й м е т о д о м
П о л о в и н н о г о д е л е н и я .
Пусть дано уравнение f (x)= 0 , ( 1 ) ,
один из корней которого отделен , т.е. найден отрезок ( а , в ) , на концах которого значения функции f(x) имеют разные знаки . Для нахождения корня уравнения отрезок ( а, в ) делится пополам и вычисляется значение функции f (x) в точке z = ( а + в ) / 2 . Если f ( z ) = 0 , то z является корнем уравнения. Обычно в технических задачах можно удовлетвориться приближенным значением корня . Поэтому корнем уравнения можно считать и то значение z, при котором ½f( z ) ½£ e , где e - заранее назначенная малая величина , определяющая точность решения уравнения .
Если ½f( z )½> e, то рассматривается та половина отрезка ( а , z ) или
( z , в ) , на концах которой функция f (x) имеет разные знаки. Т.е. получают суженный отрезок ( а 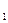 , в
, в 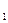 ) , где а
) , где а 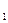 = а в
= а в 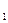 = z , или а
= z , или а 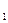 = z , в
= z , в 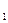 = в . Отрезок ( а
= в . Отрезок ( а 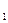 , в
, в 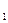 ) снова делится пополам и проводится то же рассмотрение , что и для первоначального отрезка . В результате на каком -то этапе получают или корень уравнения ( 1 ) , или последовательность вложенных друг в друга отрезков ( а
) снова делится пополам и проводится то же рассмотрение , что и для первоначального отрезка . В результате на каком -то этапе получают или корень уравнения ( 1 ) , или последовательность вложенных друг в друга отрезков ( а 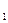 , в
, в 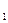 ) , ( а
) , ( а 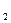 , в
, в 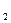 ) , . . ( а
) , . . ( а  , в
, в  ) ,таких ,что f(a
) ,таких ,что f(a  )
) 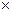 f ( в
f ( в  ) < 0 и в
) < 0 и в  - а
- а  = ( в - а ) / 2
= ( в - а ) / 2  (2)
(2)
Из формулы (2) видно ,что после n итераций (приближений ) разность в  - а
- а  может быть очень малой . Если ( в
может быть очень малой . Если ( в  - а
- а  ) £ 2 e , то координата середины отрезка и есть значение корня с требуемой точностью e .
) £ 2 e , то координата середины отрезка и есть значение корня с требуемой точностью e .
Метод половинного деления ( метод бисекций ) - простой и надежный метод поиска корня уравнения f ( x )= 0 . Он сходится для любых непрерывных функций . Скорость его сходимости невелика. Однако алго-ритм этого метода прост и легко реализуется на компьютерах (рис.2).
На основе разобранного выше алгоритма составлена подпрограмма типа S U B R O U T I N E с именем D E L P O . Входными параметрами этой подпрограммы являются границы отрезка (а,в). Подпрограмма D E L P O выдает значение корня уравнения, значение функции f(x), и количество итераций, сделанных для достижения заданной точности корня. Величина e , определяющая точность решения уравнения, вводится с клавиатуры . Ре-шаемое уравнение содержится во внешней функции F (x) , подпрограммы D E L P O . Текст подпрограммы представлен в приложении 2.
Исходные данные и результаты расчетов выводятся на экран дисплея и записываются в стандартный файл f t 0 7 f 0 0 1 на диск с помощью специиальной подпрограммы I D R E S, текст которой представлен в приложении 2 .
Таким образом , решение нелинейных уравнений методом бисекций можно свести к составлению главной программы, вызывающей три опи-санные выше подпрограммы , и составлению подпрограммы вычисления функции F ( x ). Образец главной программы приведен в приложении 2 .

Рис.2
