Решение СЛУ методом Жордана-Гаусса

Пример 4. Решить систему уравнений методом Жордана-Гаусса

.

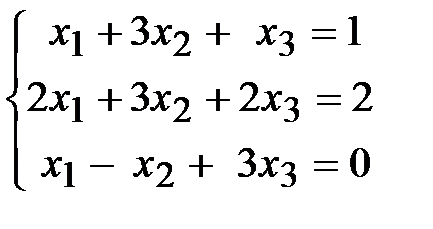Решение:Решая этим методом необходимо преобразовать расширенную матрицу системы так, чтобы привести к диагональному виду матрицу системы.

~ ~ ~

~ ~ ~ .

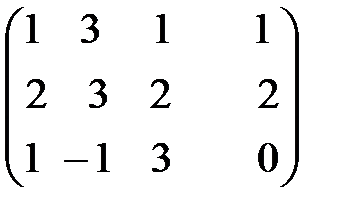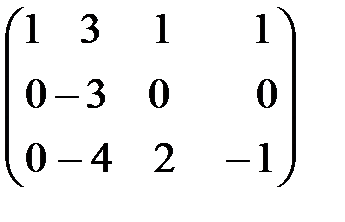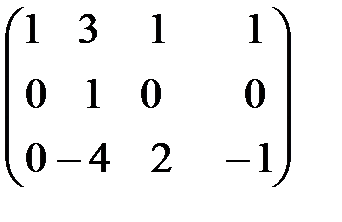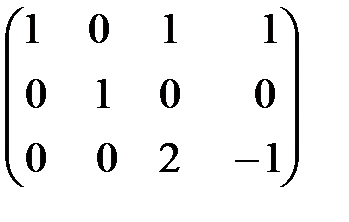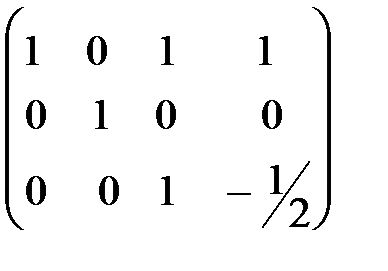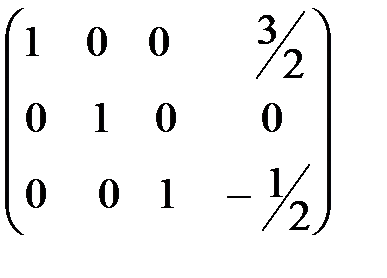Здесь вторая и третья матрицы получены, так же как и по методу Гаусса.

В четвертой матрице во втором столбце все элементы, кроме 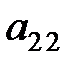, должны равняться нулю. Поэтому четвертая матрица получена из третьей следующим образом: элементы второй строки умножаются на -3 и прибавляются к первой; элементы второй строки умножаются на 4 и прибавляются к третьей. Далее элементы третьей строки в четвертой матрице умножаются на 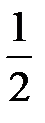, чтобы элемент 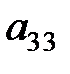стал равен 1. Так получили пятую матрицу. Теперь нужно добиться, чтобы элементы третьего столбца, все кроме 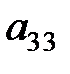стали равны 0. Следует заметить, что элемент 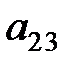уже равен 0, поэтому вторую строку не преобразовываем, а к первой прибавляем третью, умноженную на -1, тем самым получаем шестую матрицу, где на месте матрицы системы (три первых столбца) расположении диагональная, а именно – единичная 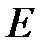матрица. Восстановив систему по последней матрице,

сразу получаем решение: .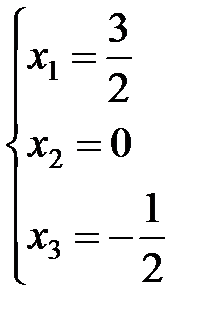

Решения, полученные всеми методами совпадают. Ответ: .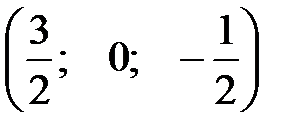

Замечание. Решение можно было оформлять в виде таблицы (смотри далее пример 6).

Решение систем 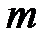линейных уравнений с 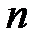переменными

Для решения таких СЛУ предпочтительнее применять метод Жордана-Гаусса, т.к. в процессе решения исследуется система.

Пример 5. Решить систему уравнений методом Жордана-Гаусса

.

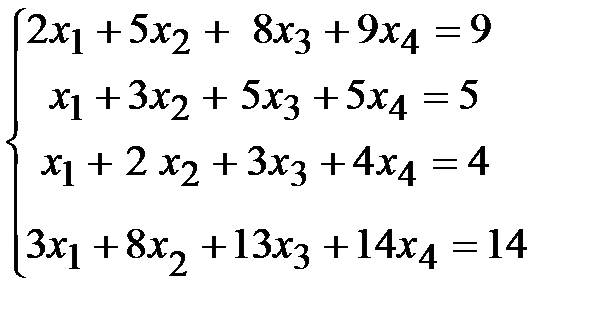Решение:Запишем расширенную матрицу СЛУ и приведем ее к диагональному виду:

~ ~

~ ~ ~ .

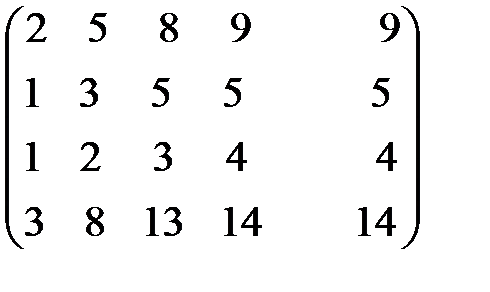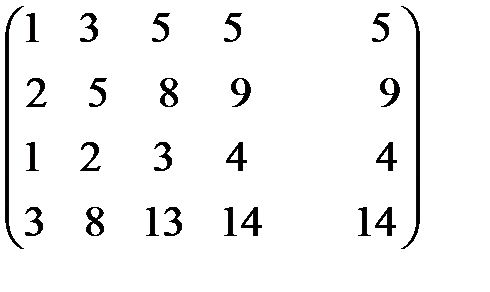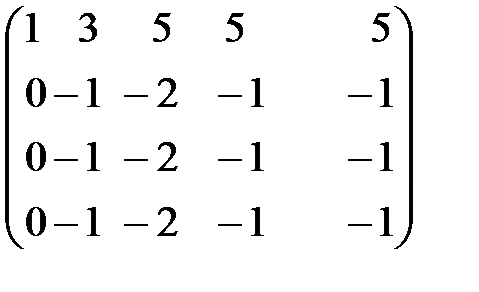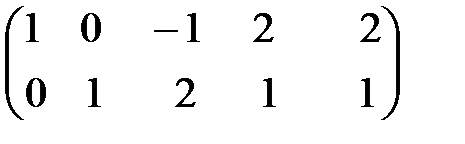Число оставшихся уравнений равно 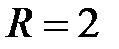, а число переменных 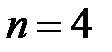, следовательно, система неопределенна, т.е. имеет бесконечно много решений.

Запишем систему по виду последней матрицы:

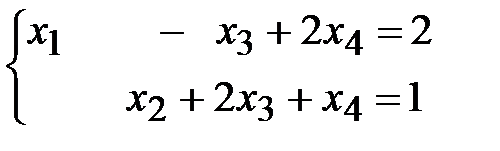
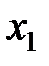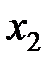Переменные, которые встречаются только в одном уравнении с коэффициентом равным единице, являются базисными. В данном примере и , оставшиеся – свободные, т.е. 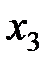и 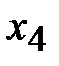. Выразим базисные переменные через свободные, получим общее решение СЛУ:

.

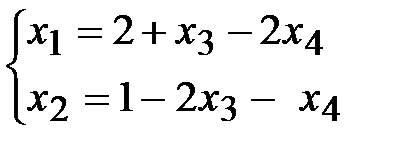Придавая произвольные значения свободным переменным будем получать частные решения. Другими словами, если 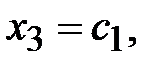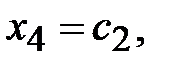тогда 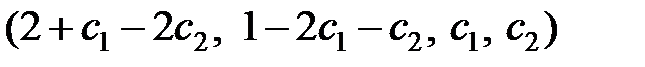- общее решение системы.

Найдем какое-нибудь частное решение системы. Пусть, например, 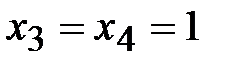, тогда 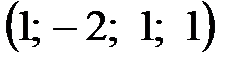– частное решение системы.

Частных решений можно выписать бесконечно много.

Пусть свободные переменные 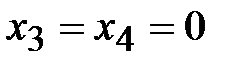, тогда 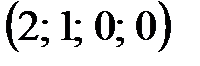- базисное решение системы. Оно является допустимым и невырожденным.

Можно найти другие базисные решения, выбирая в качестве базисных, другие пары переменных. Число базисных решений конечно.

Пример 6.Решить систему уравнений с помощью таблиц Гаусса

.

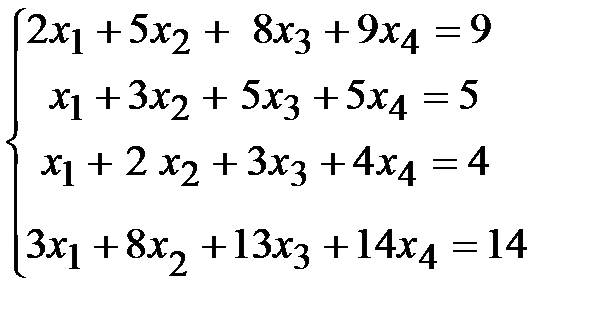Решение:Запишем данную систему в таблицу Гаусса (Т.1). Выберем в ней ведущий элемент (в таблице отмечен [ 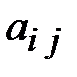]). На первом шаге им может быть любой ненулевой, например 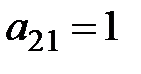. Заполняем таблицу 2 (Т.2), применяя правило прямоугольника, а именно: заполнение начинаем с ведущей (в данном случае – второй) строки. В таблицу 2 выписываются элементы ведущей строки из предыдущей таблицы, деленные на ведущий элемент. Все элементы ведущего столбца (первого), кроме ведущего который стал равен единице, обнуляются. В столбец «б. п.» в ведущей строке (второй) записывается название ведущего столбца – 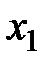. Остальные элементы пересчитываем по правилу прямоугольника. Например, чтобы вычислить значение элемента 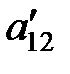вернемся в предыдущую таблицу 1 и мысленно нарисуем прямоугольник так, чтобы пересчитываемый элемент 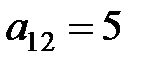и ведущий 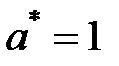располагались на одной его диагонали, тогда на другой диагонали будут располагаться элементы 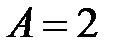и 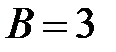. Подставим в формулу (1.13): 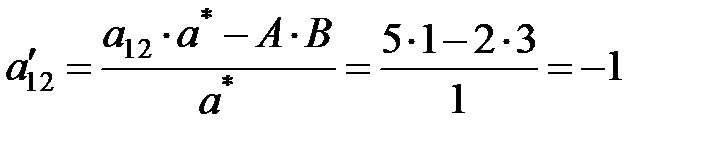, который записываем в таблице 2 на пересечении первой строки и второго столбца. Другой пример: вычислим значение элемент 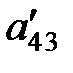в таблице 2. Для этого вернемся в таблицу 1 и мысленно нарисуем прямоугольник так, чтобы пересчитываемый элемент 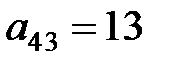и ведущий 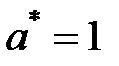располагались на одной его диагонали, тогда на другой диагонали располагаются элементы 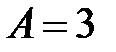и 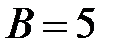. Подставим в формулу и найдем: 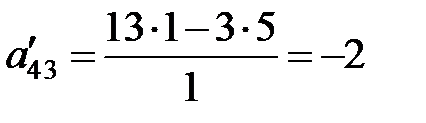, который записан в таблице 2 на пересечении четвертой строки и третьего столбца. Подобным образом пересчитываются все элементы, кроме тех, что расположены в ведущей строке и столбце.

б.п.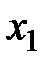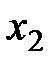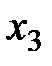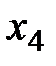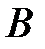
	[1]					Т.1
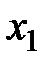		[-1] -1 -1	-2 -2 -2	-1 -1 -1	-1 -1 -1	Т.2
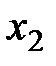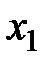			-1	[1]		Т.3
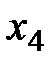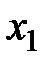		-2	-5			Т.4

В таблице 2 выбираем ведущий элемент – любой ненулевой, только не во второй строке (она была ведущей), например 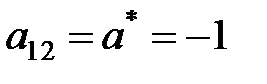. Заполняем таблицу 3 (Т.3), начиная с ведущей строки, записывая элементы первой (ведущей) строки из предыдущей таблицы, деленные на ведущий элемент равный -1. Все элементы ведущего столбца (второго), кроме ведущего который стал равен единице, обнуляются. В столбец «б. п.» в ведущей строке (первой) записывается название ведущего столбца – 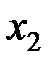. Аналогично по правилу прямоугольника пересчитываем остальные элементы. Итак, после пересчета осталось две строки (две последние, нулевые удаляем). Базисных переменных тоже две 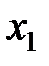и 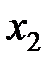, т.е. столбец «б.п» заполнен. Теперь можно выписать базисное решение, соответствующее третьей таблице (Т.3), причем значения «б.п.» определяются из столбца свободных членов 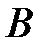: (2,1,0,0), которое является невырожденным и допустимым.Чтобы найти другое базисное решение, нужно в Т. 3 выбрать ведущий элемент, например 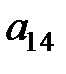и пересчитать следующую таблицу, в нашем примере четвертая (Т.4). Базисное решение, выписанное по таблице 4: (0,0,0,1) – допустимое и вырожденное.

Количество базисных решений конечно, поэтому можно найти все базисные решения.

Ясно, что каждой таблице соответствует, эквивалентная исходной, система. Можно восстановить по таблице 3 или 4 систему и записать общие решения, но их вид будет разным.

Задачи с экономическим содержанием

Понятие матриц широко применяется при решении практических задач. Применяя известные действия с матрицами, можно определить объемы производства или продаж за несколько отчетных периодов, прирост производства или продаж по сравнению с предыдущим периодом, выручку, стоимость затрат и т.п.

Пример 7.В трех магазинах продаются два типа продукции. Матрицы 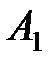, 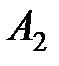и 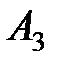– объемы продаж этой продукции в магазинах в первом, втором и третьем месяцах соответственно (усл. ед.). Цена реализации одной условной единицы первого и второго типа продукции задана матрицей 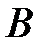(ден. ед.). Определить: 1) матрицу 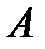- объем продаж за квартал; 2) матрицу - прирост продаж за третий месяц по сравнению со вторым; 3) выручку каждого магазина за квартал. Проанализировать результаты.

, , , .

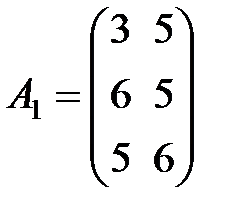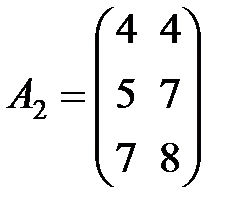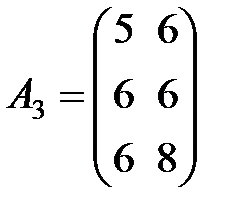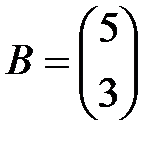Решение:

1) Объем продаж за квартал – есть сумма матриц 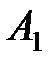, 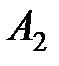и 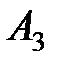, т.е.

= + + = .

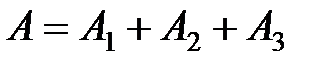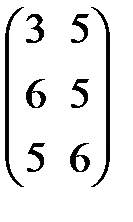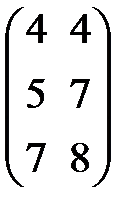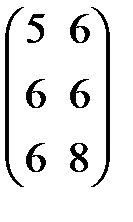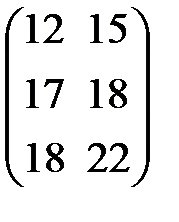Итак, первый магазин продаст продукции первого типа за квартал на 12 усл. ед., второго типа на 15 усл. ед. Объем продаж второго магазина за квартал продукции первого и второго типа составит соответственно 17 и 18 усл. ед., а третьего 18 и 22 усл.ед.

2) Прирост в третьем месяце по сравнению со вторым для трех магазинов определяется разностью матриц 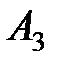и 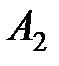, причем положительные элементы показывают, что объем продаж увеличился, отрицательные – уменьшился, нулевые – не изменился.

= – = .

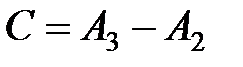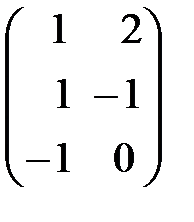Итак, в третьем месяце по сравнению со вторым в первом магазине объем продаж продукции первого типа увеличился на 1усл. ед. второго типа – на 2. Второй магазин в третьем месяце объем продаваемой продукции первого типа увеличил на 1 усл. ед., а продукции второго типа продал на 1 усл. ед. меньше, чем во втором месяце. У третьего магазина уменьшился объем продаваемой продукции первого типа на 1 усл. ед., а второго типа – не изменился.

3) Выручка каждого магазина за квартал определяется матрицей .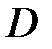

= .

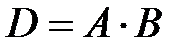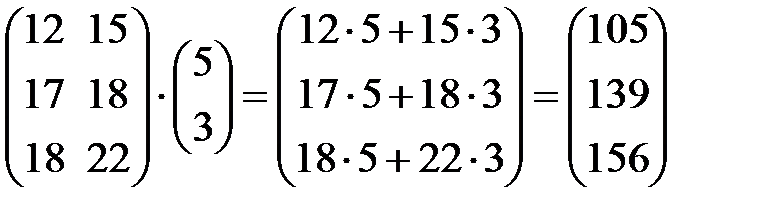Итак, выручка от реализации всей продукции за квартал для первого магазина составила 105 ден. ед., для второго – 139 ден. ед. и для третьего – 156 ден. ед.

Пример 8.Обувная фабрика специализируется по выпуску изделий трех видов: сапог, кроссовок и ботинок; при этом ежедневно используется сырье трех типов: 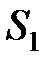, 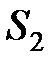и 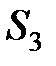, которое должно быть израсходовано полностью. Нормы расхода каждого из них на изготовление одной пары обуви и объем расхода сырья за один день заданы в таблице.

Вид сырья	Нормы расхода сырья на изготовление одной пары, усл.ед.	Расход сырья за один день, усл.ед.
сапог	кроссовок	ботинок

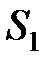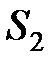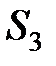Необходимо:

1) составить систему уравнений для нахождения ежедневного объема выпуска каждого вида обуви;

2) решить эту систему по формулам Крамера;

3) решить систему матричным методом;

4) решить систему, применяя таблицы Гаусса.

Решение:Введем обозначения: пусть ежедневно фабрика выпускает 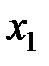пар сапог, 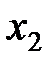пар кроссовок и 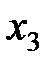пар ботинок.

1) в соответствии с расходом сырья каждого вида получим систему:

.

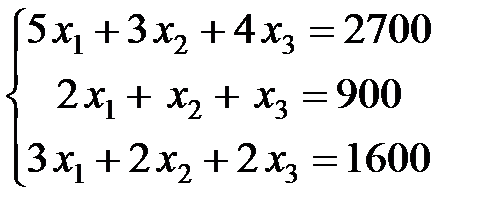2) для решения этой системы по формулам Крамера составим и вычислим определители:

;

;

;

.

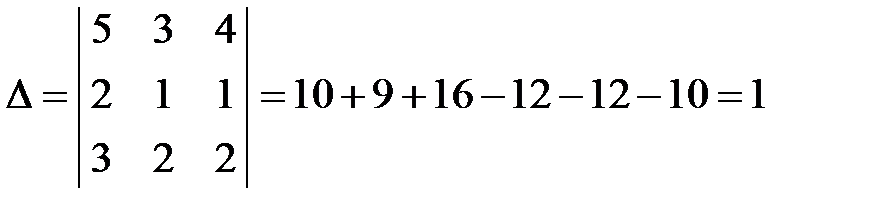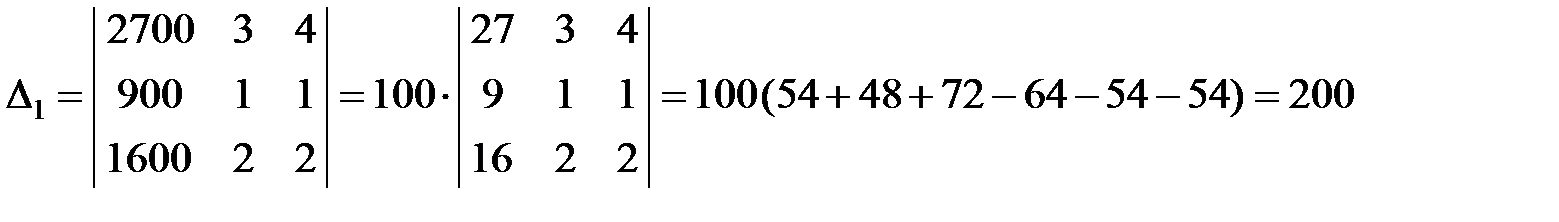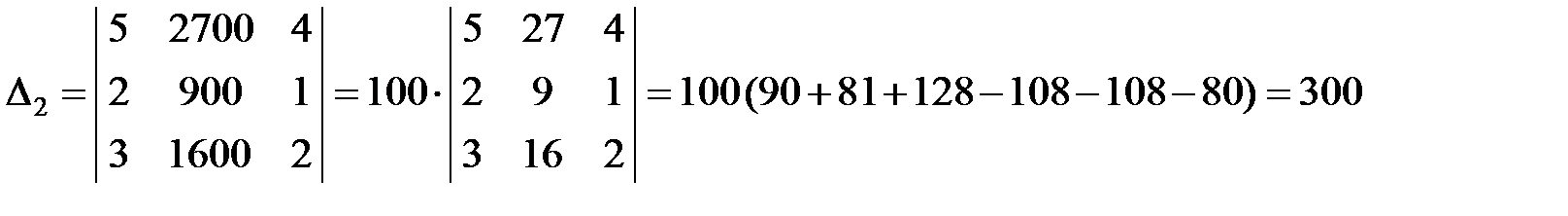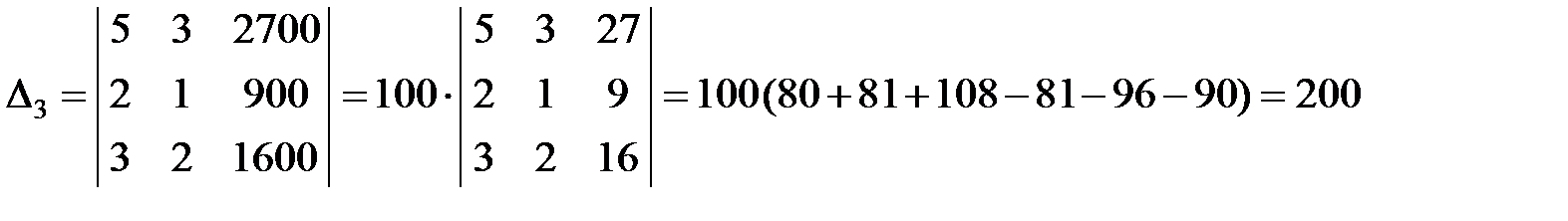Замечание. При вычислении определителей 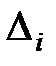применяли свойство 5⁰.

Найдем решение системы по формулам (2.7):

; ; .

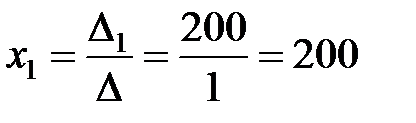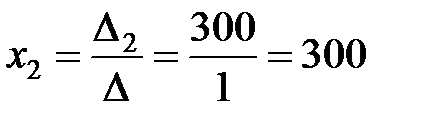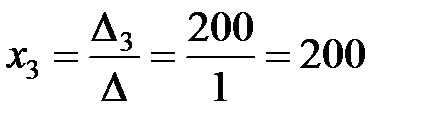Следовательно, решение системы имеет вид: (200; 300; 200).

3) для данной системы уравнений матрица системы ,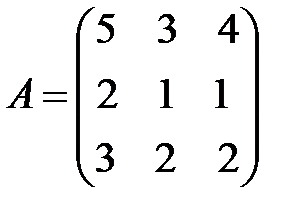

матрицы-столбцы свободных членов 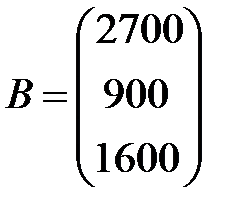и неизвестных .

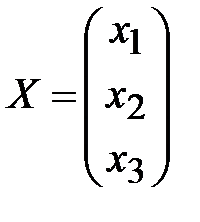Для нахождения решения по формуле (2.6), необходимо найти для матрицы 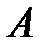обратную. Выполним все четыре пункта алгоритма нахождения :

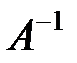1. ;

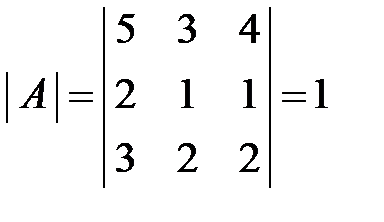2. ;

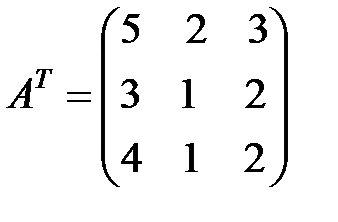3. Найдем алгебраические дополнения для всех элементов :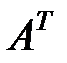

.

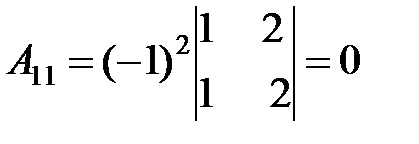
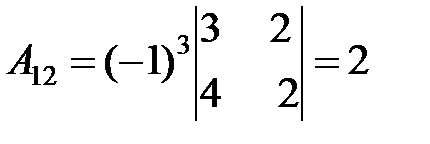
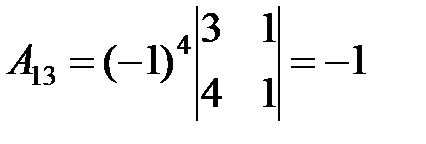
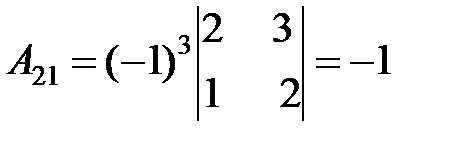
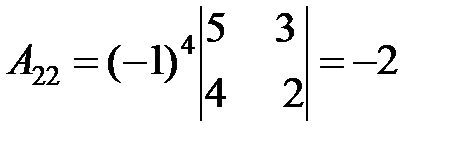
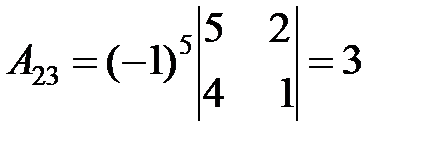
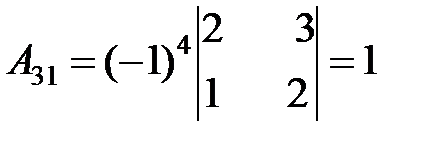
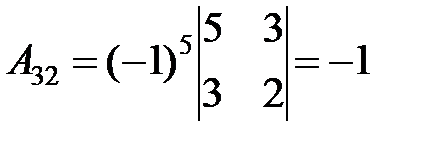
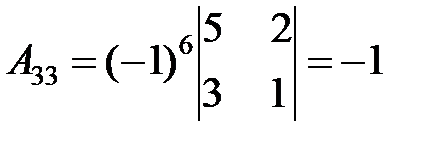Итак, присоединенная матрица имеет вид: .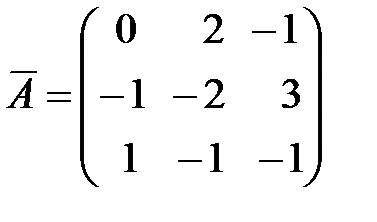

4. Вычислим обратную матрицу по формуле (1.5): :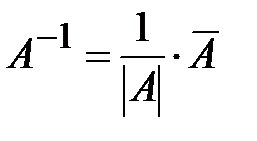

.

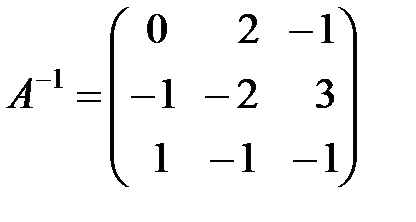Следовательно, решение = .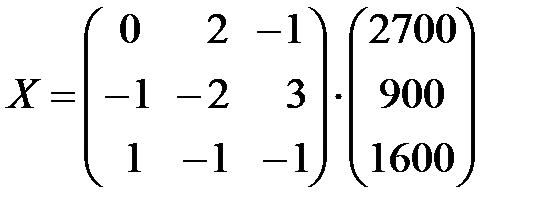

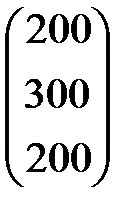Итак, 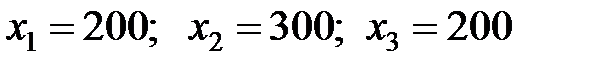, или .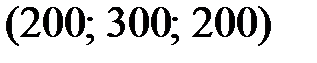

4) заполним первую таблицу Гаусса (Т.1), используя коэффициенты при неизвестных системы и столбец свободных членов уравнений. Поскольку решение единственное, то столбец «б. п.» следует опустить.

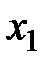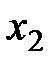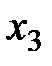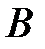	[1]			Т.1
-1 -1		[1]	-200	Т.2
-1 [-1]			-200	Т.3
				Т.4

Отсюда, восстановив систему по Т.4, получим:

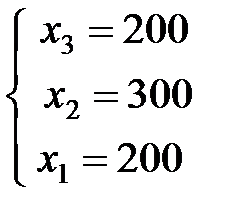или (200; 300; 200).

Итак, фабрика выпускает 200 пар сапог, 300 пар кроссовок и 200 пар ботинок.