КОНТРОЛЬНАЯ РАБОТА № 8
Контрольная работа № 8 состоит из пяти задач. Ниже рассмотрены варианты решения заданий.
Образец выполнения задания № 1
Задача.Исследовать на сходимость числовой ряд 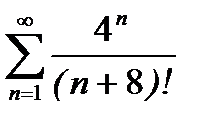 .
.
Решение.Проверяем сходимость ряда по признаку Даламбера. Имеем
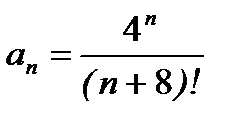 , отсюда
, отсюда 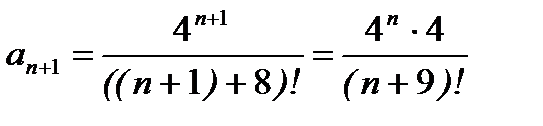 ,
,
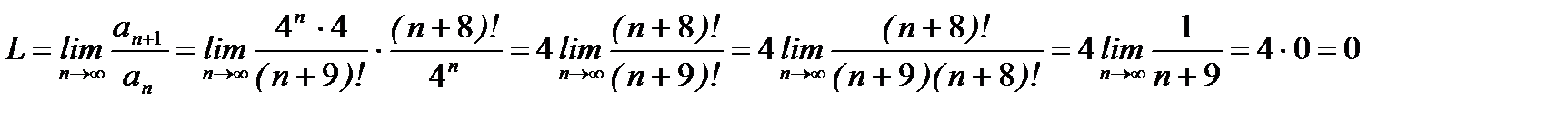
Получилось 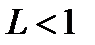 , следовательно, наш ряд сходится.
, следовательно, наш ряд сходится.
Образец выполнения задания № 2
Задача.Найти интервал сходимости степенного ряда 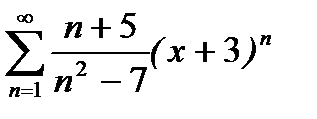 .
.
Решение. Имеем
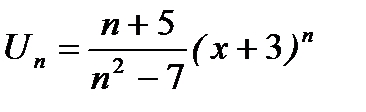 , отсюда
, отсюда 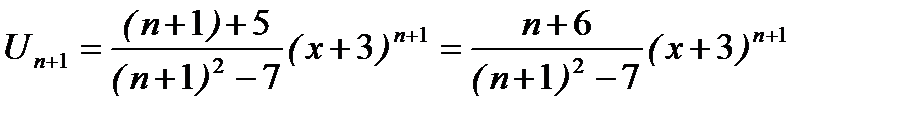 ,
,
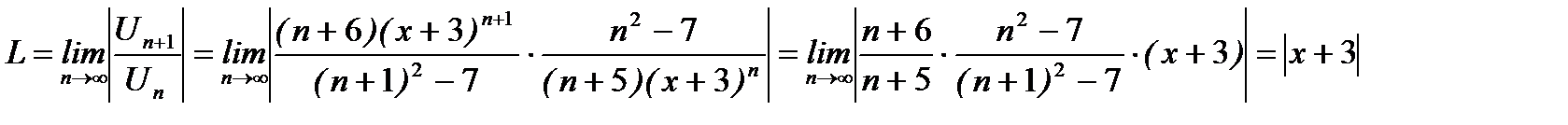 .
.
Потребуем, чтобы было 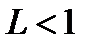 ; тогда
; тогда 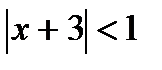 ,
, 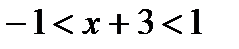 ,
, 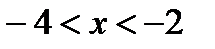 . Таким образом, внутри интервала
. Таким образом, внутри интервала 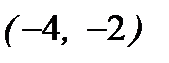 исходный ряд сходится абсолютно. Исследуем сходимость на концах этого интервала.
исходный ряд сходится абсолютно. Исследуем сходимость на концах этого интервала.
При 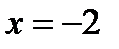 исходный ряд становится числовым:
исходный ряд становится числовым: 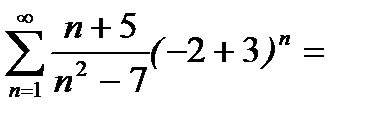
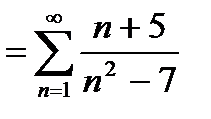 ; сравним этот ряд с рядом
; сравним этот ряд с рядом 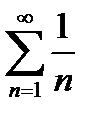 , который расходится:
, который расходится:
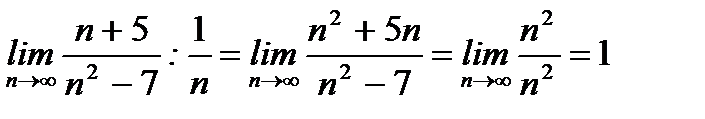 - получилось число больше 0, поэтому ряд
- получилось число больше 0, поэтому ряд 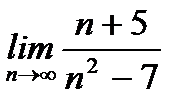 подобен ряду
подобен ряду 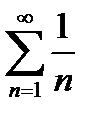 , т.е. расходится.
, т.е. расходится.
При 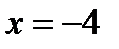 исходный ряд становится таким:
исходный ряд становится таким: 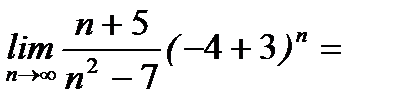
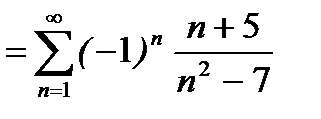 - знакочередующийся ряд, который нужно исследовать по признаку Лейбница. Сравним
- знакочередующийся ряд, который нужно исследовать по признаку Лейбница. Сравним 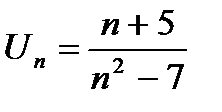 с
с 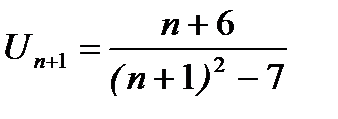 :
:
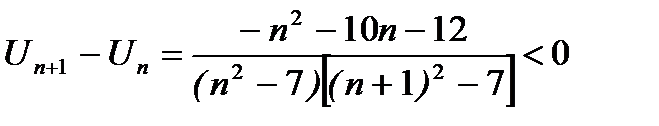 при больших
при больших 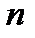 ; таким образом
; таким образом 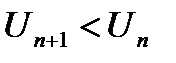 , т.е. члены ряда уменьшаются по абсолютной величине. Кроме того,
, т.е. члены ряда уменьшаются по абсолютной величине. Кроме того, 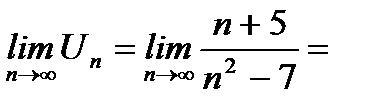
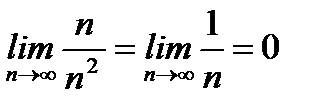 , т.е. члены ряда стремятся к 0. Следовательно, знакочередующийся ряд сходится. Таким образом,
, т.е. члены ряда стремятся к 0. Следовательно, знакочередующийся ряд сходится. Таким образом, 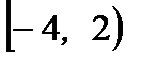 - интервал сходимости исходного степенного ряда.
- интервал сходимости исходного степенного ряда.
Образец выполнения задания № 3
Задача.Вычислить интеграл 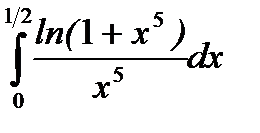 с точностью до
с точностью до 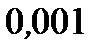 путем предварительного разложения подынтегральной функции в ряд.
путем предварительного разложения подынтегральной функции в ряд.
Решение. Применим формулу разложения в ряд 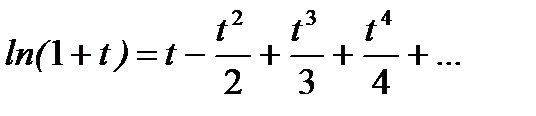
Тогда 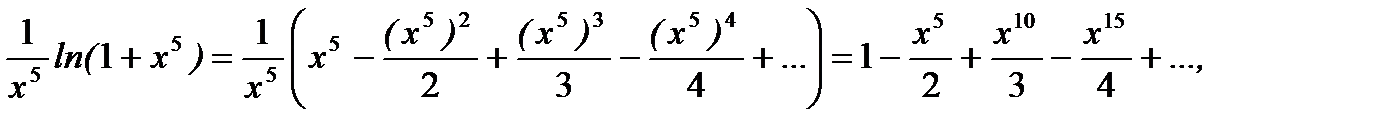
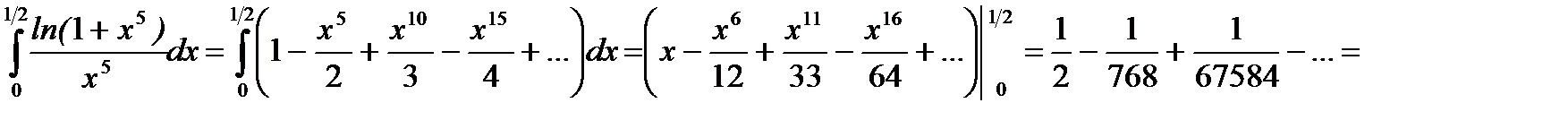
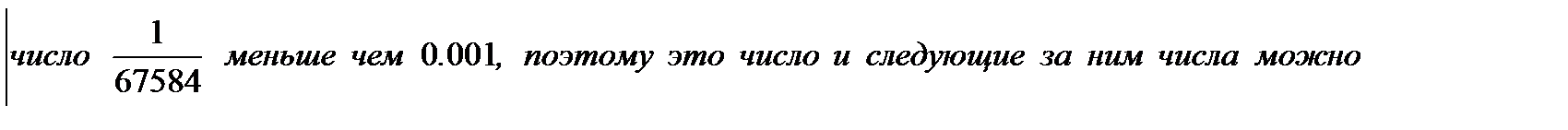
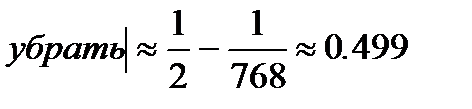 .
.
Образец выполнения задания № 4
Задача.Найти три первых отличных от нуля члена разложения в степенной ряд функции 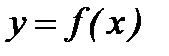 , являющейся частным решением дифференциального уравнения
, являющейся частным решением дифференциального уравнения 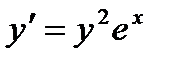 ,
, 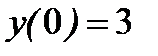 .
.
Решение. Искомое решение имеет вид
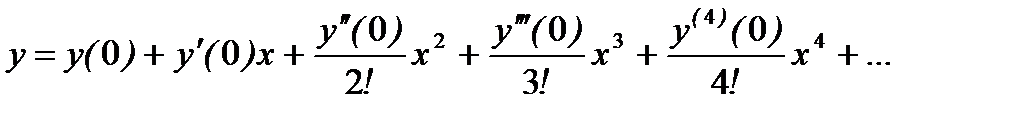 (А)
(А)
Имеем 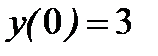
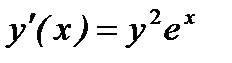 , отсюда
, отсюда 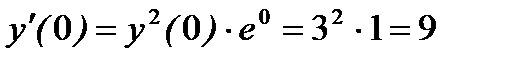
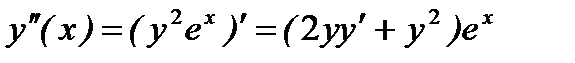 , отсюда
, отсюда 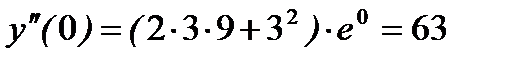
Подставив эти значения в (А), получим ответ
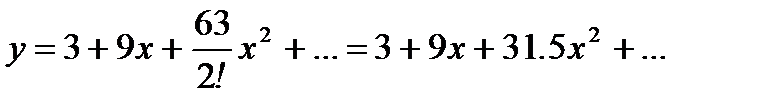
Образец выполнения задания № 5
Задача.Функцию 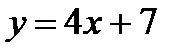 в интервале (0, 3) разложить в ряд: а) косинусов, б) синусов.
в интервале (0, 3) разложить в ряд: а) косинусов, б) синусов.
Решение.а) Разложение в ряд косинусов имеет вид 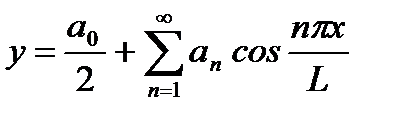 , где
, где 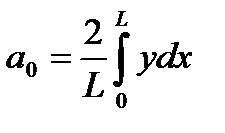 ,
, 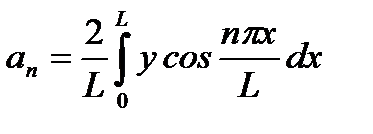 .
.
В нашем случае интервал (0, 3) имеет длину 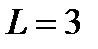 , поэтому
, поэтому
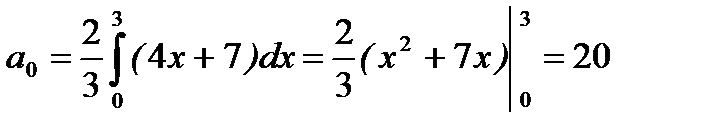 ,
, 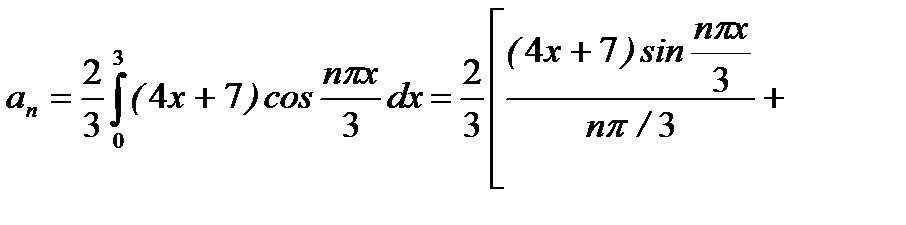
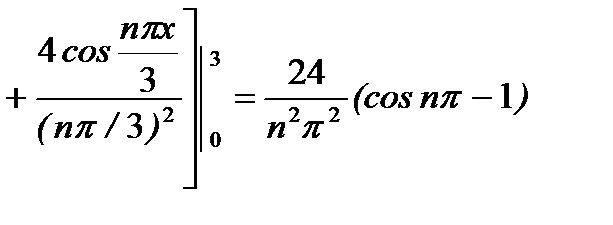 . Поэтому
. Поэтому 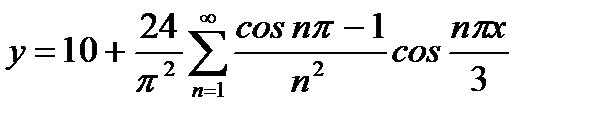 .
.
Это выражение можно упростить, если заметить, что
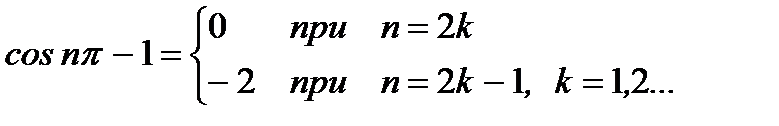
Тогда 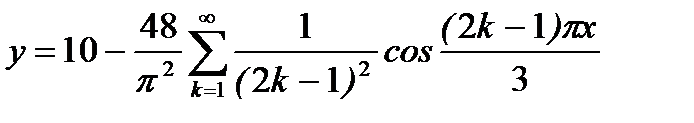 .
.
б) Разложение в ряд синусов имеет вид 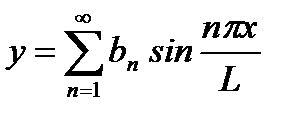 , где
, где
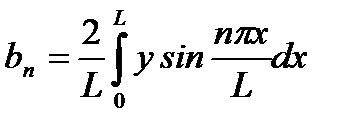 .
.
В нашем случае 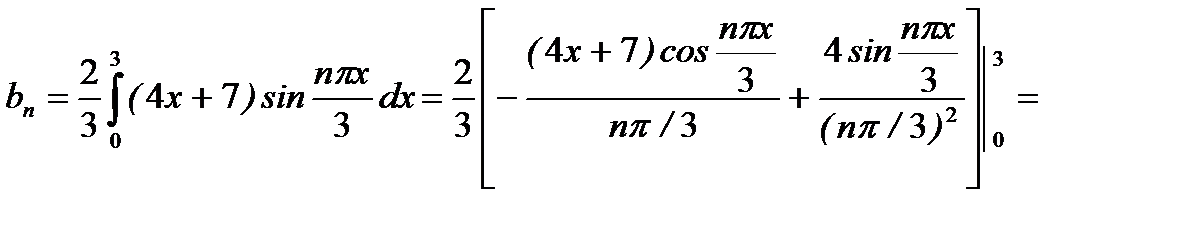
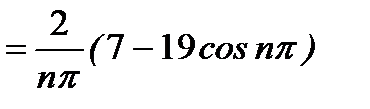 .
.
Поэтому 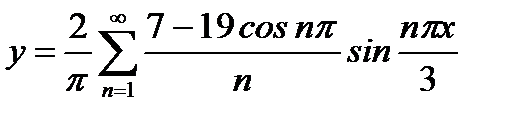 . Ввиду того, что
. Ввиду того, что 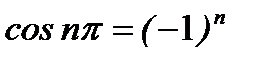 , это равенство можно записать так:
, это равенство можно записать так: 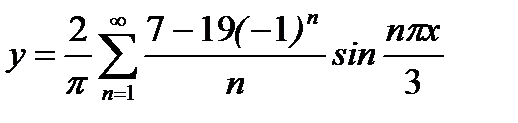 .
.
ЗАДАНИЯ К КОНТРОЛЬНОЙ РАБОТЕ № 8
Задание № 1
Исследовать на сходимость ряд.
1. 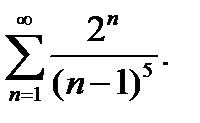
2. 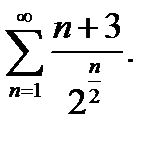
3. 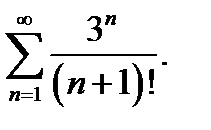
4. 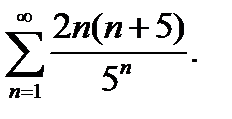
5. 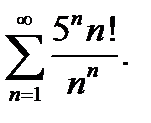
6. 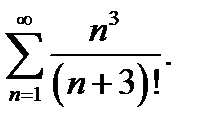
7. 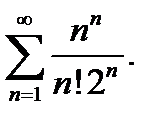
8. 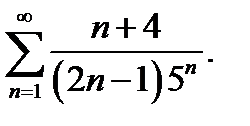
9. 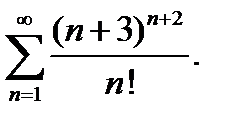
10. 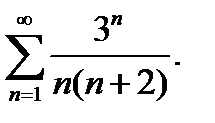
11. 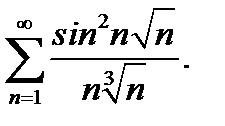
12. 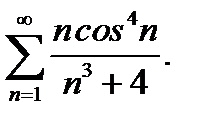
13. 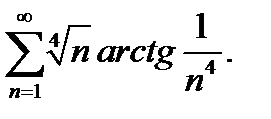
14. 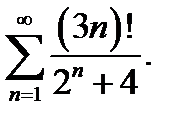
15. 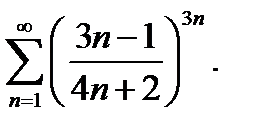
16. 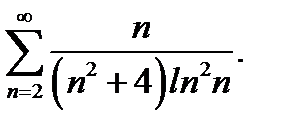
17. 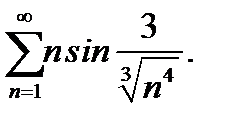
18. 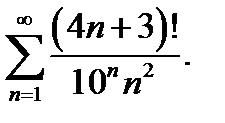
19. 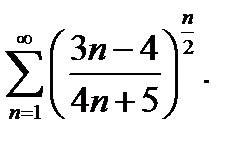
20. 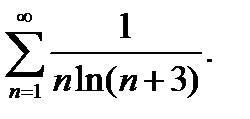
21. 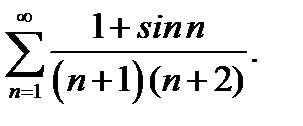
22. 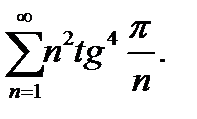
23. 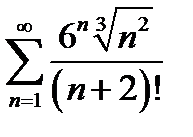
24. 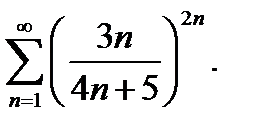
25. 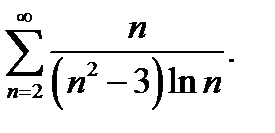
26. 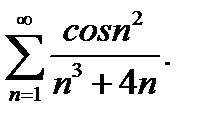
27. 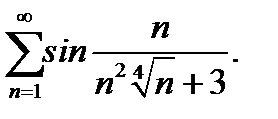
28. 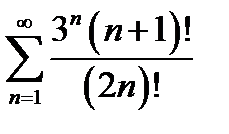
29. 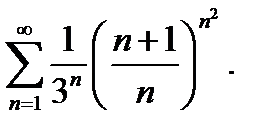
30. 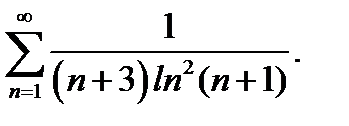
Задание № 2
Определить интервал сходимости рядов.
1. 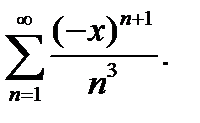
2. 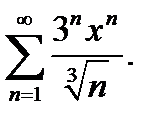
3. 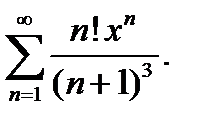
4. 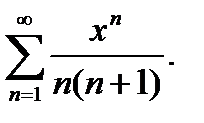
5. 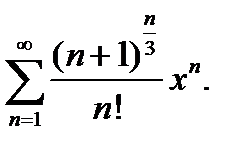
6. 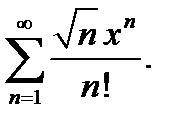
7. 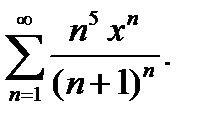
8. 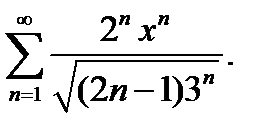
9. 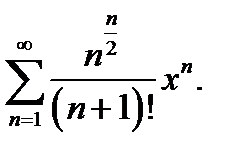
10. 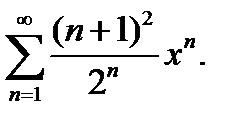
11. 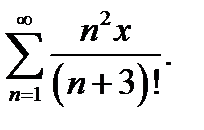
12. 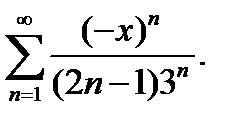
13. 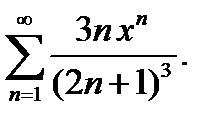
14. 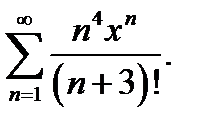
15. 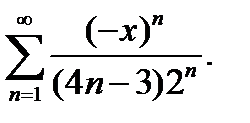
16. 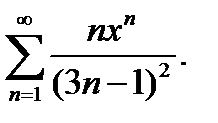
17. 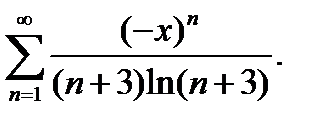
18. 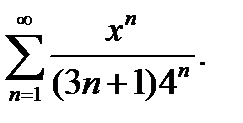
19. 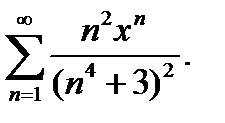
20. 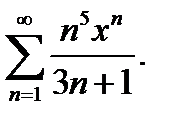
21. 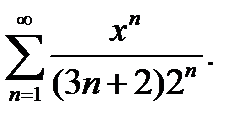
22. 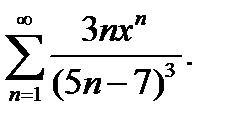
23. 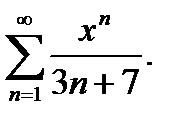
24. 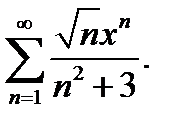
25. 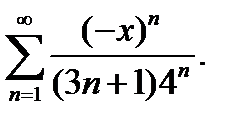
26. 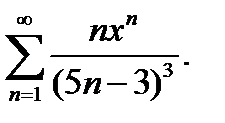
27. 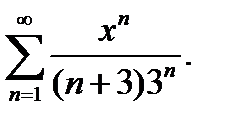
28. 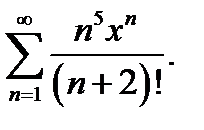
29. 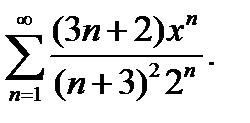
30. 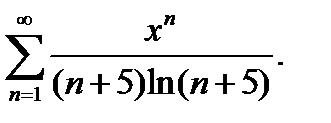
Задание № 3
Вычислить определенный интеграл с точностью до 0,001. С этой целью подынтегральную функцию следует разложить в ряд и затем почленно проинтегрировать.
1. 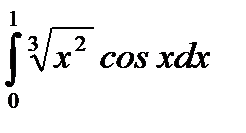 .
.
2. 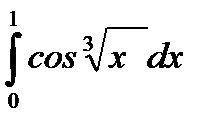 .
.
3. 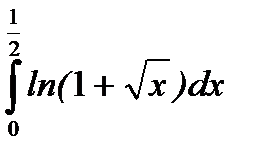 .
.
4. 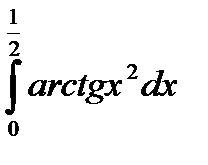 .
.
5. 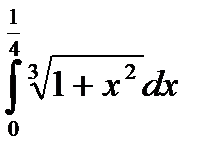 .
.
6. 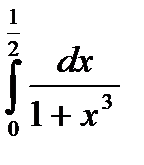 .
.
7. 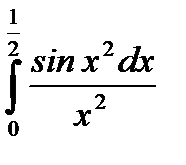 .
.
8. 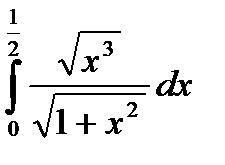 .
.
9. 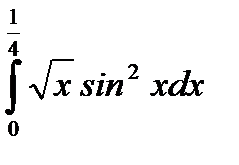 .
.
10. 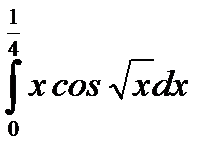 .
.
11. 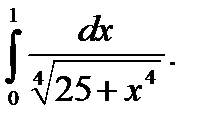
12. 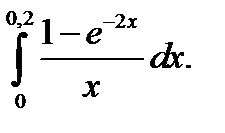
13. 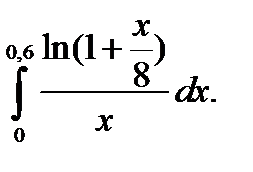
14. 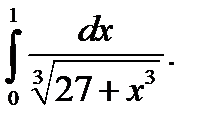
15. 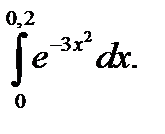
16. 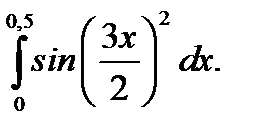
17. 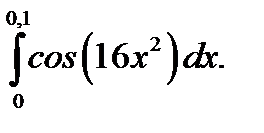
18. 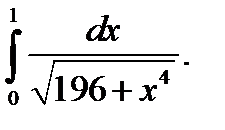
19. 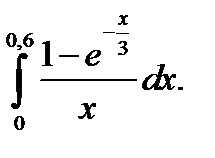
20. 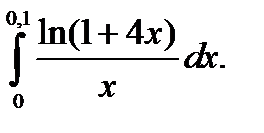
21. 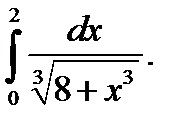
22. 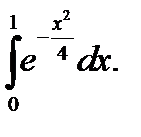
23. 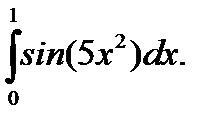
24. 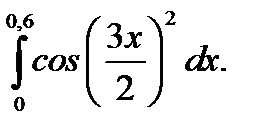
25. 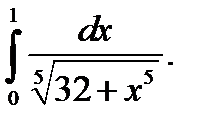
26. 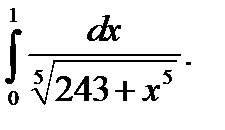
27. 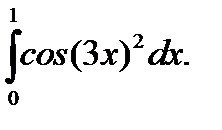
28. 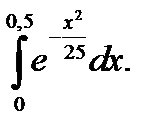
29. 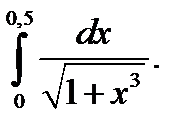
30. 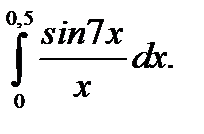
Задание № 4
Найти три первых отличных от нуля члена разложения в степенной ряд интеграла 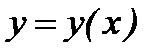 дифференциального уравнения, удовлетворяющего заданному начальному условию.
дифференциального уравнения, удовлетворяющего заданному начальному условию.
1. 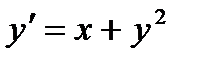 при
при 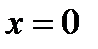 ,
, 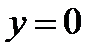 .
.
2. 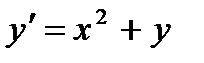 при
при 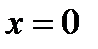 ,
, 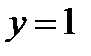 .
.
3. 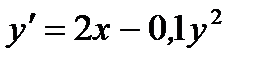 при
при 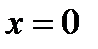 ,
, 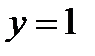 .
.
4. 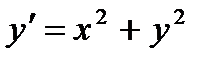 при
при 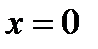 ,
, 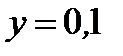 .
.
5. 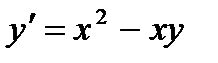 при
при 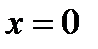 ,
, 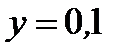 .
.
6. 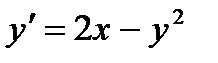 при
при 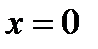 ,
, 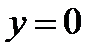 .
.
7. 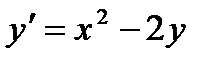 при
при 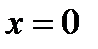 ,
, 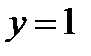 .
.
8. 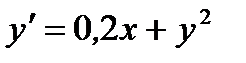 при
при 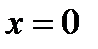 ,
, 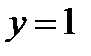 .
.
9. 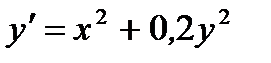 при
при 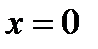 ,
, 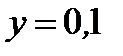 .
.
10. 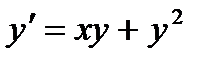 при
при 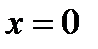 ,
, 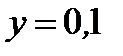 .
.
11. 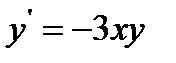 при
при 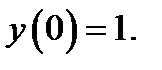
12. 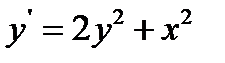 при
при 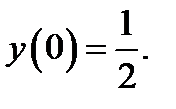
13. 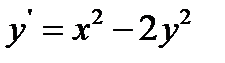 при
при 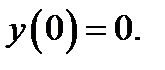
14. 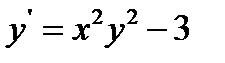 при
при 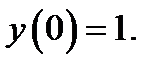
15. 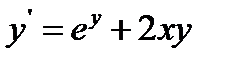 при
при 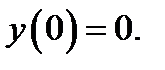
16. 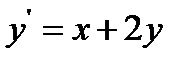 при
при 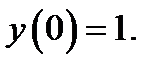
17. 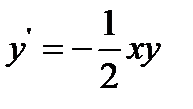 при
при 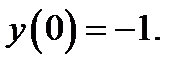
18. 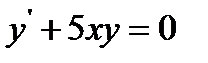 при
при 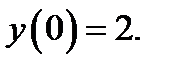
19. 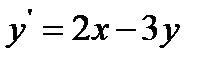 при
при 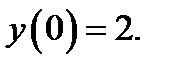
20. 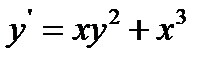 при
при 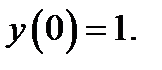
21. 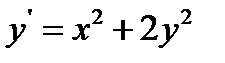 при
при 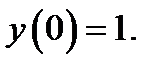
22. 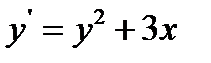 при
при 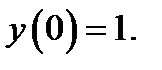
23. 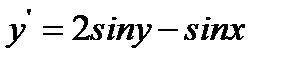 при
при 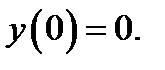
24. 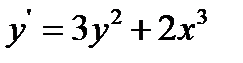 при
при 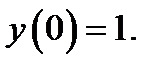
25. 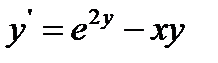 при
при 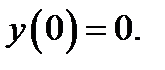
26. 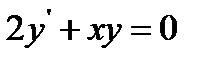 при
при 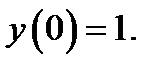
27. 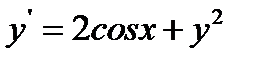 при
при 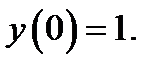
28. 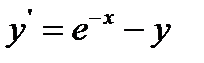 при
при 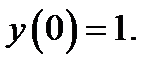
29. 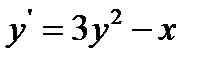 при
при 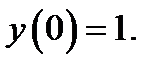
30. 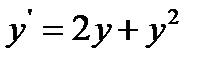 при
при 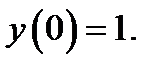
Задание № 5
1. Функцию 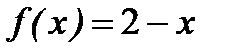 в интервале (0, 2) разложить в ряд косинусов.
в интервале (0, 2) разложить в ряд косинусов.
2. Функцию 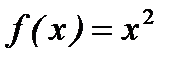 в интервале (0,
в интервале (0, 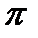 ) разложить в ряд косинусов.
) разложить в ряд косинусов.
3. Функцию 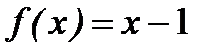 в интервале (0, 1) разложить в ряд синусов.
в интервале (0, 1) разложить в ряд синусов.
4. Функцию 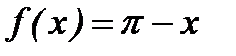 в интервале (0,
в интервале (0, 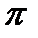 ) разложить в ряд синусов.
) разложить в ряд синусов.
5. Функцию 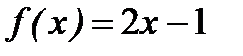 в интервале (0, 1) разложить в ряд косинусов.
в интервале (0, 1) разложить в ряд косинусов.
6. Функцию 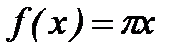 в интервале (0,
в интервале (0, 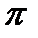 ) разложить в ряд косинусов.
) разложить в ряд косинусов.
7. Функцию 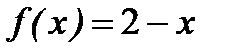 в интервале (0, 2) разложить в ряд синусов.
в интервале (0, 2) разложить в ряд синусов.
8. Функцию 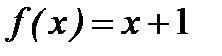 в интервале (0, 1) разложить в ряд синусов.
в интервале (0, 1) разложить в ряд синусов.
9. Функцию 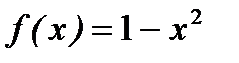 в интервале (0, 1) разложить в ряд синусов.
в интервале (0, 1) разложить в ряд синусов.
10. Функцию 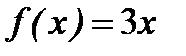 в интервале (0, 1) разложить в ряд синусов.
в интервале (0, 1) разложить в ряд синусов.
11. Функцию 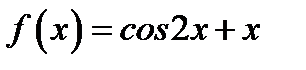 в интервале
в интервале 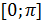 разложить в ряд косинусов.
разложить в ряд косинусов.
12. Функцию 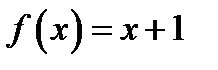 в интервале
в интервале 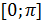 разложить в ряд синусов.
разложить в ряд синусов.
13. Функцию 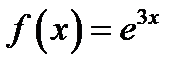 в интервале
в интервале 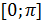 разложить в ряд косинусов.
разложить в ряд косинусов.
14. Функцию 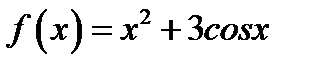 в интервале
в интервале 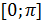 разложить в ряд синусов.
разложить в ряд синусов.
15. Функцию 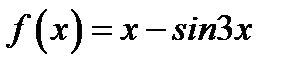 в интервале
в интервале 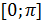 разложить в ряд косинусов.
разложить в ряд косинусов.
16. Функцию 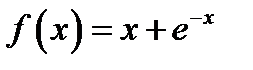 в интервале
в интервале 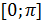 разложить в ряд синусов.
разложить в ряд синусов.
17. Функцию 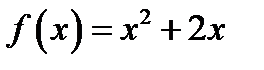 в интервале
в интервале 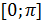 разложить в ряд косинусов.
разложить в ряд косинусов.
18. Функцию 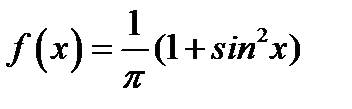 в интервале
в интервале 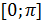 разложить в ряд синусов.
разложить в ряд синусов.
19. Функцию 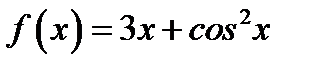 в интервале
в интервале 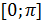 разложить в ряд косинусов.
разложить в ряд косинусов.
20. Функцию 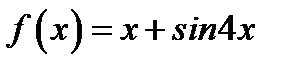 в интервале
в интервале 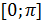 разложить в ряд синусов.
разложить в ряд синусов.
21. Функцию 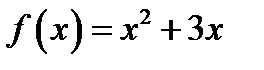 в интервале
в интервале 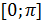 разложить в ряд косинусов.
разложить в ряд косинусов.
22. Функцию 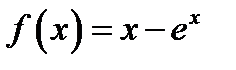 в интервале
в интервале 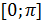 разложить в ряд синусов.
разложить в ряд синусов.
23. Функцию 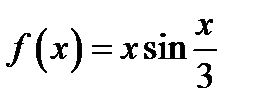 в интервале
в интервале 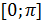 разложить в ряд косинусов.
разложить в ряд косинусов.
24. Функцию 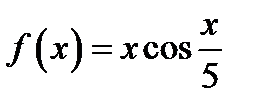 в интервале
в интервале 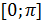 разложить в ряд синусов.
разложить в ряд синусов.
25. Функцию 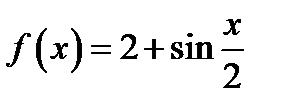 в интервале
в интервале 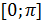 разложить в ряд косинусов.
разложить в ряд косинусов.
26. Функцию 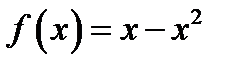 в интервале
в интервале 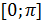 разложить в ряд синусов.
разложить в ряд синусов.
27. Функцию 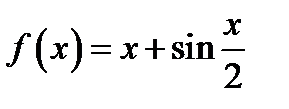 в интервале
в интервале 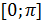 разложить в ряд косинусов.
разложить в ряд косинусов.
28. Функцию 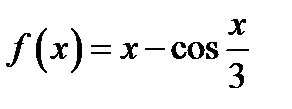 в интервале
в интервале 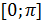 разложить в ряд синусов.
разложить в ряд синусов.
29. Функцию 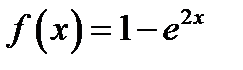 в интервале
в интервале 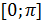 разложить в ряд косинусов.
разложить в ряд косинусов.
30. Функцию 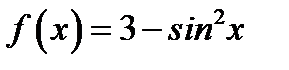 в интервале
в интервале 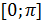 разложить в ряд синусов.
разложить в ряд синусов.
СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ
1. Данко П.Е., Попов А.Г. Высшая математика в упражнениях и задачах. В 2 ч. Ч. 2. Учебное пособие для вузов. – 6-е изд. – М.: Издательский дом «ОНИКС 21 век»: Мир и Образование, 2003. – 416 с.
2. Берман Г.Н. Сборник задач по курсу математического анализа: Учеб. пособие. – 22-е изд., перер. – СПб.: Изд-во «Профессия», 2006. – 432 с.: ил.
3. Ефимов Н.В. Краткий курс аналитической геометрии: Учеб. Пособие. – 13-е изд., смер. – М.: ФИЗМАТЛИТ, 2005. – 240 с.
4. Лурье Л.Н. Основы высшей математики: Учеб пособие. – М.: Изательско-торг. корпорация «Дашков и Ка». – 2002. -520 с.
5. Мышкис А.Д. Математика для технических вузов: Спец. Курсы. – СПб.: изд-во «Лань». – 2009. – 640 с.: ил.
6. Письменный Д.Т. Конспект лекций по теории вероятностей, математической статистике и случайным процессам. – 4-е изд., испр. – М.: Айрис-пресс, 2002. – 288 с.
7. Свешников А.А. Теория функций комплексной переменной: Учеб. пособие для втузов. – М.: ФИЗМАТЛИТ, 2001. – 336 с.
Содержание
Предисловие . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 3
Общие рекомендации студенту-заочнику по работе
над курсом математики. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .4
Содержание курса «Математика» I семестр. . . . . . . . . . . . . . . . . . .7
Контрольная работа № 1. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .9
Задания к контрольной работе № 1. . . . . . . . . . . . . . . . . . . . . . . . . 18
Контрольная работа № 2. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .25
Задания к контрольной работе № 2. . . . . . . . . . . . . . . . . . . . . . . . . 34
Контрольная работа № 3. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .50
Задания к контрольной работе № 3. . . . . . . . . . . . . . . . . . . . . . . . . 57
Содержание курса «Математика» II семестр . . . . . . . . . . . . . . . . .62
Контрольная работа № 4. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .66
Задания к контрольной работе № 4. . . . . . . . . . . . . . . . . . . . . . . . . 69
Контрольная работа № 5. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .75
Задания к контрольной работе № 5. . . . . . . . . . . . . . . . . . . . . . . . . 79
Контрольная работа № 6. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .87
Задания к контрольной работе № 6. . . . . . . . . . . . . . . . . . . . . . . . . 94
Содержание курса «Математика» III семестр. . . . . . . . . . . . . . . .102
Контрольная работа № 7. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 106
Задания к контрольной работе № 7. . . . . . . . . . . . . . . . . . . . . . . . 111
Контрольная работа № 8. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .120
Задания к контрольной работе № 8. . . . . . . . . . . . . . . . . . . . . . . . 124
Содержание курса «Математика» IV семестр. . . . . . . . . . . . . . . .130
Контрольная работа № 9. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .132
Задания к контрольной работе № 9. . . . . . . . . . . . . . . . . . . . . . . . 140
Контрольная работа № 10. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .154
Задания к контрольной работе № 10. . . . . . . . . . . . . . . . . . . . . . . 165
Список литературы. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 174
