Если , то трубопровод считается гидравлически длинным, в противном случае – гидравлически коротким.

Рисунок 3.1. Схема короткого трубопровода

3.1 Расчет потерь напора на трение

Потери на трение на участках , м. определяются по формуле Дарси-Вейсбаха:

, (3.1)

где 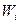- скорость жидкости на участке, м/с;

- диаметр участка, м;

- длина участка, м.

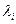- коэффициент гидравлического трения, который зависит от числа Re и от безразмерной величины, характеризующей пограничную геометрию трубы.

Под пограничной геометрией следует понимать не только форму живого сечения, но и геометрические характеристики

поверхности трубы – относительную шероховатость или относительную гладкость , где - средняя высота выступа шероховатости. Абсолютная шероховатость различных трубопроводов приведена в Приложении.

Зависимость впервые была установлена в опытах Никурадзе и Зегджи, выполненных для плотной, однородной, равномерной шероховатости из песка, формированной на поверхности круглых труб. При этом были выведены четыре характерные области зависимости от Re и :

1. Область ламинарного течения ( ). В этом случае справедлива формула Пуазейля

; (3.2)

2. Область гладкостенного режима течения и область гидравлически гладких труб ( ). В этой области вязкий подслой, в котором течение практически можно считать ламинарным, полностью закрывает выступы шероховатости стенки и движение турбулентного ядра потока происходит как бы в гладкой трубе. Для коэффициента гидравлического трения справедлива формула Блазиуса:

; (3.3)

Здесь коэффициент зависит только от Re, однако граница области для каждой данной трубы зависит от ;

3. Область доквадратичного сопротивления . Коэффициент рассчитывается по формуле Альтшуля:

; (3.4)

4. Область квадратичного сопротивления . Коэффициент рассчитывается по зависимости Прандтля-Никурадзе:

. (3.5)

Скорость жидкости W_i, м/с. на участке определим из уравнения неразрывности:

, (3.6)

где - плотность жидкости;

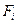- площадь сечения трубы на участке, м²;

- массовый расход жидкости, кг/с.

Площадь сечения трубы F_i, м² на участке определит по формуле:

(3.7)

Чтобы определить коэффициент Дарси необходимо выяснить, какой реализуется режим течения на данном участке. Найдем число Рейнольдса Re, по формуле:

, (3.8)

где кинетический коэффициент вязкости, м²/с.

Суммарные потери напора H_∑, м. на трение составят:

(3.9)

3.2 Определение потерь напора на местных сопротивлениях

Потери напора , м. на местном сопротивлении находим по формуле Вейсбаха:

(3.10)

где - коэффициент потерь на местном сопротивлении. Рассчитывается для данного местного сопротивления (см. Приложение 4).

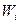- скорость потока на местном сопротивлении, м/с. Рассчитывается из уравнения неразрывности по входному или выходному сечению местного сопротивления в зависимости от типа местного сопротивления
(Приложение 4).

(3.11)

где 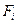- площадь входного или выходного сечения местного сопротивления.

Более подробную информацию о Коэффитциентах местного сопротивления можно найти в учебном пособии: Фалеев В.В., Дроздов И.Г., Фалеев С.В. Гидравлические расчеты в теплоэнергетических системах: Учебное пособие. Воронеж: Издательство ВГТУ, 2000.

Суммарные потери напора H_M∑ , м. на местных сопротивлениях

(3.12)

3.3. Начальные участки труб

На входе в трубу или канал образуется динамический пограничный слой, толщина которого на входном сечении равна нулю, а затем по мере удаления от входного сечения постепенно нарастает. На некотором расстоянии от входного сечения динамический пограничный слой увеличивается настолько, что он заполняет все сечение трубы (канала). Если процесс течения рабочей среды является изотермическим, то профиль скорости в сечении трубы или канала, после того как динамические пограничные слои сомкнулись, практически не изменяется и остается постоянным (рис.3.2). Расстояние , на котором происходит смыкание динамических пограничных слоев, называется длиной начального участка (длиной динамической стабилизации потока).

	Пограничный слой

Рисунок 3.2

Стабилизация течения при возникновении турбулентности на входной кромке трубы наступает на расстоянии

( ) (3.13)

Если же организован плавный вход, то развивается ламинарный пограничный слой и в диапазоне чисел Рейнольдса можно использовать соотношение

. (3.14)

Формулы (3.13) и (3.14) справедливы при использовании течений жидкости и газа на начальном участке.

Для вполне шероховатых круглых труб справедлива формула Г.В.Филиппова

, (3.15)

где - коэффициент гидравлического трения для стабилизированного течения в трубе.

Эта формула справедлива для гидравлических гладких труб и в переходной области турбулентного режима.

Коэффициент гидравлического трения начального участка трубы (канала) больше, чем той части трубы (канала), где течение стабилизировалось.

Для ламинарного изотермического течения

. (3.16)

При турбулентном течении на начальном участке прямой трубы

. (3.17)

На начальном участке

, (3.18)

где определяется по формуле (3.13).

3.4 Суммарные потери напора в трубопроводе

Суммарные потери напора H_∑, м. в трубопроводе складываются из потерь на трение и местных сопротивлениях

(3.19)

Если , то трубопровод считается гидравлически длинным, в противном случае – гидравлически коротким.