Решение систем линейных алгебраических уравнений методом Гаусса. Две системы называются эквивалентными (равносильными), если их множества решений совпадают, т.е

Две системы называются эквивалентными (равносильными), если их множества решений совпадают, т.е. решения каждой из них является решением другой, или если обе системы несовместны.

Элементарные преобразования системы уравнений:

1) перестановка местами уравнений;

2) умножение (деление) обеих частей уравнения на число, отличное от нуля;

3) умножение (деление) любого уравнения на число (не равное нулю) и прибавление затем его к другому уравнению;

4) исключение из системы уравнений вида ;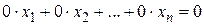

Все элементарные преобразования обратимы и линейная система, полученная при элементарном преобразовании, эквивалентна исходной. На этом основан метод решения системы, называемый методом исключениянеизвестныхили методом Гаусса. Он заключается в том, что на первом шаге исключается, скажем, переменная 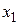из всех уравнений, кроме одного (обычно первого), затем 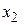из остальных уравнений кроме одного (обычно второго) и т.д. (прямой ход). Этот процесс закончится тем, что либо одна из переменных получит вполне определенное значение, либо ее можно выразить через оставшиеся переменные, которые называются свободными переменными. Свободным переменным могут принимать произвольные значения. Затем обратным ходом вычисляются в обратном порядке значения всех переменных, называемых базисными. Если при прямом ходе возникнет равенство 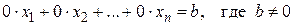, то система несовместна.

Пример. Решить методом Гаусса систему

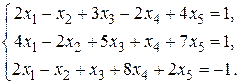
◄ Так как элементарные преобразования затрагивают только коэффициенты системы и свободные члены, то будем преобразовывать лишь строки расширенной матрицы системы:

.

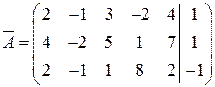Вычитая из второй строчки первую, умноженную на 2, и из третьей первую, получим

.

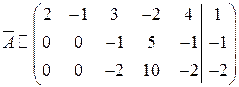Умножив (виртуально) вторую строчку на (- 2) и затем прибавив ее к третьей, а также умножив вторую строчку на (- 1) будем иметь:

.

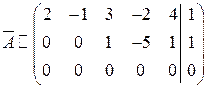Убираем из системы последнюю строку и переставляем местами второй и третий столбец (вместе с обозначениями неизвестных, при которых эти столбцы коэффициентов находятся):

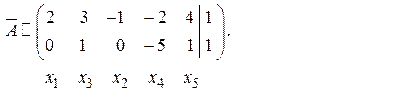
Переносим направо за вертикальную черту (за знаки равенств) третий, четвертый и пятый столбец с соответствующими обозначениями неизвестных (меняя знаки коэффициентов на противоположные):

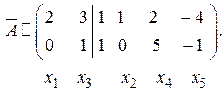
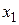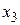Прямой ход закончен. Базисными переменными в решении будут и , а свободным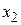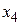и , и .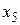

Начинаем обратный ход. Умножаем последнюю строчку на (- 3) и прибавляем к первой:

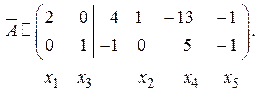
Поделив первую строчку на 2, получаем окончательно:

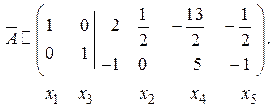
Слева от вертикальной линии в результате реализации прямого и обратного хода метода Гаусса получена единичная матрица. Записываем общее решение системы:

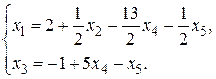
Вводя для свободных переменных обозначения 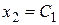, , 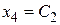, 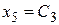общее решение запишем в виде:

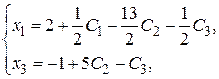
где 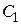. 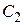, 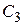- любые числа.

Частное решение системы получают при придании конкретных значений свободным переменным. Положим, например, в данном случае 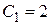, , 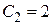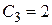. Тогда будем иметь следующее частное решение: , , , , . ►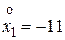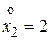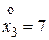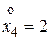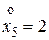