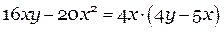Вынесение общего множителя за скобки

Одночлен

Одночлен – число, переменная («буква»), степень или комбинация из них, составленные с помощью умножения, взятая со знаком.

Сначала пишут численную часть – коэффициент, а потом буквенную. Буквы ставят в алфавитном порядке.

Примеры:

Одночлен – число: 3; 0; -1,2….

Одночлен – переменная: a; x; f …

Одночлен – степень: x³; a²; …

Одночлен – комбинация: 2,4а⁵bc²; -3xy²

Если у одночленов совпадает буквенная часть, то они называются подобными.

Для сложения/вычитания подобных одночленов надо:

1) сложить/вычесть коэффициенты (это числа в составе одночленов);

2) буквенную часть оставить без изменений.

Примеры:

3а + 5а = (3+5)а = 8а

-7a²b – 9a²b = (-7 - 9)a²b = -16а²b

Для умножения/деления одночлена на одночлен надо:

1) определить знак результата;

2) выполнить действия над численной частью одночленов;

3) выполнить действия над буквенной частью одночленов.

Примеры:

Многочлен

Многочлен – выражение, составленное из неподобных одночленов с помощью сложения и вычитания.

Примеры:

-3а² + 7с; -12 – 4,5а

Сложение/вычитание многочленов сводится к приведению подобных одночленов, из которых состоят эти многочлены.

Примеры:

Для умножения многочлена на многочлен надо перемножить все «элементы» одного многочлена (т.е. все одночлены) на все «элементы» другого многочлена и соединять их знаком сложения. Это еще называют «фонтанчиком».

Примеры:

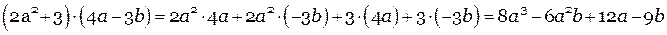
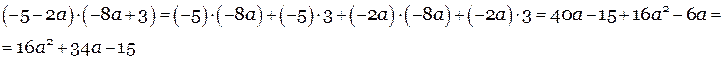
Формулы сокращенного умножения

(ФСУ)

Разность квадратов

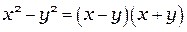
Правую часть этой формулы желательно начинать писать со скобки со знаком минус, потому что именно она задает порядок вычитания в «свернутом» виде.

Квадрат суммы/разности

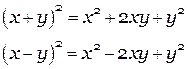
Сумма/разность кубов

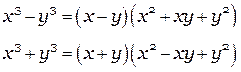
Куб суммы/разности

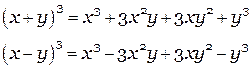
Все формулы сокращенного умножения действуют в обе стороны. «x» и «y» в формулах следует понимать не как только переменные «буквы», но как обозначения «контейнеров» для выражений. Объясню на таком воображаемом примере.

Представим, что «x» и «y» - машины, которые едут в пробке. В них может сидеть кто угодно, и, что бы ни произошло с самими машинами, это происходит с ними целиком и полностью, т.е. и с их пассажирами.

( a + c )²= a ²+2 a c + c ²

Способы разложения многочленов

На множители

В рамках знаний 7го класса есть только два способа разложить многочлен на множители:

1) Использовать формулы сокращенного умножения;

2) Выносить за скобки общий множитель.

Вынесение общего множителя за скобки

Чтобы вынести общий множитель за скобки нужно:

1) Мысленно увидеть каждое из слагаемых, из которых состоит наше выражение;

2) Увидеть, входящие в эти слагаемые, сомножители;

3) Определить, есть ли общие сомножители у КАЖДОГОиз слагаемых;

4) Вынести это общее, написав его перед скобками;

5) В скобках определить оставшуюся часть делением каждого из слагаемых на вынесенное общее.

Примеры:

Разложить на множители многочлен: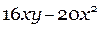

Рассмотрим это задание по пунктам. Все эти этапы необязательно записывать, но продумывать в голове их нужно обязательно!

1) Слагаемые: 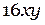и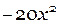

2) Первое слагаемое состоит из сомножителей: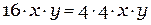

Второе слагаемое состоит из сомножителей:

3) Общий сомножитель:

4) и 5)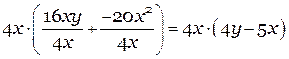

В тетради же достаточно простой и краткой записи: