Ш. А. Алимов, Ю.М. Колягин и другие «Алгебра и начала математического анализа 10-11 классы»
В этой книге [2] учебник и задачник не разделены, задачи идут после параграфа, а так же в конце главы есть закрепляющие упражнения.
В данной учебной литературе исследованию функции уделена целая глава, она так и называется «Применение производной к исследованию функций». Предполагается, что учащиеся уже знакомы с производной, и только при этом условии можно продолжать обучение.
Глава состоит из 5 параграфов: возрастание и убывание функции, экстремумы функций, применение производной к построению графиков функций, наибольшие и наименьшее значение функции, выпуклости графика функции.
В первом параграфе главы автор знакомит учеников с возрастанием и убыванием функции. Рассмотрев 2 примера, делается вывод, что производная функции больше (меньше) нуля, то функция возрастает (убывает) на некотором промежутке. Далее идет знакомство с теоремой Лагранжа, но без доказательства, а также следствие теоремы.
Во втором параграфе главы речь идет об экстремумах функции. Учащимся даются определения точек максимума, минимума, экстремума, стационарных, а также теорема Ферма.
В следующем параграфе главы показывается как строить график функции с помощью производной. Способ подачи материала в данном параграфе основан на задачах-примерах. Разобрав 1 задачу, авторы дают читателю свой алгоритм исследования функции для построения графика. По их алгоритму нужно найти:
1. Область определения функции
2. Производную функции
3. Стационарные точки
4. Промежутки возрастания и убывания функции
5. Точки экстремума и значения функции в этих точках
Учащимся предлагается результаты исследования оформлять в виде таблицы. Так же дается совет, что у четных (нечетных) функций можно построить часть при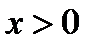 
, а затем отобразить относительно оси ординат.
В четвертом параграфе рассматривается вопрос о наибольшем и наименьшем значении функции. Он разделен на 3 подпункта. В первом подпункте дается алгоритм нахождения наибольшего (наименьшего) значения функции на отрезке. Для нахождения наибольшего (наименьшего) значения функции на отрезке нужно сравнить значения функции в точках максимума (минимума) и на концах отрезка. Во втором подпункте аналогичный вопрос, только вместо отрезка дается интервал. Третий подпункт дается со знаком «*», это значит, что он необязателен для изучения. В нем дается утверждение, что если значения функции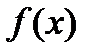 
неотрицательны на некотором промежутке, то эта функция и функция 
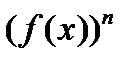, где n – натуральное число, принимают наибольшее (наименьшее) значение в одной и той же точке. Опираясь на данные этого утверждения, в учебнике разбирается несколько задач.
В последнем параграфе рассматривается выпуклость и точки перегиба функции. Этот параграф также обозначен знаком «*», и он тоже состоит из 3 подпунктов. В первом подпункте рассказывается производная второго порядка. Во втором подпункте речь идет о выпуклости функции, даются понятия функции выпуклой вверх, выпуклой вниз. Последний подпункт называется «точки перегиба». Учащимся дается определение точки перегиба: «в точке перегиба дифференцируемая функция меняет направление выпуклости».
Подведя итог по данному учебному пособию, можно сказать, что в нем тема «исследование функции», в отличие от учебника Мордковича, выделена в отдельную главу, также представленный алгоритм исследования функции проще. Среди упражнений для решения часто встречаются междисциплинарные задачи.