Тренажер по математике при подготовке к ОГЭ (задание 5)

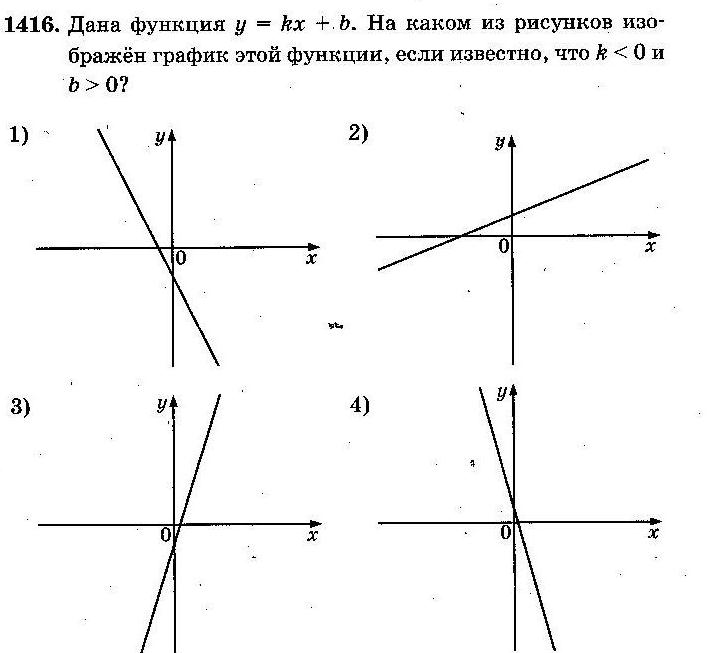
1. y=kx+b – линейная функция. Графиком линейной функции является прямая, пересекающая ось Oy в точке (0;b).

Если k>0, то функция возрастающая,

k<0, то функция убывающая

Если b=0, то y=kx –прямая пропорциональность и график проходит черезначало координат.

Чтобы построить график линейной функции, надо выбрать две точки.

Задание 5 (тип 1)

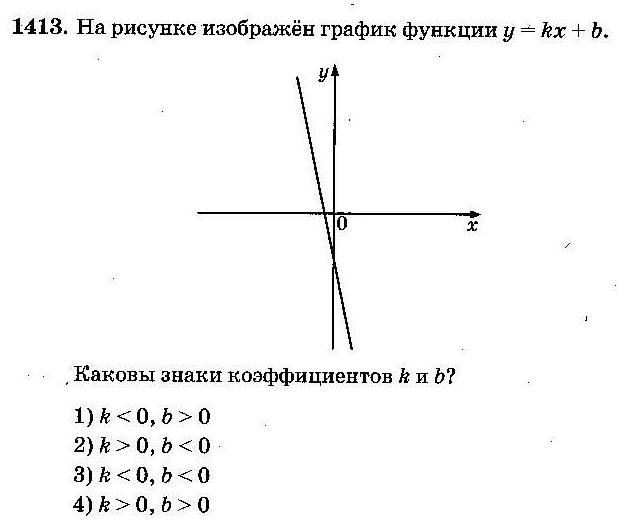
АЛГОРИТМ:

a. Так как на рисунке указан график убывающей функции, то k<0, и ответы № 2 и № 4 не подходят;

b. Прямая пересекает ось Oy ниже оси Ox, поэтому b<0, следовательно, выбираем ответ № 3

Ответ: 3

Реши самостоятельно:

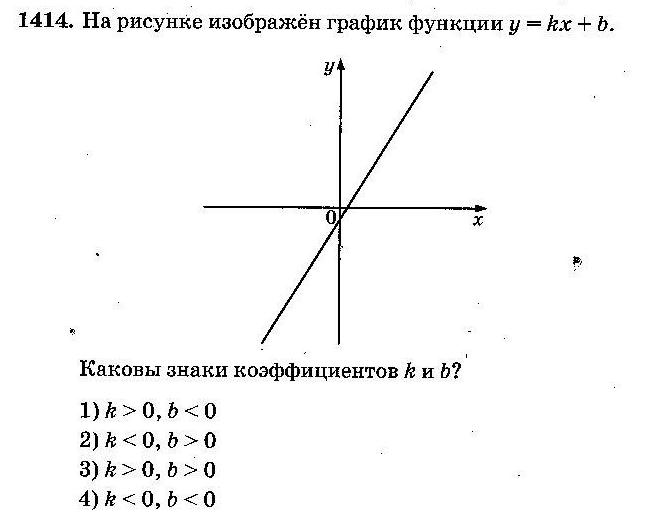
Задание 5 (тип 2)

АЛГОРИТМ:

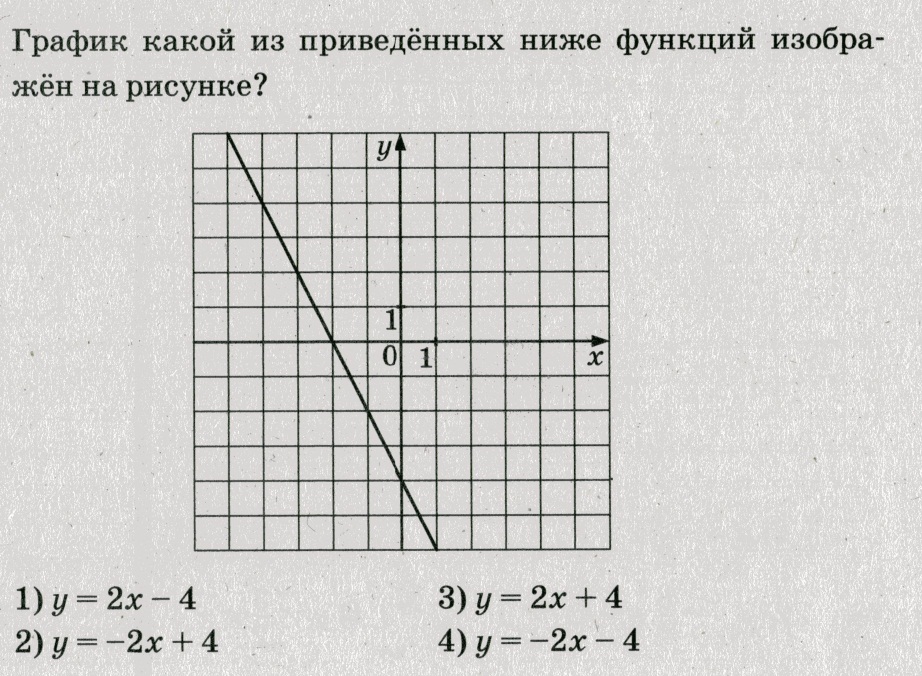
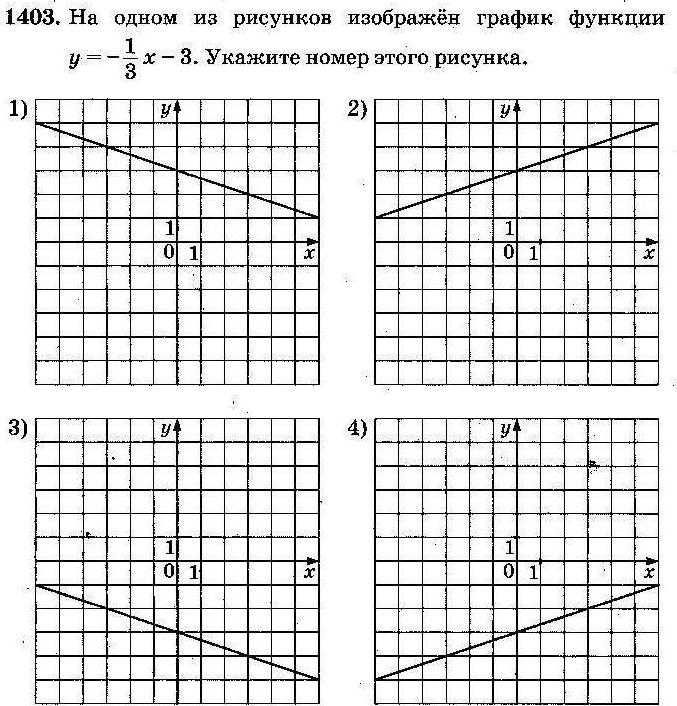
a. Так как на рисунке указан график убывающей функции, то k<0, и ответы 1 и 3 не подходят;

b. Прямая пересекает ось Oy в точке (0;–4), поэтому b= – 4, выбираем ответ 4

Ответ: 4

Реши самостоятельно:

1.

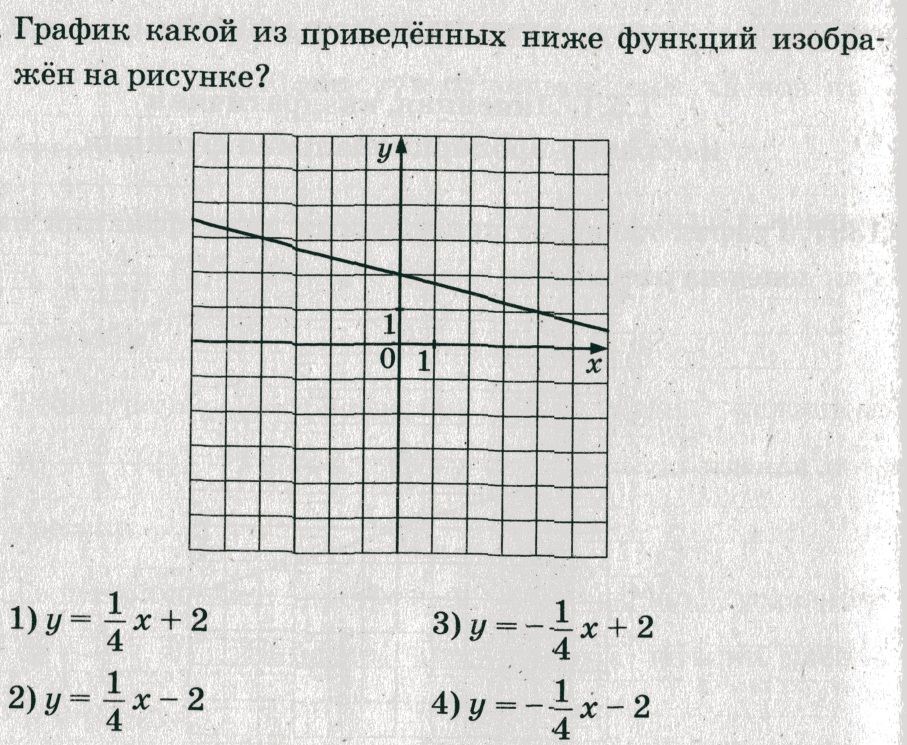
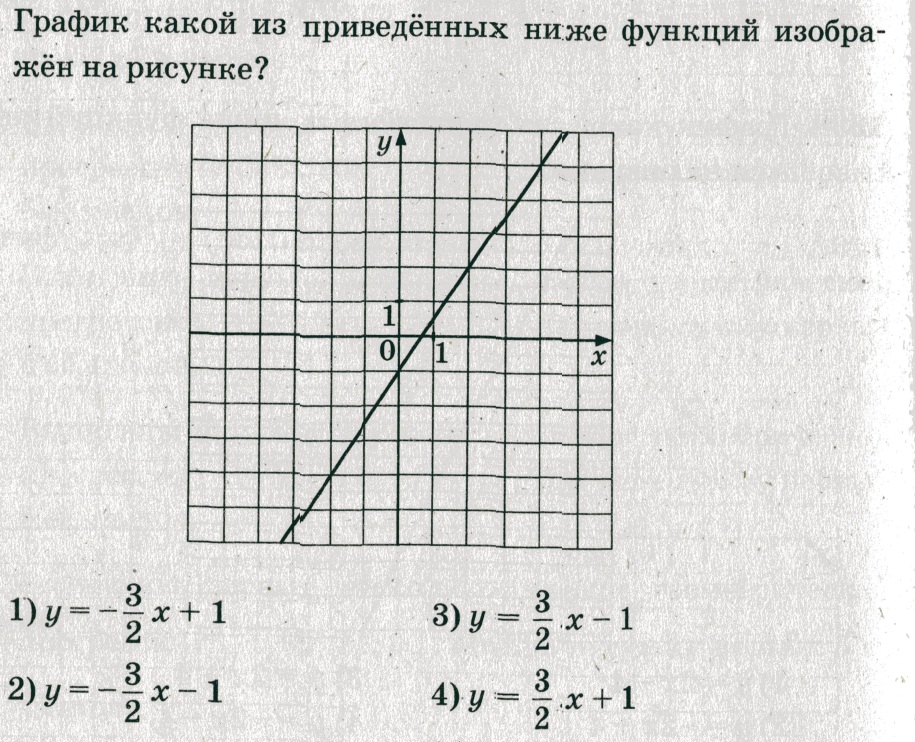
Задание 5 (тип 3)

АЛГОРИТМ:

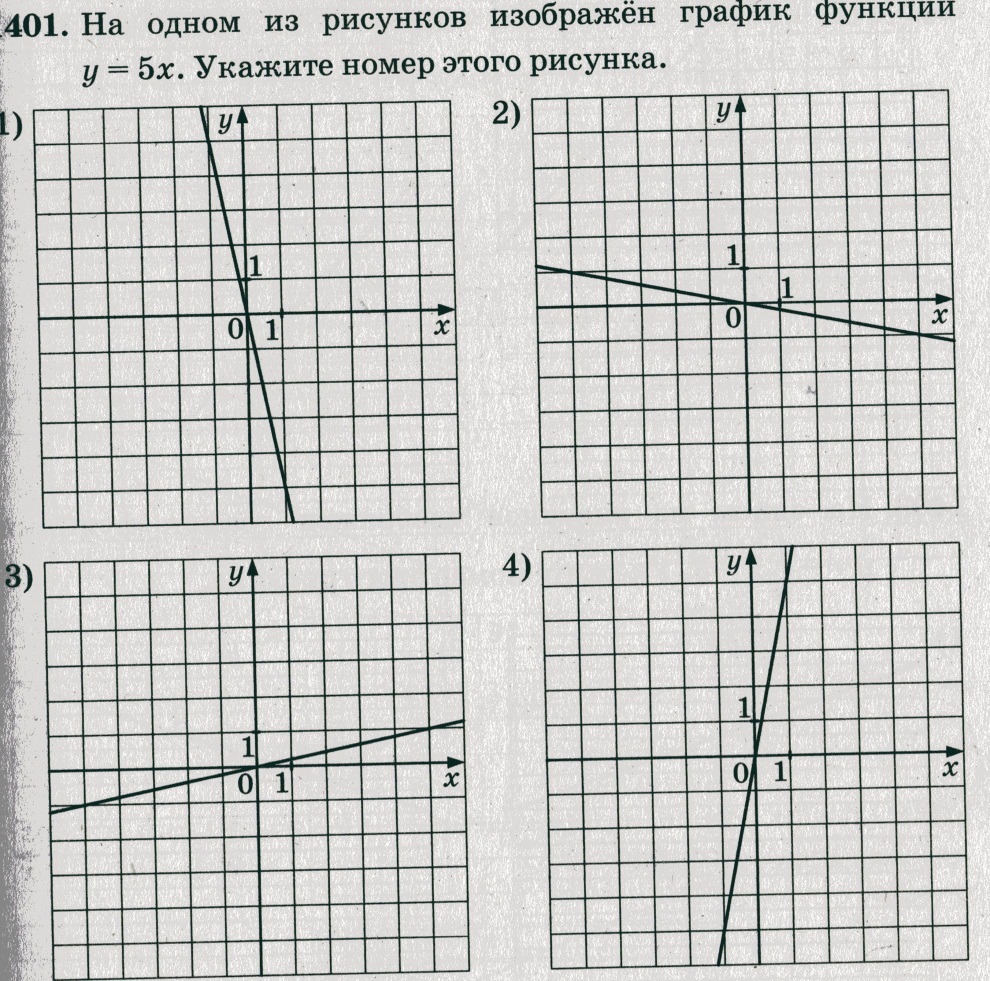
a. Так как в формуле k = 5>0, то изображен график возрастающей функции и ответы № 1 и № 2 не подходят;

b. Выбираем две точки с целыми координатами, принадлежащие графику. Подставим в уравнение y = 5x (см. рис. 3). Точка (5;1): 1=5×5 – неверно, следовательно, рисунок

№ 3 не является графиком функции y = 5x. Проверим рисунок № 4. Точка (1;5) лежит на прямой. Подставим её координаты в уравнение y = 5x: получим 5 = 5×1 – верно, следовательно, рисунок № 4 является графиком функции y = 5x.

Ответ: 4

Реши самостоятельно:

Задание 5 (тип 4)

АЛГОРИТМ:

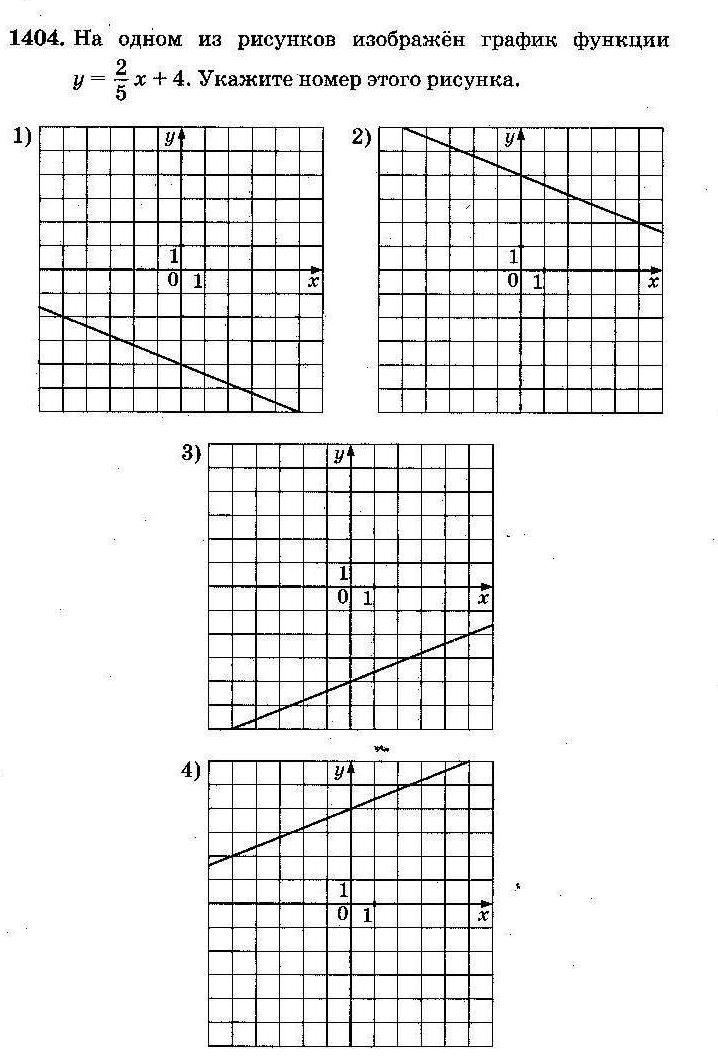
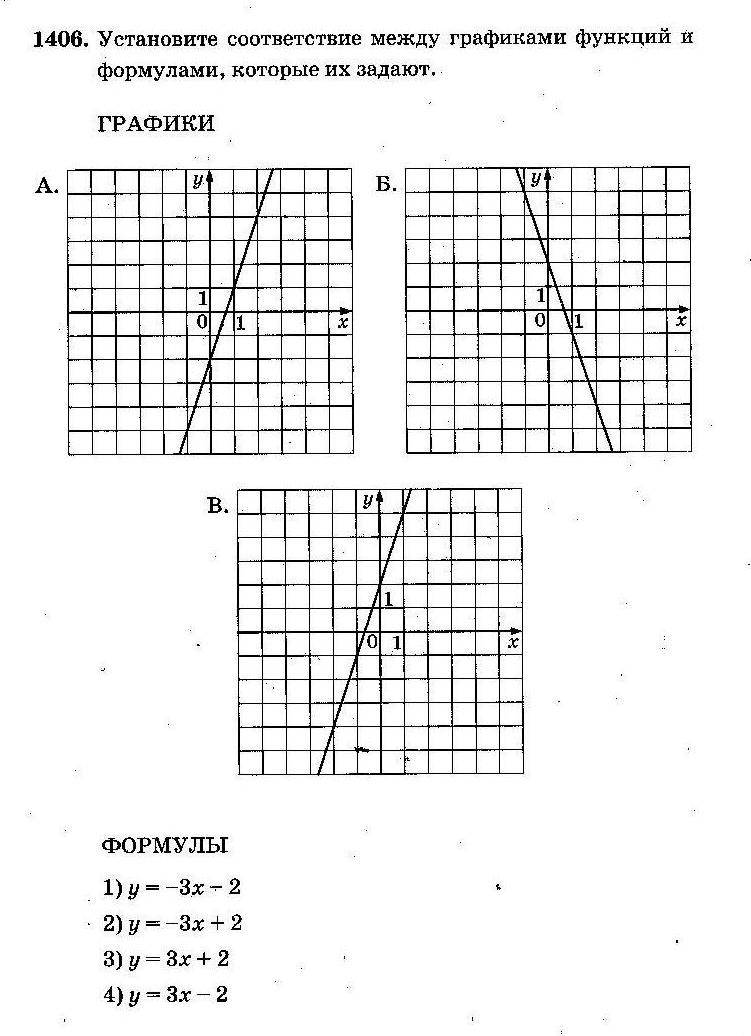
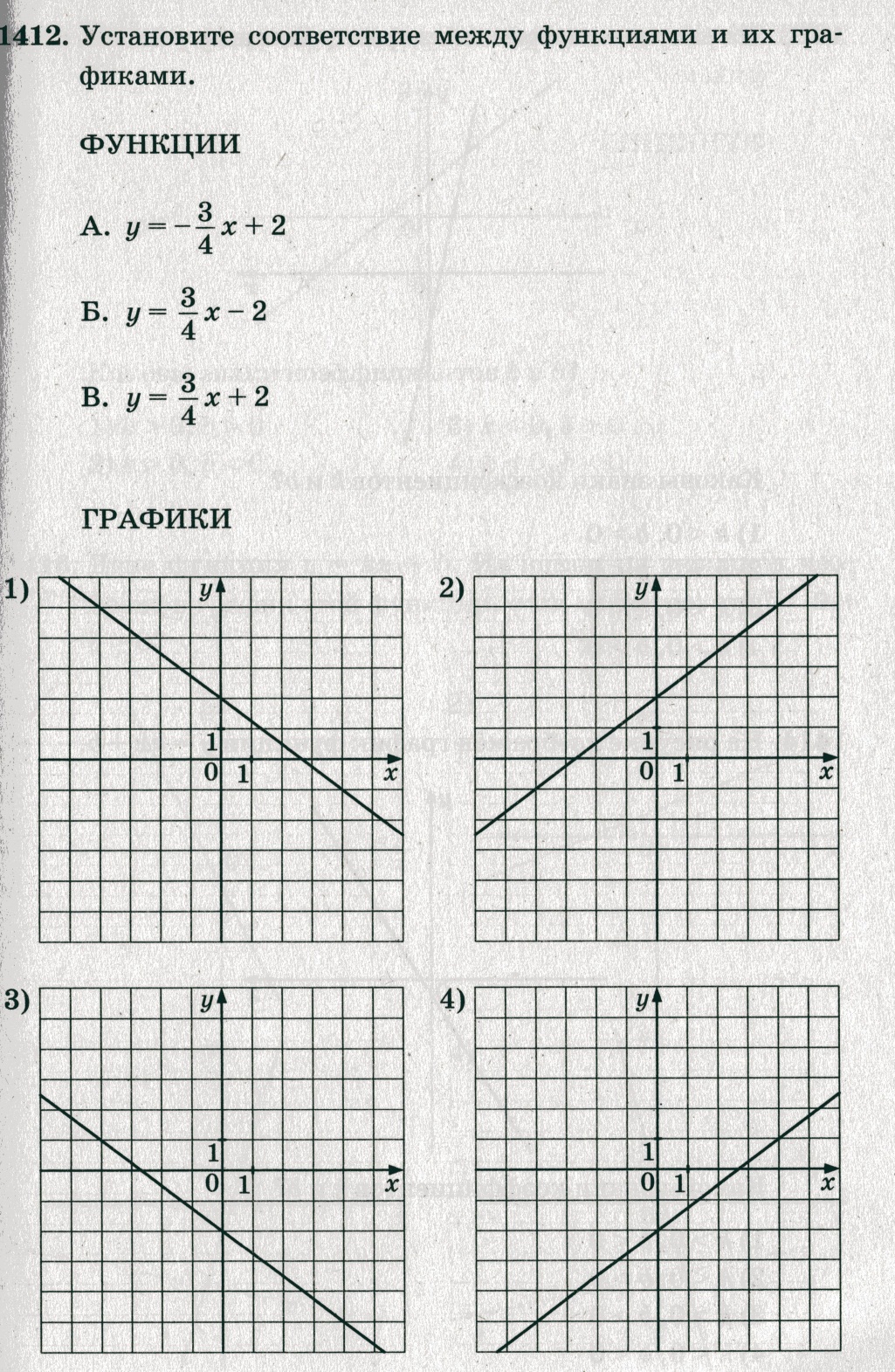
А. Функция возрастает (k>0), следовательно, подходят № 3 и № 4; пересечение графика с осью Oy в точке (0; – 2), следовательно, подходит № 4;

Б. Аналогично, функция убывает (k<0),следовательно, подходят № 1 и № 2, пересечение графика с осью Oy в точке (0; 2), следовательно, подходит № 2;

В. Функция возрастает (k>0), следовательно, подходят № 3 и № 4; пересечение графика с осью Oy в точке (0; 2), следовательно, подходит № 3;

Ответ: А–4; Б–2; В–3

Реши самостоятельно:

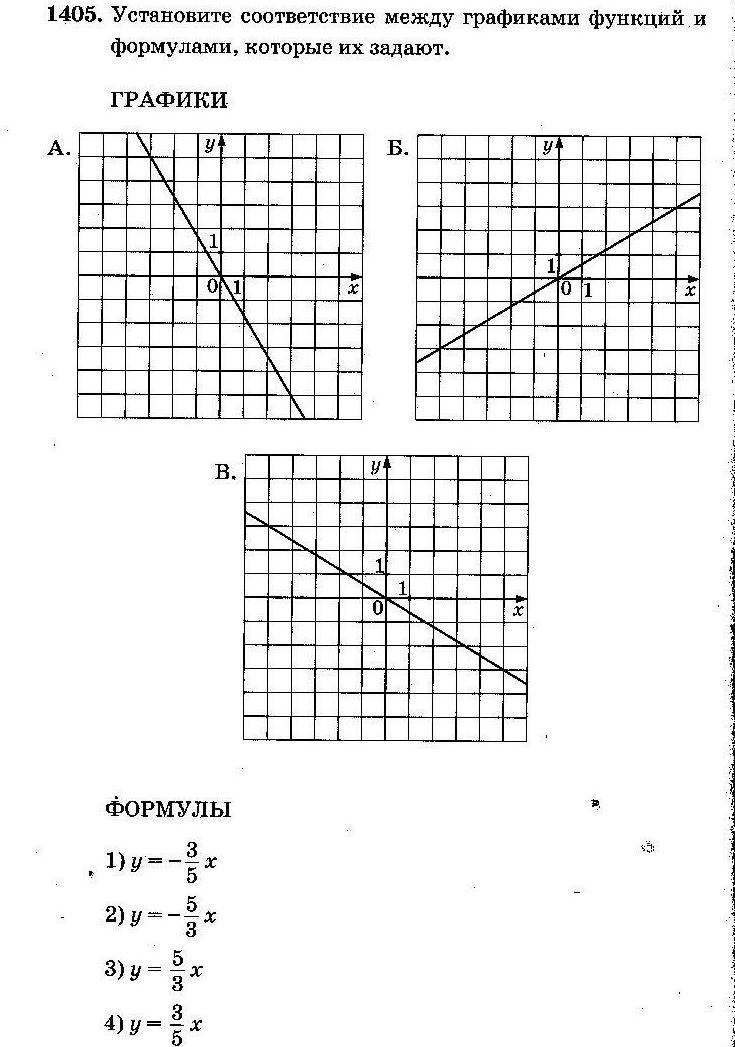
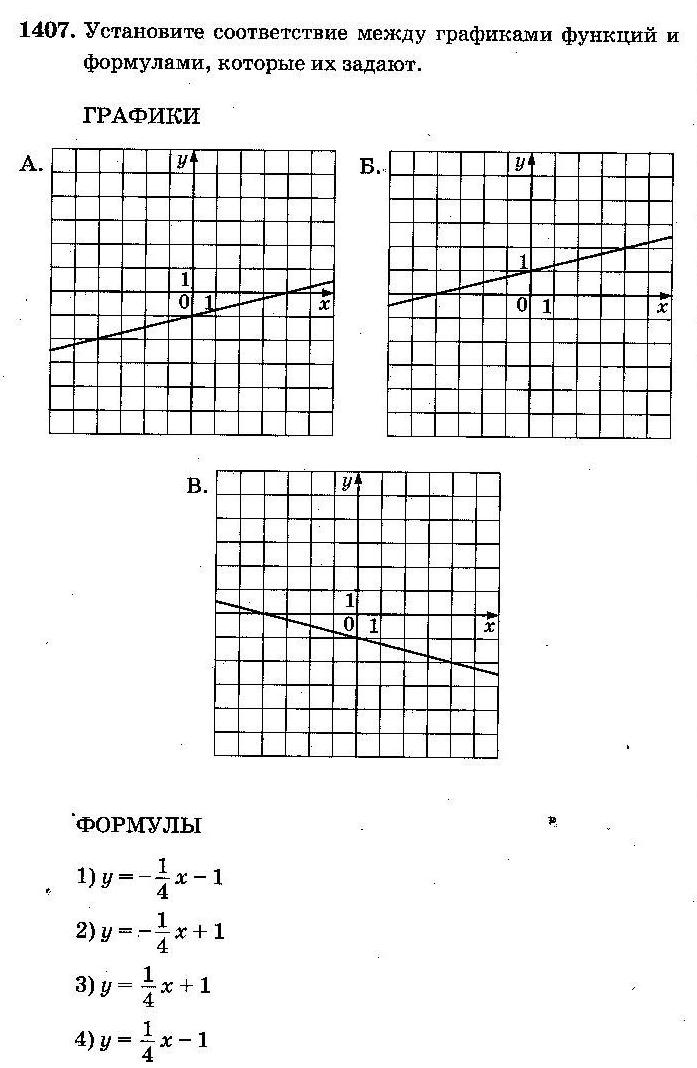
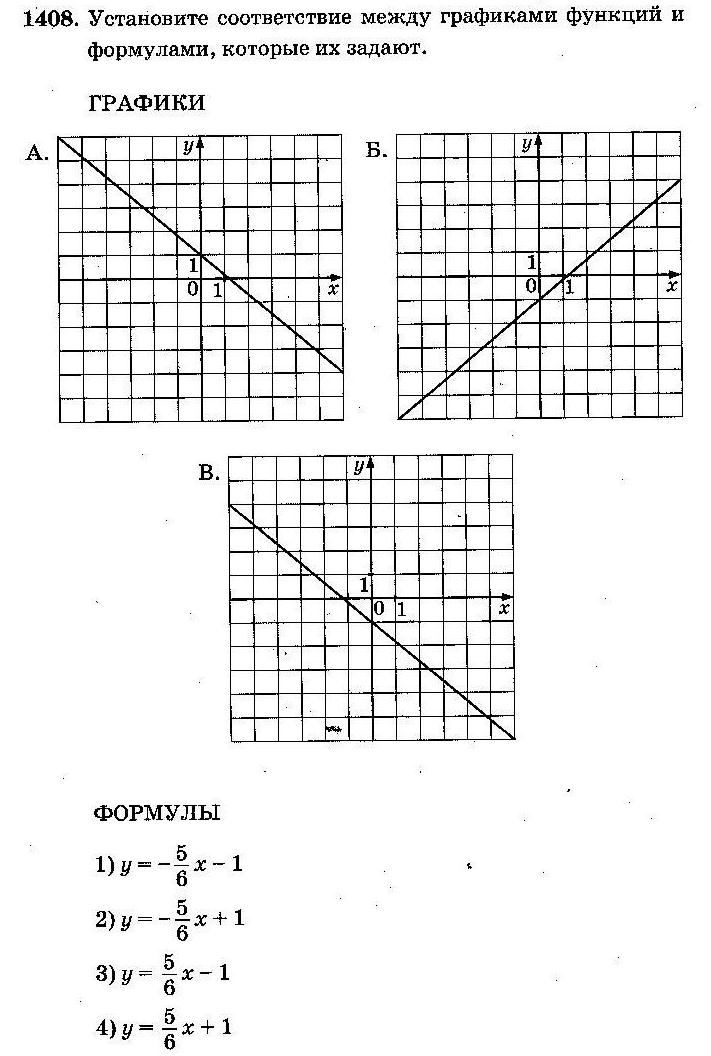
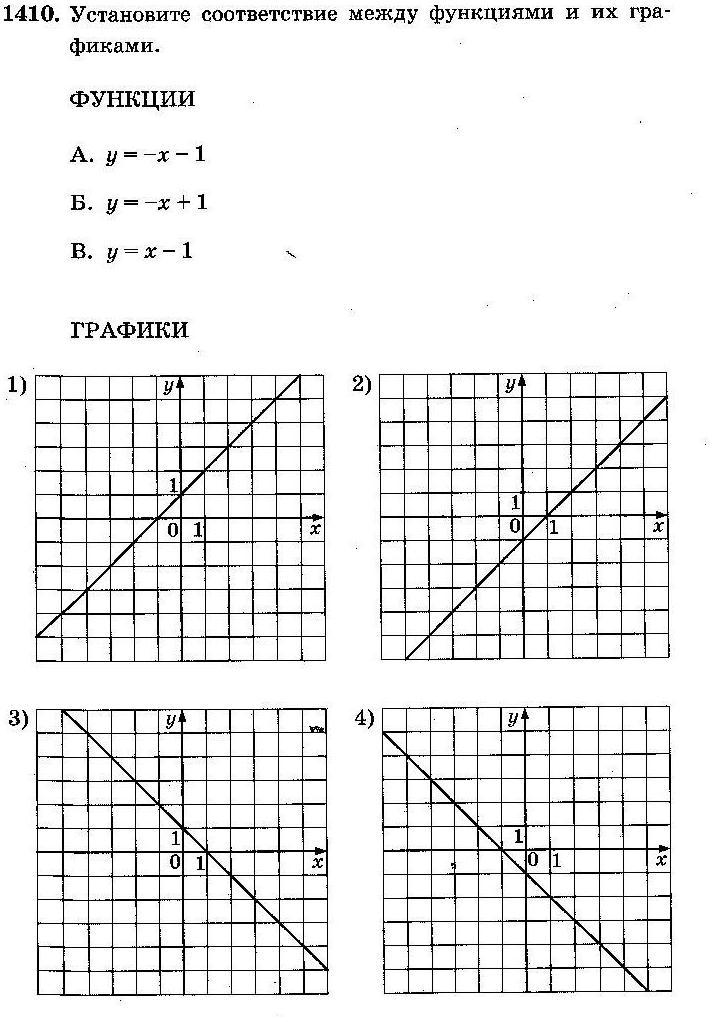
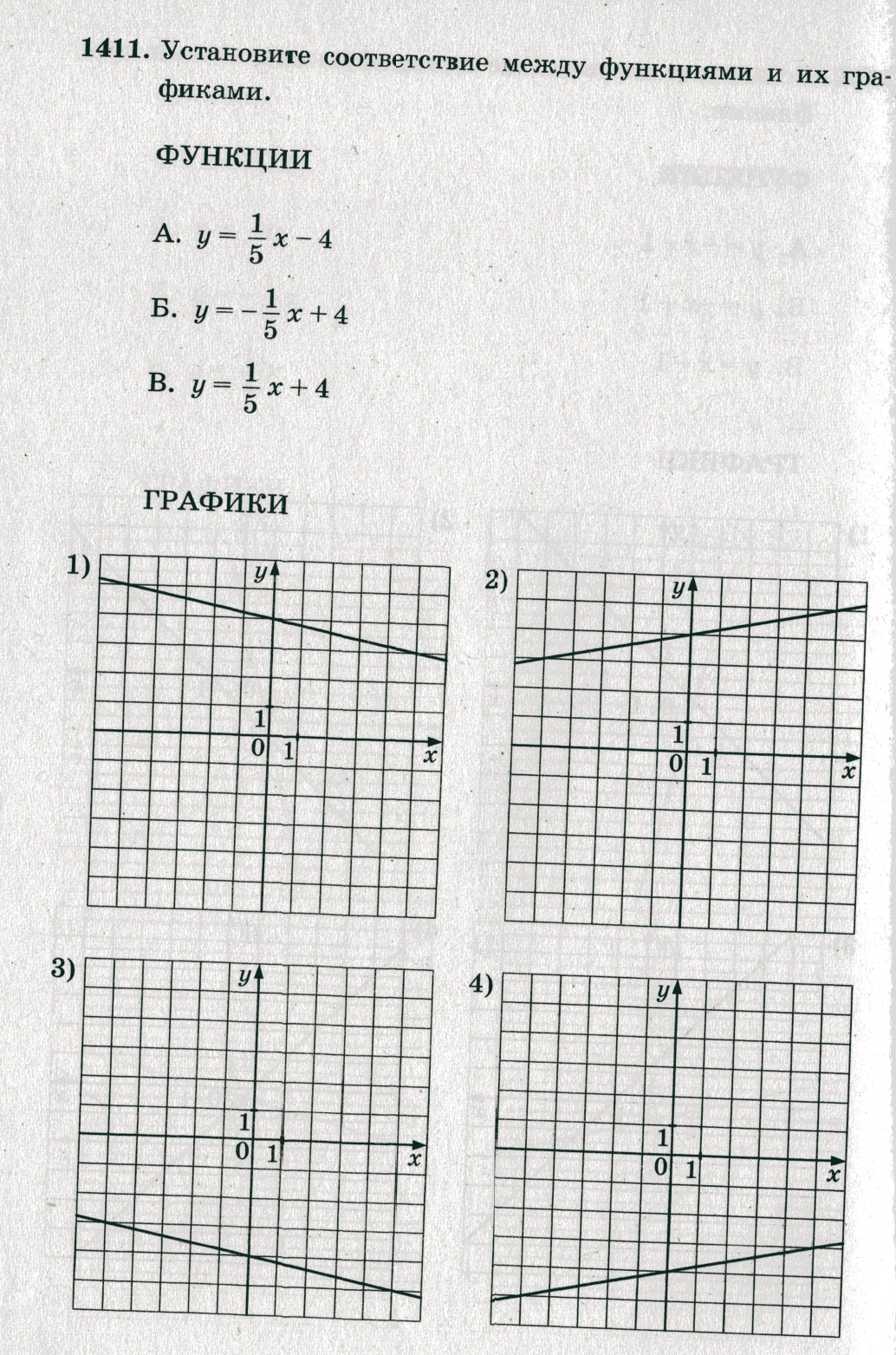
2. y=ax²+bx+c, a≠0 – квадратичная функция. Графиком квадратичной функции является парабола, пересекающая ось Oy в точке (0;c).

Если a>0, то ветви параболы направлены вверх,

a<0, то ветви параболы направлены вниз.

Абсцисса вершины параболывычисляется по формуле:x₀= 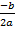, y₀ – подставляем значение x₀ в формулу y₀=ax₀ ²+bx₀ +c

Задание 5 (тип 5)

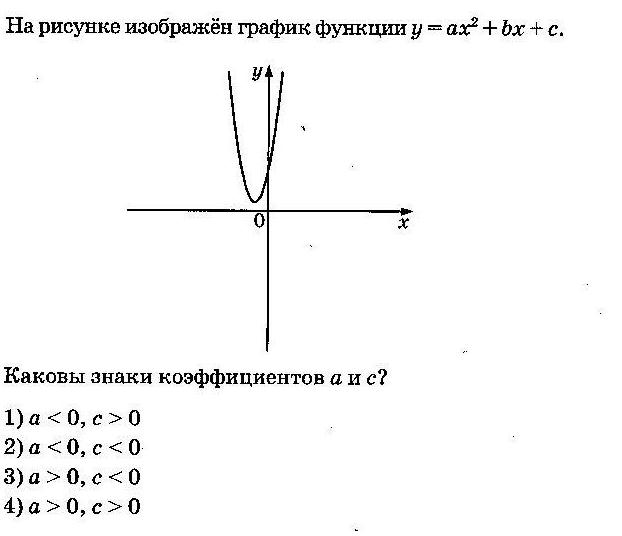
АЛГОРИТМ:

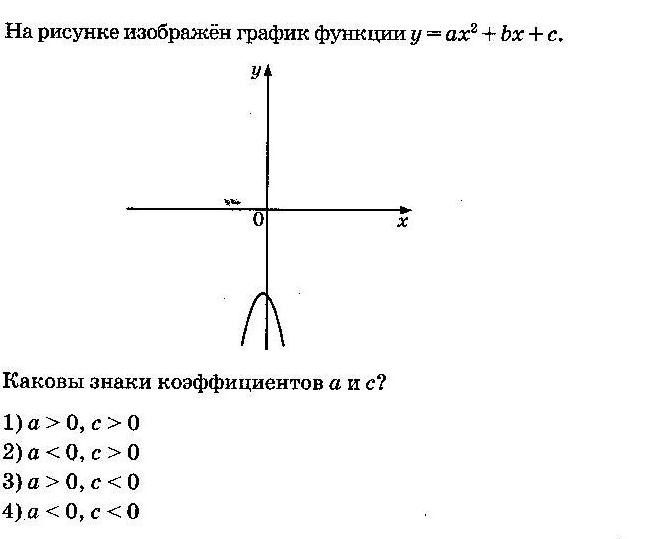
a. Так как на рисунке ветви параболы направлены вверх, то a>0, и ответы № 1 и № 2 не подходят;

b. Парабола пересекает ось Oy в точке, расположенной выше оси Ox, поэтому c>0, следовательно, выбираем ответ № 4

Ответ: 4

Реши самостоятельно:

1.

2.

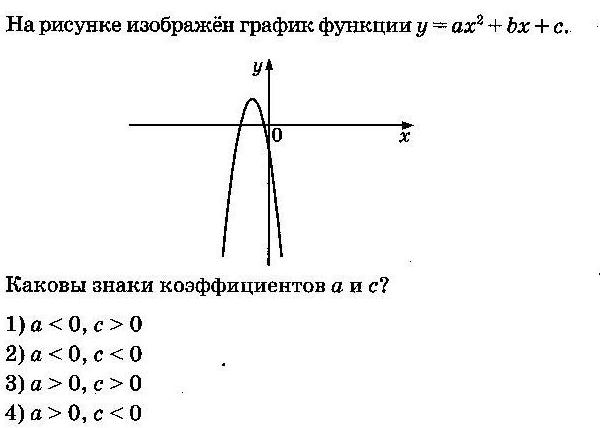
Задание 5 (тип 6)

АЛГОРИТМ:

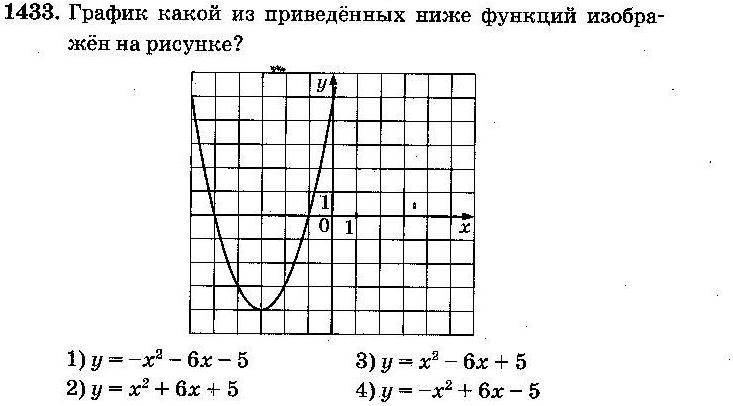
a. Так как на рисунке ветви параболы направлены вверх, то a>0, и ответы № 1 и № 4 не подходят;

b. Парабола пересекает ось Oy в точке (0;5), поэтому c=5, следовательно, подходят ответы № 3 и № 2.

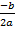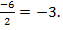c. Вычислим абсциссу вершины параболы№ 2по формуле x₀= : x₀= № 2 подходит. Вычислим абсциссу вершины параболы№ 3по формуле 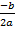x₀= : x₀= 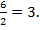– не подходит. Следовательно, выбираем ответ № 2

Ответ: 2

Реши самостоятельно:

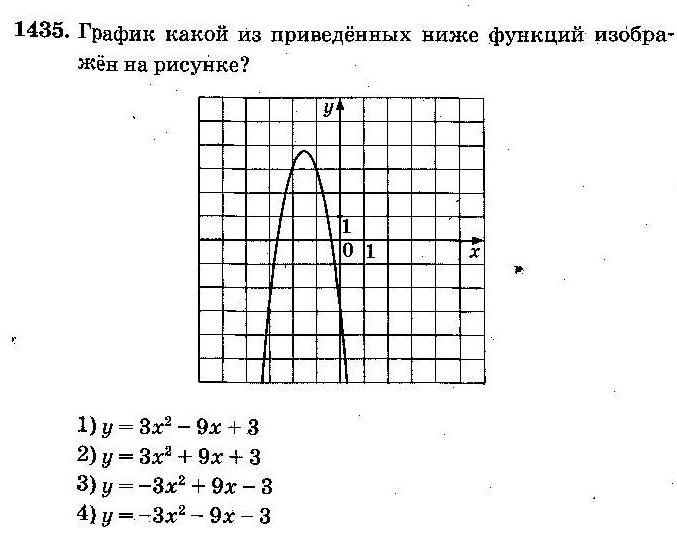
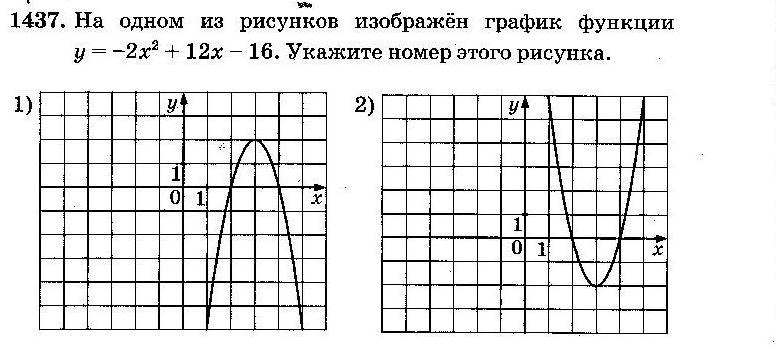
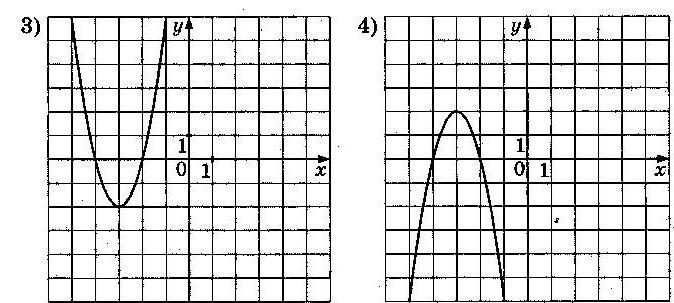
Задание 5 (тип 7)

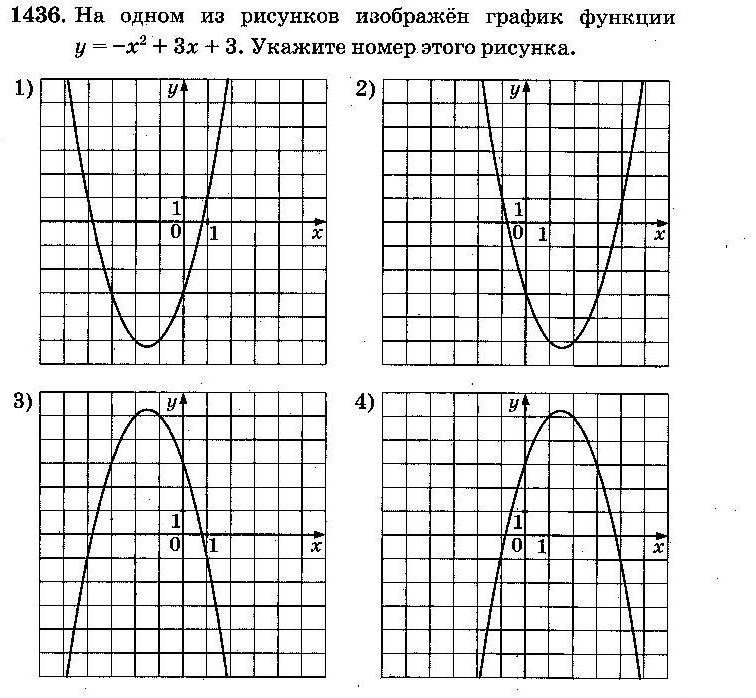
АЛГОРИТМ:

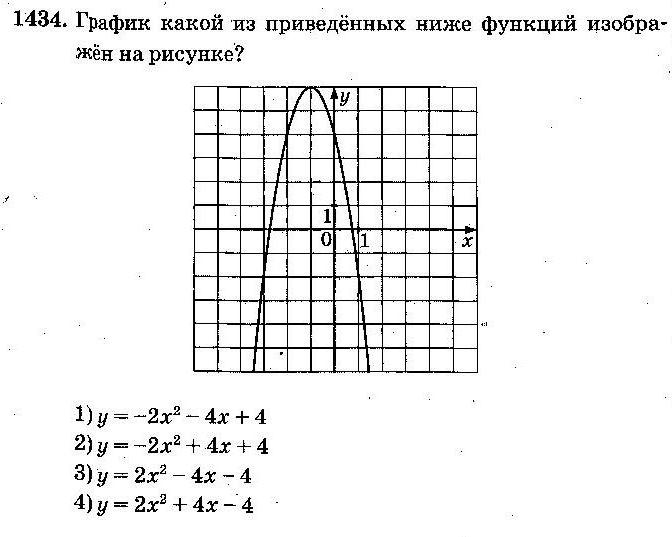
a. Так как в формуле a = –1<0, то ветви параболы направлены вниз, и ответы № 1 и № 2 не подходят;

b. Вычислим абсциссу вершины параболыпо формуле 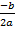x₀= : x₀= 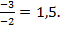Следовательно, выбираем ответ № 4

Ответ: 4

Реши самостоятельно:

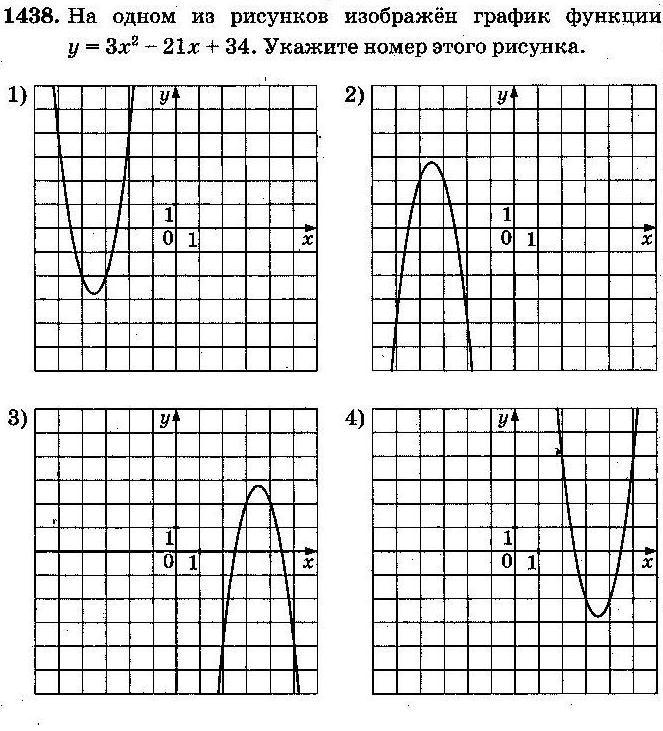
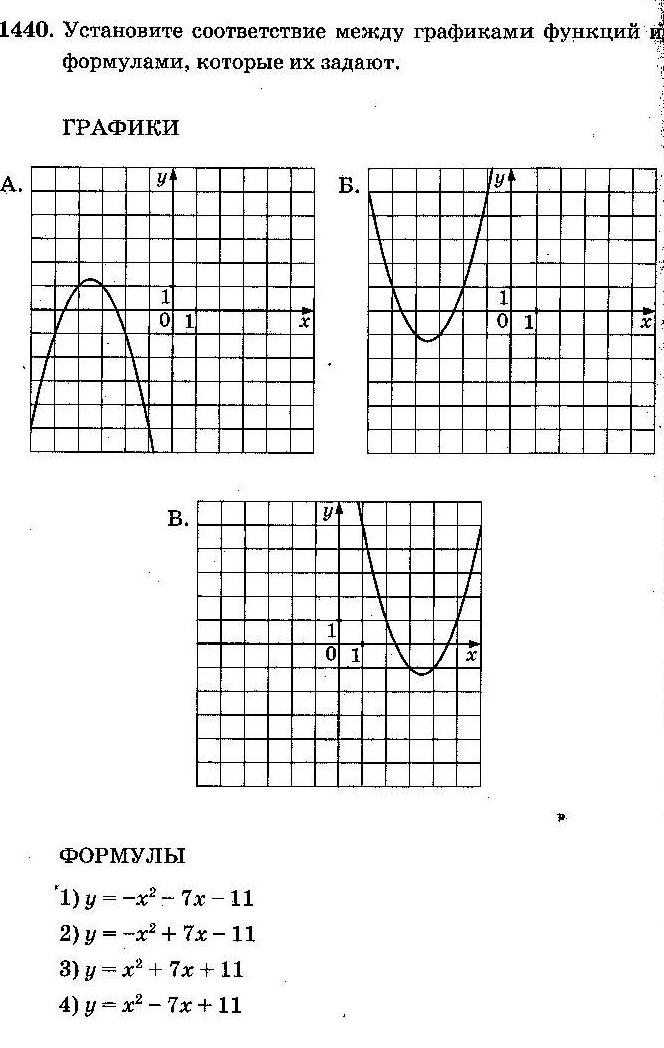
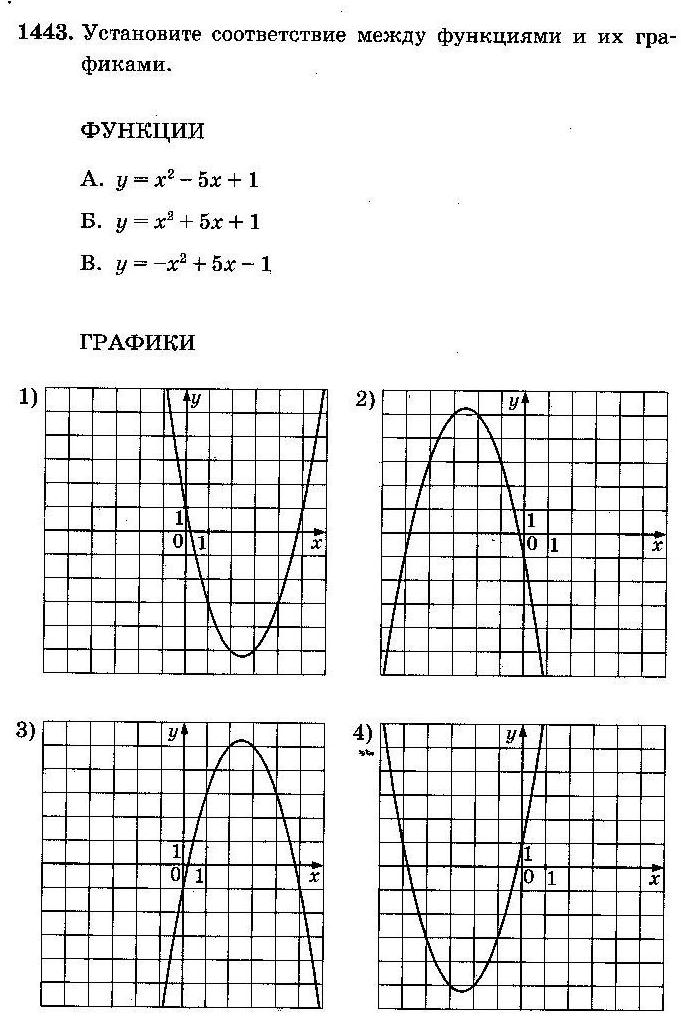
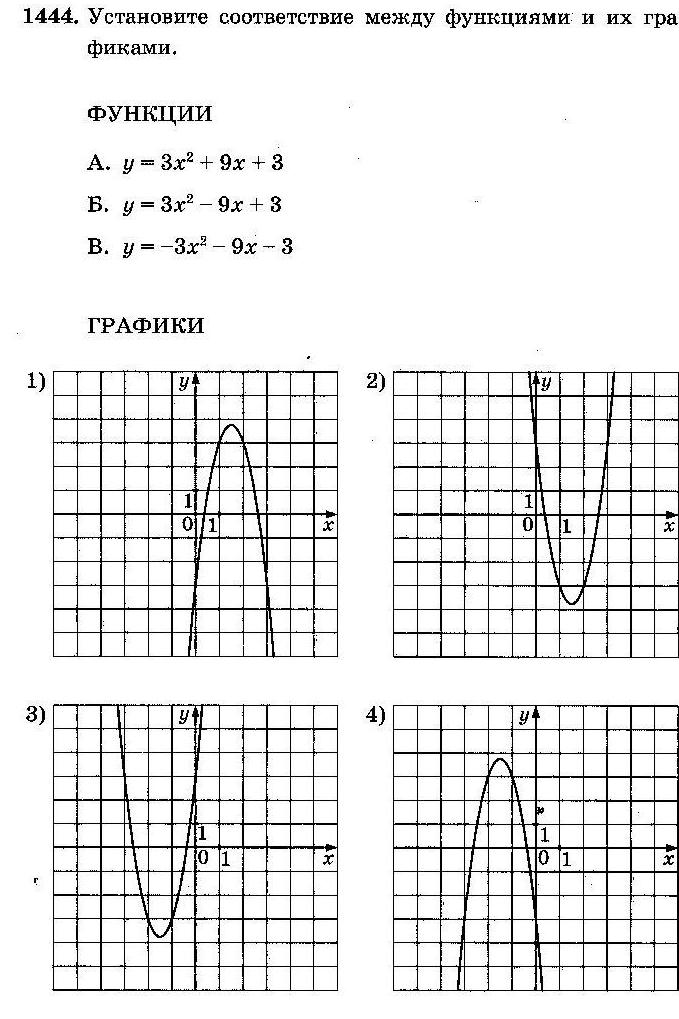
Задание 5 (тип 8)

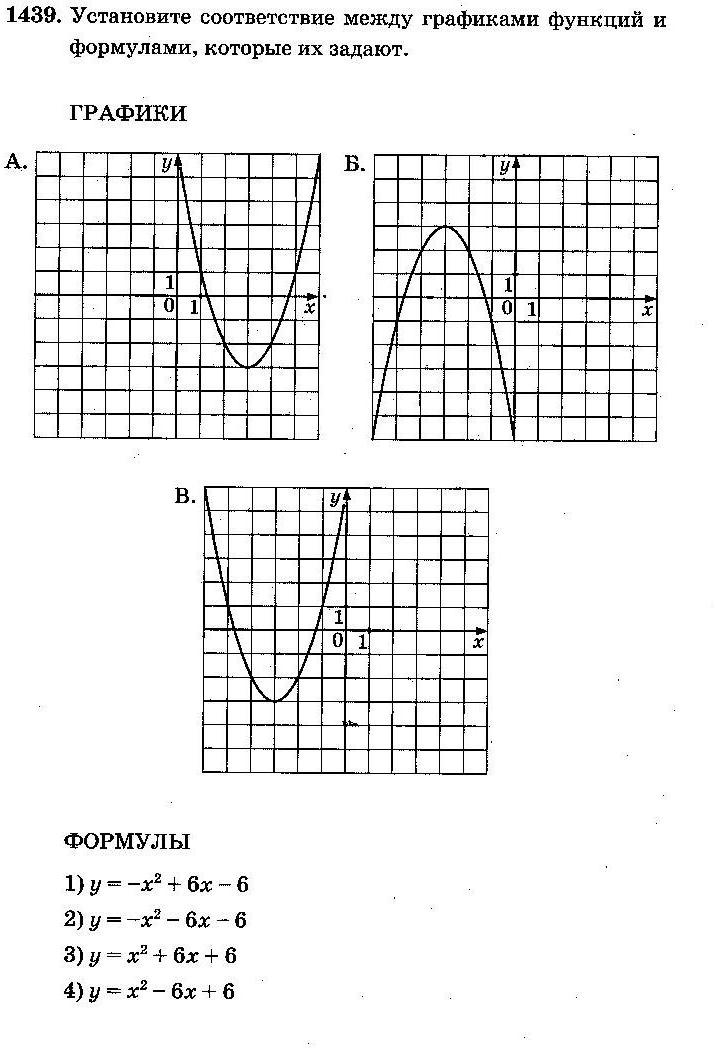
АЛГОРИТМ:

А. Ветви параболы направлены вверх (a>0), следовательно, подходят № 3 и № 4; вычислим абсциссу вершины параболы№ 3по формуле 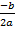x₀= : x₀= 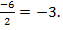Получаем, что это рисунок В. Аналогично вычислим абсциссу вершины параболы№ 4по формуле 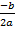x₀= : x₀= 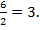Получаем, что это рисунок А.

Б. Ветви параболы направлены вниз (a<0), следовательно, подходят № 1 и № 2;

вычислим абсциссу вершины параболы№ 1по формуле 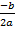x₀= : x₀= 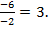Такого рисунка нет. Вычислим абсциссу вершины параболы№ 2по формуле 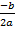x₀= : x₀= 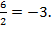Получаем, что это рисунок Б.

Ответ: А–4; Б–2; В–3

Реши самостоятельно:

3. y= – обратная пропорциональность. Графиком обратной пропорциональности является гипербола. Число k – коэффициент, k≠0.

Если k>0, то график расположен в I и III четверти

k<0, то график расположен во II и IV четверти

Задание 5 (тип 9)

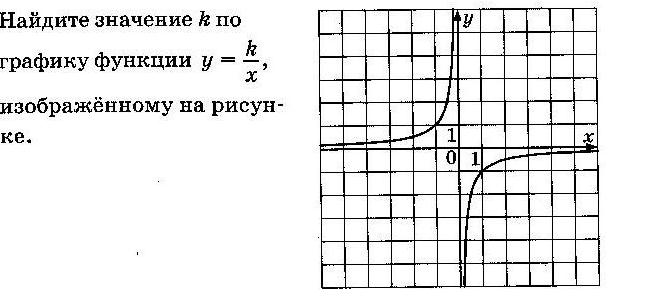
АЛГОРИТМ:

a. Так как график расположен во II и IV четверти, то k<0;

b. Выберем точку с целыми координатами, лежащую на графике, например, (–1;1). Подставим её координаты вместо x и y в уравнение y= . Получаем 1= 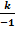.То есть

k =1×(–1).Отсюда следует, что k=–1.

Ответ: –1

Реши самостоятельно:

1.

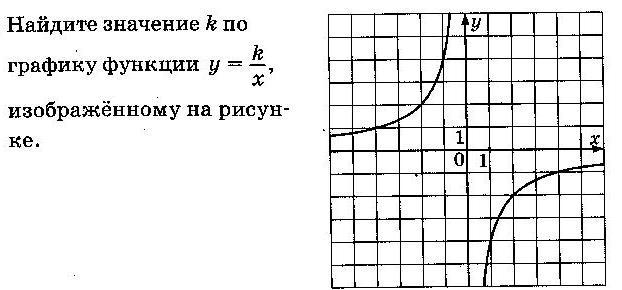
2.

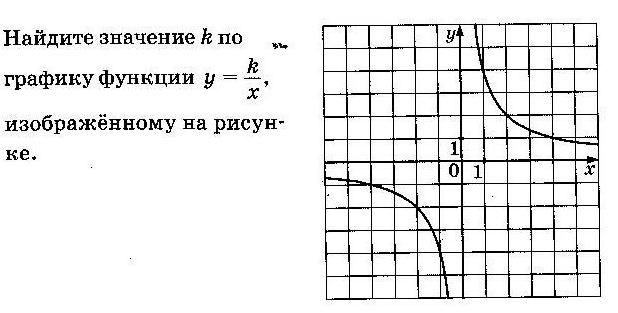
3.

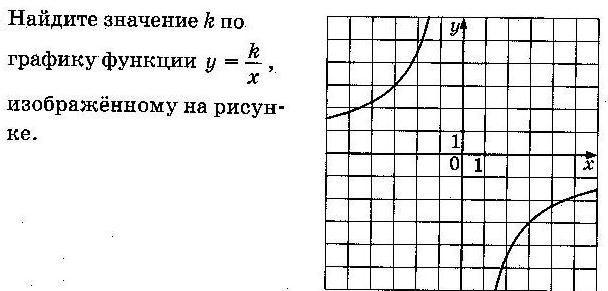
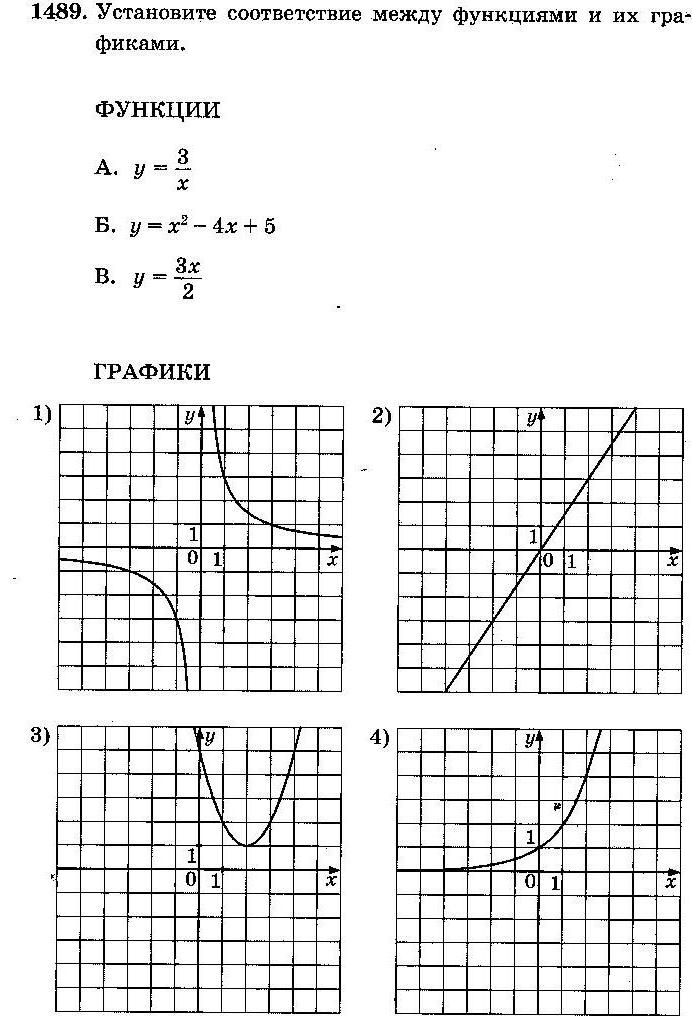
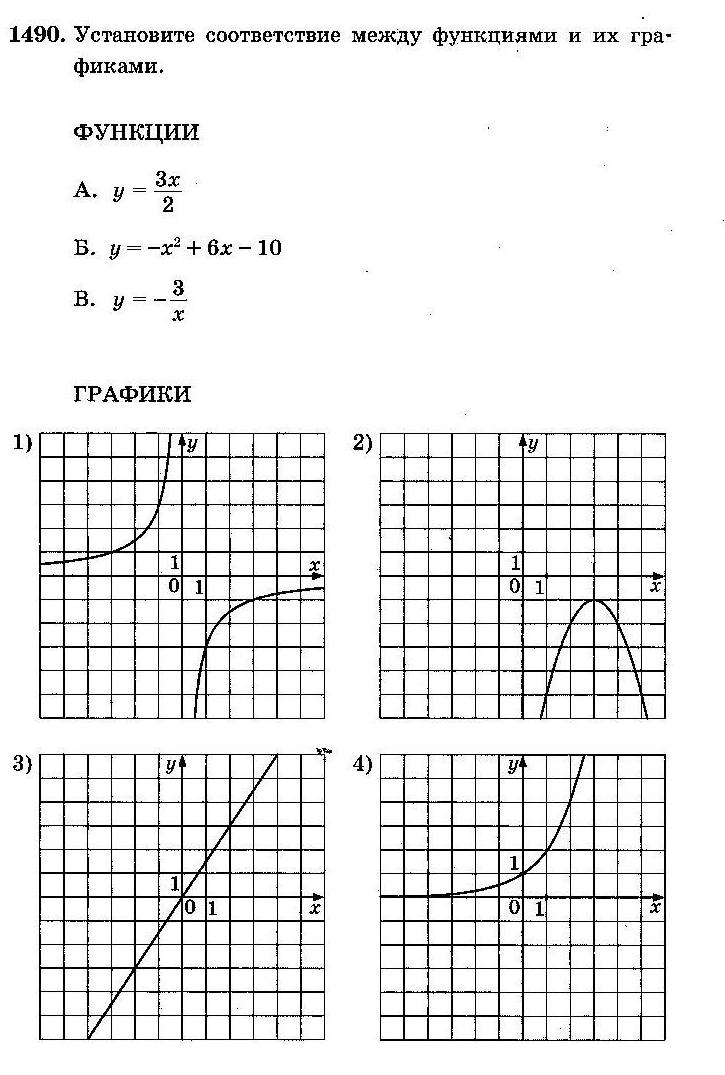
Задание 5 (тип 10)

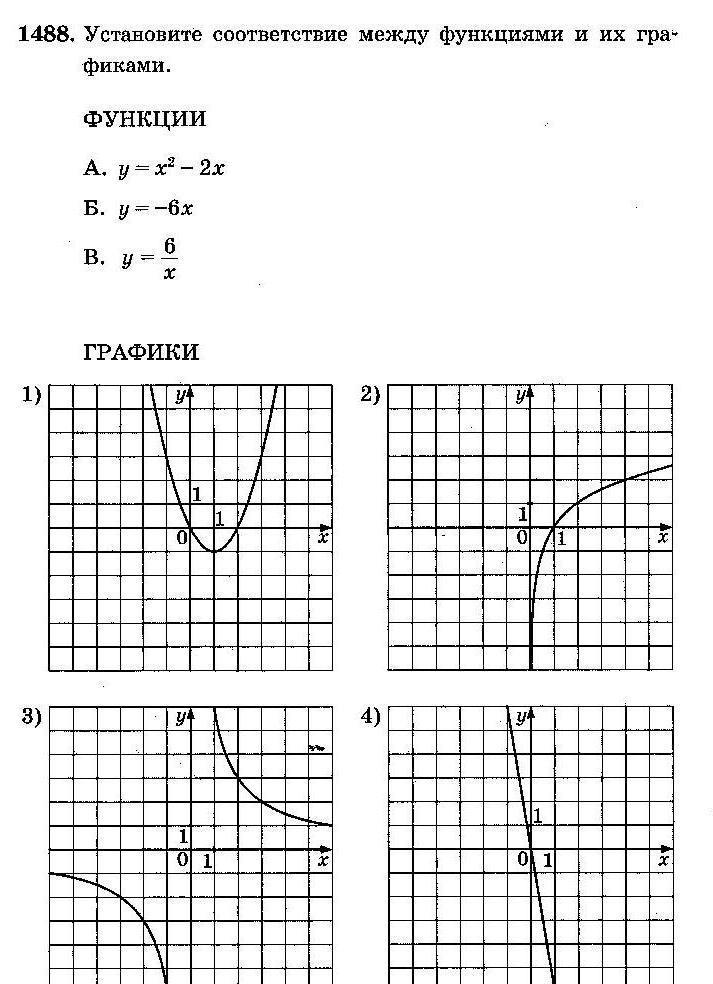
АЛГОРИТМ:

А. Это квадратичная функция, следовательно, её график – парабола, выбираем ответ 1);

Б. График прямой пропорциональности – прямая, проходящая через точку (0;0), выбираем ответ 4);

В. Это обратная пропорциональность, а её график – гипербола. Следует выбрать ответ 3)

Ответ: А–1; Б–4; В–3

Реши самостоятельно: