В пересечении гранных поверхностей плоскостями получаются многоугольники. Их вершины определяются как точки пересечения ребер гранных поверхностей с секущей плоскостью
Многоугольник сечения может быть построен двумя способами:
1. Вершины многоугольника нахо-дятся как точки пересечения прямых (ребер) с секущей плоскостью;
2. Стороны многоугольника нахо-дятся как линии пересечения граней (плоскостей) многогранника с секущей плоскостью.
На рис. 12.2 показано построение сечения пирамиды плоскостью S.
Секущая плоскость является фронтально-проецирующей, следовательно, все линии, лежащие в этой плоскости, совпадут с фронтальным следом S2 плоскости S. Следовательно, фронтальная проекция 122232 сечения определится при пересечении фронтальных проекций ребер пирамиды со следом S(S)2. Горизонтальные проекции точек 1(11), 2(21) и 3(31) находим из условия принадлежности точек ребрам пирамиды.
Пример 3. Построить линию пересечения цилиндрической поверхности вращения с плоскостью S(S)2 (рис. 12.3).
Решение. Вначале находим опорные точки A(A1, A2), B(B1, B2), C(C1, C2) и D(D1, D2). Точки А и В находятся в пересечении образующих фронтального контура поверхности и плоскости S (вначале определяем A2 и B2, а затем по линиям проекционной связи – A1 и B1). Точки С и D являются точками пересечения горизонтального контура поверхности и плоскости S. На П2 горизонтальный контур совпадает с проекцией оси поверхности вращения, а на П1 является очерком. Тогда вначале строим C2 и D2, а затем C1 и D1.
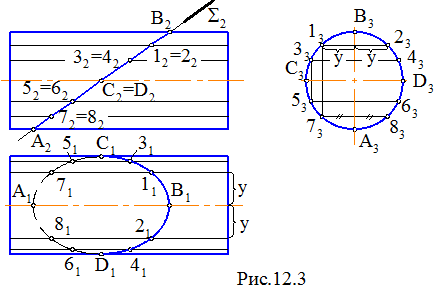
Точки 1(11, 12), 2(21, 22), …, 8(81, 82) – это промежуточные точки сечения. Они построены введением промежуточных прямолинейных образующих поверхности. Вначале проводим проекции образующих на П2, например через точки 12, 22 (образующие – фронтально конкурирующие). На П3 эти образующие проецируются в точки 13 и 23. Горизонтальные проекции образующих построены по двум заданным, как показано на рис. 12.3, отложив соответствующие значения координаты y.
12.2. Пересечение конической поверхности вращения плоскостью
В зависимости от направления секущей плоскости в сечении конической поверхности вращения могут получиться различные линии. Они называются коническими сечениями. На рис. 12.4 приведена фронтальная проекция конической поверхности вращения (ось i параллельна П2) и фронтально проецирующие плоскости 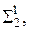
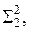 …,
…, 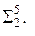 На рис. 12.5 показаны наглядные изображения результатов пересечения плоскостями тел, ограниченных конической поверхностью вращения.
На рис. 12.5 показаны наглядные изображения результатов пересечения плоскостями тел, ограниченных конической поверхностью вращения.
В результате пересечения конуса плоскостью, перпендикулярной оси конуса, получается окружность (рис. 12.4, а).
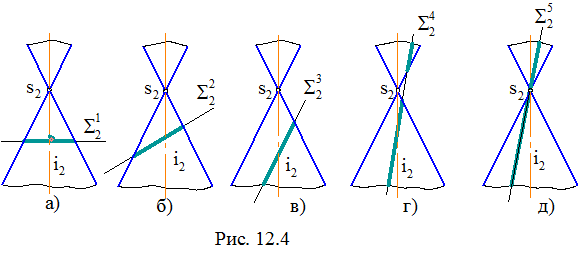
Эллипс получается в том случае, если секущая плоскость пересекает все образующие поверхности и не перпендикулярна оси i (рис. 12.4, б).
Плоскость 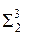 параллельна одной образующей поверхности и пересекает одну половину конической поверхности. Сечением является парабола (рис. 12.4, в).
параллельна одной образующей поверхности и пересекает одну половину конической поверхности. Сечением является парабола (рис. 12.4, в).
Плоскость 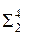 параллельна двум образующим и пересекает обе половины конической поверхности (сечение – гипербола) (рис. 12.4, г).
параллельна двум образующим и пересекает обе половины конической поверхности (сечение – гипербола) (рис. 12.4, г).
Плоскость 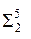 проходит через вершину конической поверхности (сечение – две пересекающиеся прямые) (рис. 12.4, д).
проходит через вершину конической поверхности (сечение – две пересекающиеся прямые) (рис. 12.4, д).

а) б) в) г) д)
Рис. 12.5
