Вероятность того, что деталь находится только в одном ящике, равна 1 страница
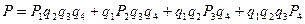
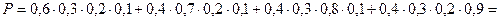
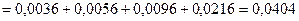
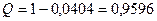
Вероятность того, что нужной деталь нет ни в одном ящике, равна:
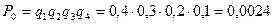
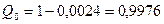
Искомая вероятность равна 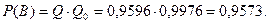
Формула полной вероятности.
Пусть некоторое событие А может произойти вместе с одним из несовместных событий 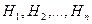 , составляющих полную группу событий. Пусть известны вероятности этих событий
, составляющих полную группу событий. Пусть известны вероятности этих событий 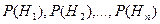 и условные вероятности наступления события А при наступлении события Hi
и условные вероятности наступления события А при наступлении события Hi 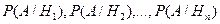 .
.
 Теорема. Вероятность события А, которое может произойти вместе с одним из событий
Теорема. Вероятность события А, которое может произойти вместе с одним из событий 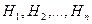 , равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
, равна сумме парных произведений вероятностей каждого из этих событий на соответствующие им условные вероятности наступления события А.
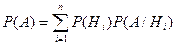
Фактически эта формула полной вероятностиуже использовалась при решении примеров, приведенных выше, например, в задаче с револьвером.
Доказательство.
Т.к. события 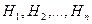 образуют полную группу событий, то событие А можно представить в виде следующей суммы:
образуют полную группу событий, то событие А можно представить в виде следующей суммы:
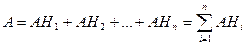
Т.к. события 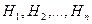 несовместны, то и события AHi тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:
несовместны, то и события AHi тоже несовместны. Тогда можно применить теорему о сложении вероятностей несовместных событий:
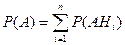
При этом 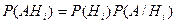
Окончательно получаем: 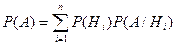
Теорема доказана.
Пример. Один из трех стрелков производит два выстрела. Вероятность попадания в цель при одном выстреле для первого стрелка равна 0,4, для второго – 0,6, для третьего – 0,8. Найти вероятность того, что в цель попадут два раза.
Вероятность того, что выстрелы производит первый, второй или третий стрелок равна 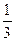 .
.
Вероятности того, что один из стрелков, производящих выстрелы, два раза попадает в цель, равны:
- для первого стрелка: 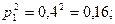
- для второго стрелка: 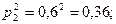
- для третьего стрелка: 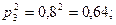
Искомая вероятность равна:
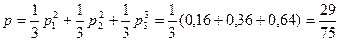
ЛЕКЦИЯ 2.
Формула Бейеса. (формула гипотез)
Пусть имеется полная группа несовместных гипотез 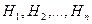 с известными вероятностями их наступления
с известными вероятностями их наступления 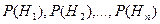 . Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности
. Пусть в результате опыта наступило событие А, условные вероятности которого по каждой из гипотез известны, т.е. известны вероятности 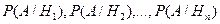 .
.
Требуется определить какие вероятности имеют гипотезы 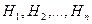 относительно события А, т.е. условные вероятности
относительно события А, т.е. условные вероятности 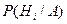 .
.
 Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
Теорема. Вероятность гипотезы после испытания равна произведению вероятности гипотезы до испытания на соответствующую ей условную вероятность события, которое произошло при испытании, деленному на полную вероятность этого события.
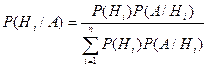
Эта формула называется формулой Бейеса.
Доказательство.
По Теореме умножения вероятностей получаем:
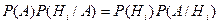
Тогда если 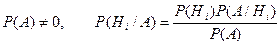 .
.
Для нахождения вероятности P(A) используем формулу полной вероятности.
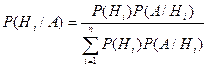
Если до испытания все гипотезы равновероятны с вероятностью 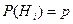 , то формула Бейеса принимает вид:
, то формула Бейеса принимает вид:

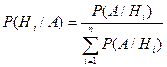
Повторение испытаний.
Формула Бернулли.
Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.
Допустим, что событие А наступает в каждом испытании с вероятностью Р(А)=р. Определим вероятность Рт,п того, что в результате п испытаний событие А наступило ровно т раз.
Эту вероятность в принципе можно посчитать, используя теоремы сложения и умножения вероятностей, как это делалось в рассмотренных выше примерах. Однако, при достаточно большом количестве испытаний это приводит к очень большим вычислениям. Таким образом, возникает необходимость разработать общий подход к решению поставленной задачи. Этот подход реализован в формуле Бернулли. (Якоб Бернулли (1654 – 1705) – швейцарский математик)
Пусть в результате п независимых испытаний, проведенных в одинаковых условиях, событие А наступает с вероятностью Р(А) = р, а противоположное ему событие 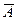 с вероятностью
с вероятностью 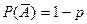 .
.
Обозначим Ai – наступление события А в испытании с номером i. Т.к. условия проведения опытов одинаковые, то эти вероятности равны.
Если в результате п опытов событие А наступает ровно т раз, то остальные п-т раз это событие не наступает. Событие А может появиться т раз в п испытаниях в различных комбинациях, число которых равно количеству сочетаний из п элементов по т. Это количество сочетаний находится по формуле:
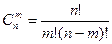
Вероятность каждой комбинации равна произведению вероятностей:
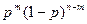
 Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:
Применяя теорему сложения вероятностей несовместных событий, получаем формулу Бернулли:
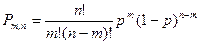
Формула Бернулли важна тем, что справедлива для любого количества независимых испытаний, т.е. того самого случая, в котором наиболее четко проявляются законы теории вероятностей.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятность того, что в цель попали не менее трех раз.
Вероятность не менее трех попаданий складывается из вероятности пяти попаданий, четырех попаданий и трех попаданий.
Т.к. выстрелы независимы, то можно применить формулу Бернулли вероятности того, что в т испытаниях событие в вероятностью р наступает ровно п раз.
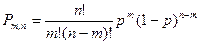
В случае пяти попаданий из пяти возможных:
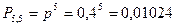
Четыре попадания из пяти выстрелов:
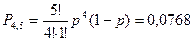
Три попадания из пяти:
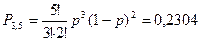
Окончательно, получаем вероятность не менее трех попаданий из пяти выстрелов:
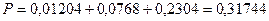
Случайные величины.
Выше рассматривались случайные события, являющиеся качественной характеристикой случайного результата опыта. Для получения количественной характеристики вводится понятие случайной величины.
Определение. Случайной величинойназывается величина, которая в результате опыта может принимать то или иное значение, причем заранее известно какое именно.
Случайные величины можно разделить на две категории.
Определение. Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).
Это множество может быть как конечным, так и бесконечным.
Например, количество выстрелов до первого попадания в цель является дискретной случайной величиной, т.к. эта величина может принимать и бесконечное, хотя и счетное количество значений.
Определение. Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.
Очевидно, что число возможных значений непрерывной случайной величины бесконечно.
Для задания случайной величины недостаточно просто указать ее значение, необходимо также указать вероятность этого значения.
Закон распределения дискретной случайной величины.
Определение. Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.
Закон распределения может быть задан аналитически, в виде таблицы или графически.
Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.
Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.
Пример. По цели производится 5 выстрелов. Вероятность попадания для каждого выстрела равна 0,4. Найти вероятности числа попаданий и построить многоугольник распределения.
Вероятности пяти попаданий из пяти возможных, четырех из пяти и трех из пяти были найдены выше по формуле Бернулли и равны соответственно:
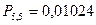 ,
, 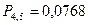 ,
, 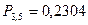
Аналогично найдем:
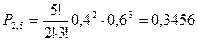
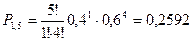
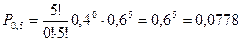
Представим графически зависимость числа попаданий от их вероятностей.
 |
При построении многоугольника распределения надо помнить, что соединение полученных точек носит условный характер. В промежутках между значениями случайной величины вероятность не принимает никакого значения. Точки соединены только для наглядности.
Пример. Вероятность хотя бы одного попадания в мишень стрелком при трех выстрелах равна 0,875. Найти вероятность попадания в мишень при одном выстреле.
Если обозначить р – вероятность попадания стрелком в мишень при одном выстреле, то вероятность промаха при одном выстреле, очевидно, равна (1 – р).
Вероятность трех промахов из трех выстрелов равна (1 – р)3. Эта вероятность равна 1 – 0,875 = 0,125, т.е. в цель не попадают ни одного раза.
Получаем: 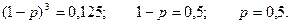
Пример. В первой коробке содержится 10 шаров, из них 8 белых; во второй коробке 20 шаров, из них 4 белых. Из каждой коробки наугад извлекли по одному шару, а затем из этих двух шаров наугад берут один шар. Найти вероятность того, что этот шар белый.
Вероятность того, что взятый из первой коробки шар белый - 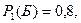 что не белый -
что не белый - 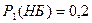 .
.
Вероятность того, что взятый из второй коробки шар белый - 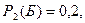 что не белый -
что не белый - 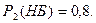
Вероятность того, что повторно выбран шар, извлеченный из первой коробки и вероятность того, что повторно выбран шар, извлеченный из второй коробки, равны 0,5.
Вероятность того, что повторно выбран шар, извлеченный из первой коробки, и он белый - 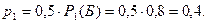
Вероятность того, что повторно выбран шар, извлеченный из второй коробки, и он белый - 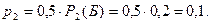
Вероятность того, что повторно будет выбран белый шар, равна
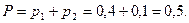
Пример. Имеется пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит цель при выстреле из винтовки с оптическим прицелом, равна 0,95, для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что цель будет поражена, если стрелок произведет один выстрел из наугад выбранной винтовки.
Вероятность того, что выбрана винтовка с оптическим прицелом, обозначим 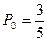 , а вероятность того, что выбрана винтовка без оптического прицела, обозначим
, а вероятность того, что выбрана винтовка без оптического прицела, обозначим 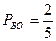 .
.
Вероятность того, что выбрали винтовку с оптическим прицелом, и при этом цель была поражена 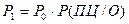 , где Р(ПЦ/O) – вероятность поражения цели из винтовки с оптическим прицелом.
, где Р(ПЦ/O) – вероятность поражения цели из винтовки с оптическим прицелом.
Аналогично, вероятность того, что выбрали винтовку без оптического прицела, и при этом цель была поражена 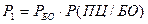 , где Р(ПЦ/БO) – вероятность поражения цели из винтовки без оптического прицела.
, где Р(ПЦ/БO) – вероятность поражения цели из винтовки без оптического прицела.
Окончательная вероятность поражения цели равна сумме вероятностей Р1 и Р2, т.к. для поражения цели достаточно, чтобы произошло одно из этих несовместных событий.
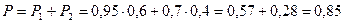
Пример. Трое охотников одновременно выстрелили по медведю, который был убит одной пулей. Определить вероятность того, что медведь был убит первым стрелком, если вероятности попадания для этих стрелков равны соответственно 0,3, 0,4, 0,5.
В этой задаче требуется определить вероятность гипотезы уже после того, как событие уже совершилось. Для определения искомой вероятности надо воспользоваться формулой Бейеса. В нашем случае она имеет вид:
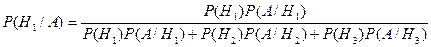
В этой формуле Н1, Н2, Н3 – гипотезы, что медведя убьет первый, второй и третий стрелок соответственно. До произведения выстрелов эти гипотезы равновероятны и их вероятность равна 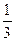 .
.
P(H1/A) – вероятность того, что медведя убил первый стрелок при условии, что выстрелы уже произведены (событие А).
Вероятности того, что медведя убьет первый, второй или третий стрелок, вычисленные до выстрелов, равны соответственно:
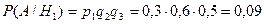
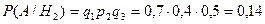
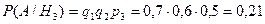
Здесь q1 = 0,7; q2 = 0,6; q3 = 0,5 – вероятности промаха для каждого из стрелков, рассчитаны как q = 1 – p, где р – вероятности попадания для каждого из стрелков.
Подставим эти значения в формулу Бейеса:
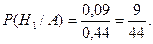
Пример. Последовательно послано четыре радиосигнала. Вероятности приема каждого из них не зависят от того, приняты ли остальные сигналы, или нет. Вероятности приема сигналов равны соответственно 0,2, 0,3, 0,4, 0,5. Определить вероятность приема трех радиосигналов.
Событие приема трех сигналов из четырех возможно в четырех случаях:
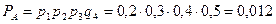
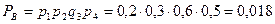
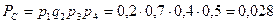
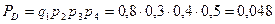
Для приема трех сигналов необходимо совершение одного из событий А, В, С или D. Таким образом, находим искомую вероятность:
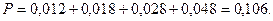
Пример. Двадцать экзаменационных билетов содержат по два вопроса, которые не повторяются. Экзаменующийся знает ответы только на 35 вопросов. Определить вероятность того, что экзамен будет сдан, если для этого достаточно ответить на два вопроса одного билета или на один вопрос одного билета и на указанный дополнительный вопрос из другого билета.
В общей сложности имеется 40 вопросов (по 2 в каждом из 20 билетов). Вероятность того, что выпадает вопрос, на который ответ известен, очевидно, равна 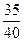 .
.
Для того, чтобы сдать экзамен, требуется совершение одного из трех событий:
1) Событие A – ответили на первый вопрос (вероятность 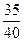 ) и ответили на второй вопрос (вероятность
) и ответили на второй вопрос (вероятность 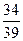 ). Т.к. после успешного ответа на первый вопрос остается еще 39 вопросов, на 34 из которых ответы известны.
). Т.к. после успешного ответа на первый вопрос остается еще 39 вопросов, на 34 из которых ответы известны.
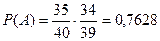
2) Событие В – на первый вопрос ответили (вероятность 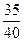 ), на второй – нет (вероятность
), на второй – нет (вероятность 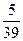 ), на третий – ответили (вероятность
), на третий – ответили (вероятность 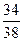 ).
).
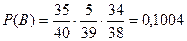
3) Событие С – на первый вопрос не ответили (вероятность 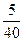 ), на второй – ответили (вероятность
), на второй – ответили (вероятность 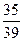 ), на третий – ответили (вероятность
), на третий – ответили (вероятность 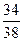 ).
).
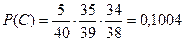
Вероятность того, что при заданных условиях экзамен будет сдан равна:
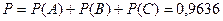
Пример. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой и второй партий извлекают по две детали. Какова вероятность того, что среди них нет бракованных деталей.
Вероятность оказаться не бракованной для первой детали, извлеченной из первой партии, равна 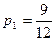 , для второй детали, извлеченной из первой партии при условии, что первая деталь была не бракованной -
, для второй детали, извлеченной из первой партии при условии, что первая деталь была не бракованной - 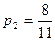 .
.
Вероятность оказаться не бракованной для первой детали, извлеченной из второй партии, равна 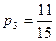 , для второй детали, извлеченной из второй партии при условии, что первая деталь была не бракованной -
, для второй детали, извлеченной из второй партии при условии, что первая деталь была не бракованной - 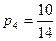 .
.
Вероятность того, что среди четырех извлеченных деталей нет бракованных, равна:
.
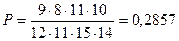
Рассмотрим тот же пример, но несколько с другим условием.
Пример. Имеются две партии однородных деталей. Первая партия состоит из 12 деталей, 3 из которых - бракованные. Вторая партия состоит из 15 деталей, 4 из которых – бракованные. Из первой партии извлекаются наугад 5 деталей, а из второй – 7 деталей. Эти детали образуют новую партию. Какова вероятность достать из них бракованную деталь?
Для того, чтобы выбранная наугад деталь была бы бракованной, необходимо выполнение одного из двух несовместных условий:
1) Выбранная деталь была из первой партии (вероятность - 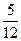 ) и при этом она – бракованная (вероятность -
) и при этом она – бракованная (вероятность - 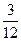 ). Окончательно:
). Окончательно:
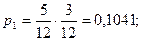
2) Выбранная деталь была из второй партии (вероятность - 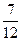 ) и при этом она – бракованная (вероятность -
) и при этом она – бракованная (вероятность - 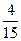 ). Окончательно:
). Окончательно:
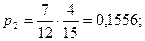
Окончательно, получаем: 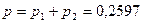 .
.
Пример. В урне 3 белых и 5 черных шаров. Из урны вынимают наугад два шара. Найти вероятность того, что эти шары не одного цвета.
Событие, состоящее в том, что выбранные шары разного цвета произойдет в одном из двух случаев:
1) Первый шар белый (вероятность - 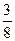 ), а второй – черный (вероятность -
), а второй – черный (вероятность - 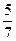 ).
).
2) Первый шар черный (вероятность - 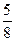 ), а второй – белый (вероятность -
), а второй – белый (вероятность - 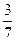 ).
).
Окончательно получаем: 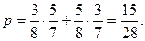
Биноминальное распределение.
Если производится п независимых испытаний, в каждом из которых событие А может появиться с одинаковой вероятностью р в каждом из испытаний, то вероятность того, что событие не появится, равна q = 1 – p.
Примем число появлений события в каждом из испытаний за некоторую случайную величину Х.
Чтобы найти закон распределения этой случайной величины, необходимо определить значения этой величины и их вероятности.
Значения найти достаточно просто. Очевидно, что в результате п испытаний событие может не появиться вовсе, появиться один раз, два раза, три и т.д. до п раз.
Вероятность каждого значения этой случайной величины можно найти по формуле Бернулли.

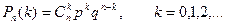
Эта формула аналитически выражает искомый закон распределения. Этот закон распределения называется биноминальным.
Пример. В партии 10% нестандартных деталей. Наугад отобраны 4 детали. Написать биноминальный закон распределения дискретной случайной величины Х – числа нестандартных деталей среди четырех отобранных и построить многоугольник полученного распределения.
Вероятность появления нестандартной детали в каждом случае равна 0,1.
Найдем вероятности того, что среди отобранных деталей:
1) Вообще нет нестандартных.
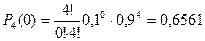
2) Одна нестандартная.
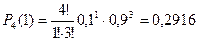
3) Две нестандартные детали.
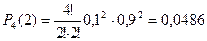
4) Три нестандартные детали.
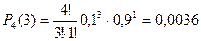
5) Четыре нестандартных детали.
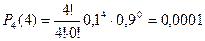
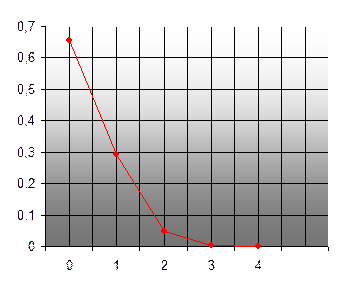 |
Построим многоугольник распределения.
