Электродинамика веществ с отрицательным показателем преломления
Кратко опишем рассуждения Веселаго, на основании которых он создал свою фундаментальную теорию.
Итак, основное выражение для анализа – это формула , хорошо известная по теории электромагнитного поля дисперсионное уравнение:

Если вещество изотропно, то уравнение упрощается:

Всегда молчаливо принималось, что значение  есть заведомо положительное число, но с математической точки зрения, это не так. Более того, значения
есть заведомо положительное число, но с математической точки зрения, это не так. Более того, значения  и
и  , стоящие под корнем, также всегда считались положительными, хотя, вообще говоря, давно известно, что величина диэлектрической проницаемости для плазмы
, стоящие под корнем, также всегда считались положительными, хотя, вообще говоря, давно известно, что величина диэлектрической проницаемости для плазмы  может быть и отрицательной, точно также как и для ферритов, значение магнитной проницаемости может быть отрицательным. Всегда было ясно, что если под корнем в один из сомножителей станет отрицательным, то величина
может быть и отрицательной, точно также как и для ферритов, значение магнитной проницаемости может быть отрицательным. Всегда было ясно, что если под корнем в один из сомножителей станет отрицательным, то величина  окажется мнимой, и распространение волн в среде с мнимым
окажется мнимой, и распространение волн в среде с мнимым  заменится отражением.
заменится отражением.
Удивительно то, что до Веселаго никто не задавался вопросом, что будет, если в оба сомножителя будут отрицательными. Он показал [1-3], что при отрицательных и  нужно брать и для
нужно брать и для  отрицательное значение. Были сразу сформулированы весьма интересные и необычные электродинамические свойства веществ, обладающих отрицательным преломлением.
отрицательное значение. Были сразу сформулированы весьма интересные и необычные электродинамические свойства веществ, обладающих отрицательным преломлением.
Для того чтобы выявить электродинамические закономерности, обратимся к уравнениям Максвелла и материальным уравнениям :


В приближении плоской монохроматической волны, как уже было показано в ходе курса, материальные уравнения можно записать в следующем виде:

Из выражений сразу же видно, что если  и
и  , то
, то  образуют правую тройку векторов, а если
образуют правую тройку векторов, а если  и
и  - левую. Если ввести для векторов
- левую. Если ввести для векторов  направляющие косинусы и обозначить их как
направляющие косинусы и обозначить их как  соответственно, то волна, распространяющаяся в данной среде, будет характеризоваться матрицей
соответственно, то волна, распространяющаяся в данной среде, будет характеризоваться матрицей 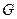 :
:

Определитель этой матрицы равен +1, если тройка векторов  правая, и -1, если эта тройка правая. Обозначив этот определитель через
правая, и -1, если эта тройка правая. Обозначив этот определитель через  , можно сказать, что
, можно сказать, что  характеризует “правизну” данной среды. Элементы матрицы удовлетворяют соотношению:
характеризует “правизну” данной среды. Элементы матрицы удовлетворяют соотношению:

Здесь  - алгебраические дополнения элемента
- алгебраические дополнения элемента  . Поток энергии, переносимой волной, определяется вектором Пойнтинга
. Поток энергии, переносимой волной, определяется вектором Пойнтинга  , который равен
, который равен

Вектор  в соответствии с всегда образует с векторами
в соответствии с всегда образует с векторами 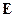 и
и 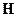 правую тройку векторов. Таким образом, для правых веществ вектора
правую тройку векторов. Таким образом, для правых веществ вектора  и
и 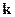 направлены в одну сторону, а для левых – в разные.
направлены в одну сторону, а для левых – в разные.
Именно поэтому в англоязычной литературе такие материалы называются Left-Handed-Materials (Medium) или кратко LHM .
Рассмотрим, как же ведет себя свет на границе раздела правых и левых веществ (рис.1).

Рис. 1. Преломление света на границе двух сред. Путь 1-4 соответствует ходу падающего и преломленного лучей для случая  , а путь 1-3 – для случая
, а путь 1-3 – для случая  .
.
Преломление света, как известно, описывается законом Снеллиуса:

Если, без нарушения общности, положить  , то привычный ход луча при преломлении соответствует пути 1-4. Если же наш луч идет по пути 1-3, то такой путь преломленного луча будет удовлетворять закону Снеллиуса при
, то привычный ход луча при преломлении соответствует пути 1-4. Если же наш луч идет по пути 1-3, то такой путь преломленного луча будет удовлетворять закону Снеллиуса при  .
.
Для материалов с  характерна необычная реализация не только закона Снеллиуса, но и ряда других явлений электродинамики, в частности эффектов Доплера и Черенкова, формул Френеля, принципа Ферма.
характерна необычная реализация не только закона Снеллиуса, но и ряда других явлений электродинамики, в частности эффектов Доплера и Черенкова, формул Френеля, принципа Ферма.

Рис. 2. Распространение света через пластину из LHM
Большинство формул электродинамики нужно переписывать, так как не во все формулы входим именно  . Часто рассматриваются немагнитные приближения, полагая
. Часто рассматриваются немагнитные приближения, полагая  . Поэтому выражения для LHM нужно уточнять.
. Поэтому выражения для LHM нужно уточнять.
На основании закона Снеллиуса и законов геометрической оптики можно рассмотреть как будет действовать пластинка, линза из LHM. На рис. 2 показано распространение света сквозь плоскопараллельную пластину, выполненную из материала с  . Такая пластина, способна фокусировать в точку изучение, выходящее из точечного источника, расположенного по другую сторону пластины, что не даст пластина из обычного материала.
. Такая пластина, способна фокусировать в точку изучение, выходящее из точечного источника, расположенного по другую сторону пластины, что не даст пластина из обычного материала.
Что касается настоящих линз, ход лучей через них изображен на рис. 3. Как видно, выпуклая и вогнутая линза будто “поменялись местами”, так как выпуклая линза является рассеивающей, а вогнутая – собирающей.

Рис. 3. Ход лучей через линзы из LHM
