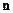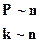Теорема Пойнтинга (Закон сохранения энергии электромагнитных волн в форме уравнения непрерывности). Теорема Пойнтинга с учётом диссипации для среды
Будем рассматривать случай вакуума. Уравнения Максвелла для электромагнитных волн в вакууме имеют вид:
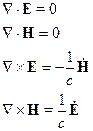
Далее значок  будет означать, что оператор
будет означать, что оператор 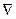 действует на
действует на 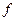 .
.
Умножим третье уравнение на 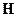 , а четвёртое на
, а четвёртое на 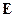 скалярно. Тогда:
скалярно. Тогда:
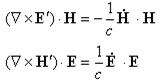
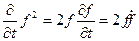
Тогда:
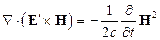 (19.1)
(19.1)
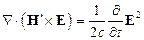 (19.2)
(19.2)
Вычтем из (19.1) – (19.2), тогда получим:
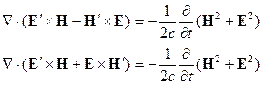
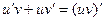 , следовательно
, следовательно 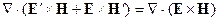
Введём обозначение 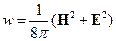 - объёмная плотность в СГС. И введём вектор Пойнтинга.
- объёмная плотность в СГС. И введём вектор Пойнтинга.
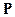 - плотность потока энергии электромагнитного поля.
- плотность потока энергии электромагнитного поля.
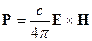 - в СГС.
- в СГС.
Тогда 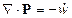
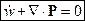 - уравнение непрерывности
- уравнение непрерывности
В случае среды 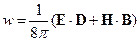
Если проинтегрировать по объёму, то:
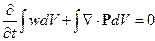 (19.3)
(19.3)
По теореме Остроградского-Гаусса: 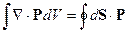
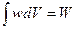 - энергия электромагнитного поля, заключенная в объём
- энергия электромагнитного поля, заключенная в объём 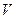 с поверхностью
с поверхностью 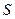 .
.
Тогда (19.3) перепишется в виде:
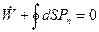
Если это выражение поделить на площадь 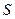 , то получим, что
, то получим, что 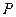 - это энергия, переносимая в единицу времени через единицу поверхности. Физическое содержание этого уравнения – закон сохранения энергии.
- это энергия, переносимая в единицу времени через единицу поверхности. Физическое содержание этого уравнения – закон сохранения энергии.
Если рассматривать объём 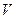 и если угол между нормалью
и если угол между нормалью 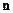 и
и 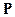 острый, то интеграл
острый, то интеграл 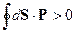 , т.е. происходит вытекание энергии из объёма
, т.е. происходит вытекание энергии из объёма 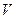 . В этом случае
. В этом случае
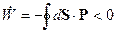
Т.е. происходит убывание 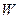 в замкнутом объёме
в замкнутом объёме 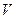 за счёт переноса её через поверхность объёма во вне.
за счёт переноса её через поверхность объёма во вне.
Теорема Пойнтинга с учётом диссипации для среды.
Умножим третье уравнение Максвелла скалярно на 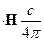 , а четвёртое скалярно на
, а четвёртое скалярно на 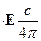 и вычитая из третьего уравнения четвёртое получим:
и вычитая из третьего уравнения четвёртое получим:
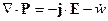
где 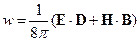 ,
, 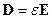 и
и 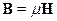 . Тогда:
. Тогда:
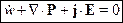 -Теорема Пойнтинга в полном виде.
-Теорема Пойнтинга в полном виде.
Третье слагаемое описывает процессы диссипации.
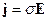 , тогда
, тогда 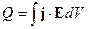 - закон Джоуля-Ленца.
- закон Джоуля-Ленца.
15 § 20. Соотношение между векторами 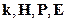 в случае плоских электромагнитных волн в вакууме
в случае плоских электромагнитных волн в вакууме
В случае плоских волн эти функции есть функции аргументов 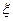 и
и 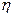 ;
; 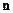 - нормаль к поверхности фронта волны.
- нормаль к поверхности фронта волны.
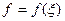 ,
, 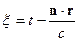
Вектор 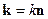 - волновой вектор, где
- волновой вектор, где 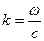 - волновое число. Запишем соотношения:
- волновое число. Запишем соотношения:
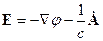
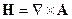
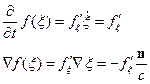
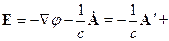
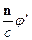
Первое слагаемое содержит и поперечную и продольную составляющую. Второе слагаемое приводит к продольной составляющей. Чтобы в поле 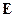 не было продольных составляющих надо положить
не было продольных составляющих надо положить 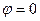 и надо
и надо 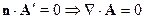 , т.е. чтобы поле было только поперечным нужно ввести калибровку:
, т.е. чтобы поле было только поперечным нужно ввести калибровку:
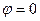
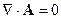
Вообще-то 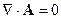 следует из уравнения Максвелла
следует из уравнения Максвелла 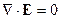 .
.
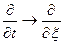
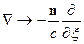
Рассмотрим теперь:
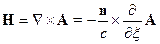
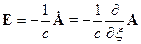
Тогда:
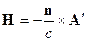
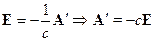
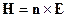
Т.е. 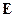 и
и 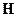 ортогональны. Более того
ортогональны. Более того 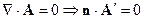
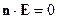
Т.е. 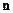 и
и 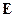 ортогональны. В результате образовалась правая тройка векторов. Ортогональность вектора
ортогональны. В результате образовалась правая тройка векторов. Ортогональность вектора 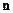 векторам
векторам 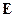 и
и 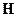 означает поперечность волны.
означает поперечность волны.
Рассмотрим вектор Пойнтинга:
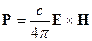
Для поперечных волн 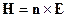 , тогда:
, тогда:
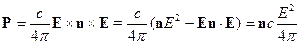
Найдём выражение для 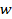 , выраженное через одно из полей:
, выраженное через одно из полей:
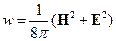
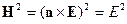
Тогда
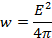
Связь вектора Пойнтинга с плотностью энергии:
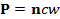
Значит, 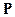 направлен по вектору нормали распространения фронта волны
направлен по вектору нормали распространения фронта волны