Примеры старайтесь решать самостоятельно!

Контрольная работа № 3.

Пояснение.

Контрольная работа № 3 состоит из 2-х частей.

Первую часть выполняют все студенты.

Вторая часть выполняется по вариантам. Вариант определяется по списку в журнале.

ПЕРВАЯ ЧАСТЬ

КОНТРОЛЬНОЙ РАБОТЫ.

Вычислить каждому все интегралы.

Задача 1. Найти интеграл .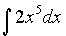

Задача 2. Найти интеграл .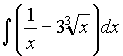

Задача 3. Найти интеграл .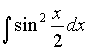

Задача 4. Найти интеграл .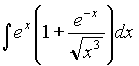

Задача 5. Найти интеграл .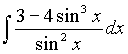

Задача 6. Найти интеграл .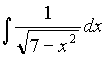

Задача 7. Найти интеграл .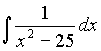

Задача 8. Найти интеграл .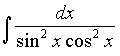

Задача 9. Найти интеграл .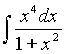

Задача 10 Найти интеграл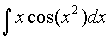

Задача 12. Найти интеграл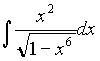

Задача 13. Найти интеграл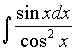

Задача 14. Найти интеграл .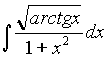

Задача 15. Найти интеграл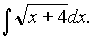

Задача 16. Найти интеграл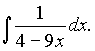

Задача 17. Найти интеграл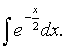

Задача 18. Найти интеграл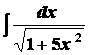

Задача 19. Найти интеграл .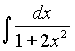

Задача 20. Найти интеграл .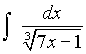

Задача 21. Найти интеграл .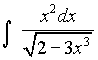

Задача 22. Найти интеграл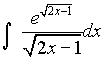

Задача 23. Найти интеграл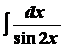

Решить каждому студенту все ДУ.

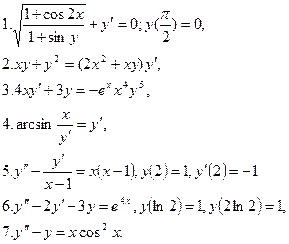
Вычислить каждому студенту все производные..

1. y=x⁴+3x²-2x+1 12. y=7x⁷+3x²-4x - 1

2. y=³ 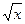+ 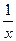- 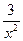+4 14. y= ⁴ 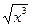+ 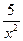- 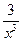+2

12. y=4x⁵ -3sin x+5ctgx 16. y= 3 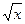+ 4 cosx-2 ctgx +3

19. y=3+ 4x² +⁵ 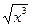+ + 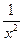sinx+ cosx

4. y=⁸ 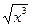-4x⁶ + 5ln x – 7cos x+ tgx+ctg x

5. y=log₂ x + 3 log₃x 20. y=4 e^x+ arctgx+ arcsinx

6. y=e^x- 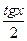+ 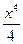22. y=5^x+6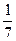^x+ ( )^x

7. y=arcsinx +3³ 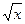+ 5 arccos x 24. y=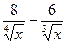

8. y=tg x- ctg x 26. y=arctg x- arcctg x

9. y=x cos x 28. y=x²tg x

10. y= 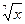ln x 11. y=x arccosx

31. y= 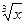arcctg x 32. y= x²log₃x

13. y= 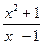34. y= 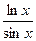+x ctg x

14. y = 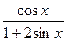15. y=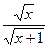

16. y = 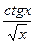17. y=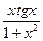

18. y= 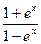40. y= 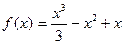, найти

f ’ (0), f ’ (1), f ’ (-1)

20. f (x)= x²- 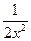, найти 42. f (x)= 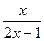, найти

f ' (2) – f ‘ (-2) f ' (0), f ‘ (2), f ’ (-2)

21. f (x)= 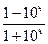, найти f ‘ (0)

22. f (x)= 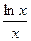, найти f ‘ (e),

f ‘ ( 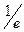), f ‘ (e)

23. f (x)=xln x, найти f ‘ (1), f ‘ (e), 46. y=sin 3 x

f ‘ (1/e), f ‘ (1/e²),

Вторая часть контрольной работы.

В этой части выбирается свой вариант.

Вычислите неопределенные интегралы:

1. 1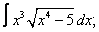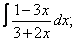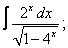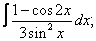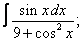
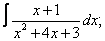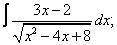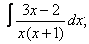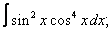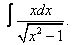2. 2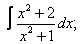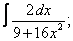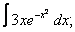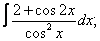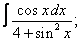
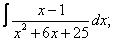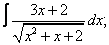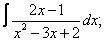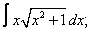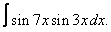3. 3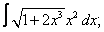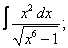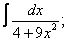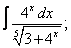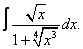
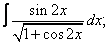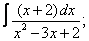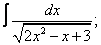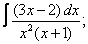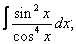4. 4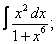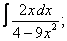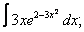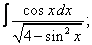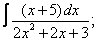
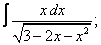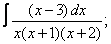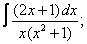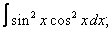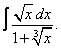5. 5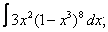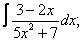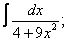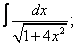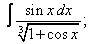
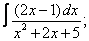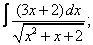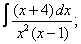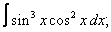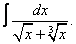6. 6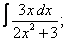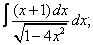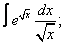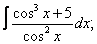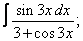
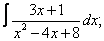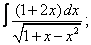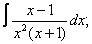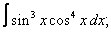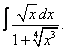7. 7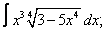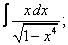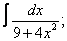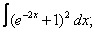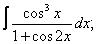
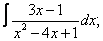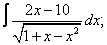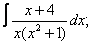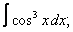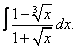8. 8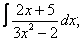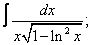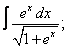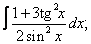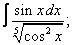
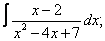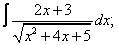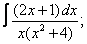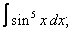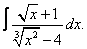9. 9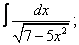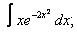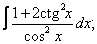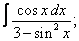
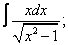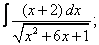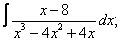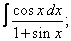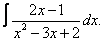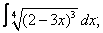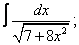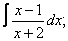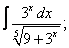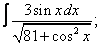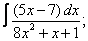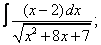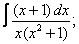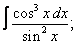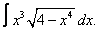111.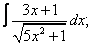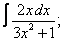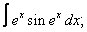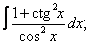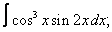
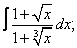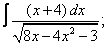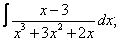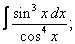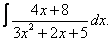112.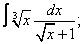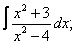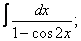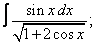
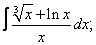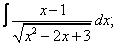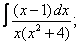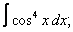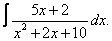113.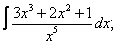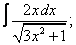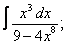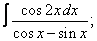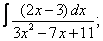
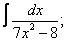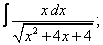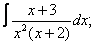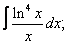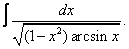114.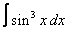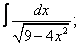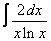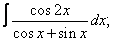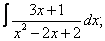
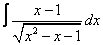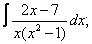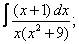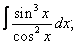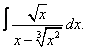115.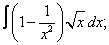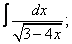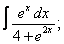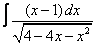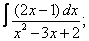
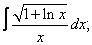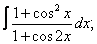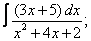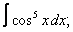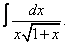116.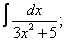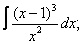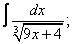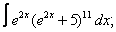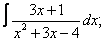
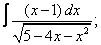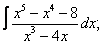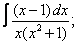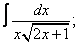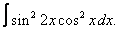117.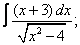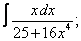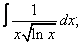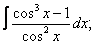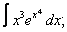
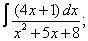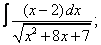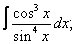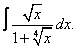118.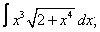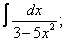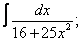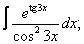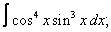
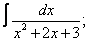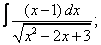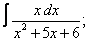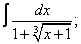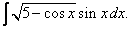119.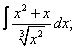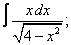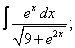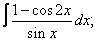
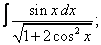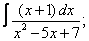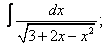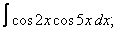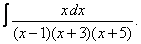220.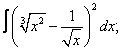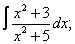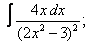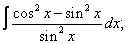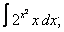
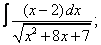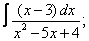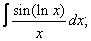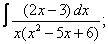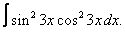221.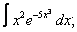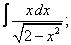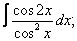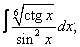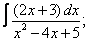
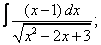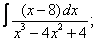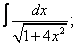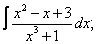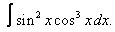222.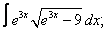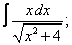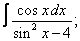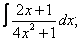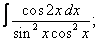
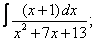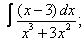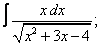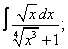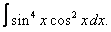223.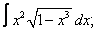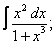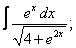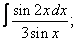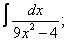
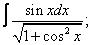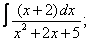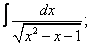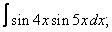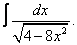224.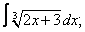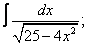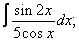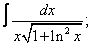
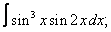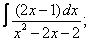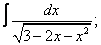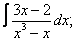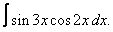225.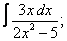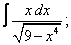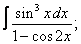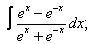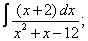

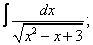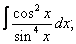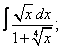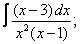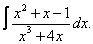Вычислите интегралы с помощью интегрирования по частям:

1. 1 а) 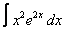;	б)	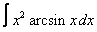2. 14 а) 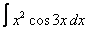;	б)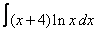
3. 2 а) 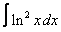;	б)	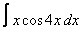4. 15 а) 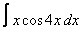;	б)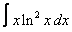
5. 3 а) 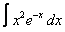;	б)	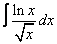6. 16 а) 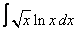;	б)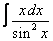
7. 4 а) 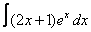;	б)	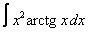8. 17 а) 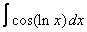;	б)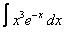
9. 5 а) 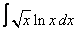;	б)	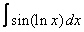10. 18 а) 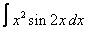;	б)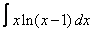
11. 6 а) 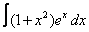;	б)	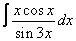12. 19 а) ;	б)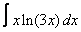
13. 7 а) 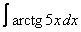;	б)	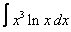14. 20 а) 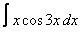;	б)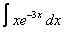
15. 8 а) 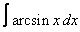;	б)	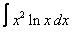16. 21 а) 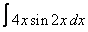;	б)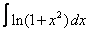
17. 9 а) 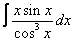;	б)	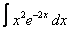18. 22 а) 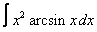;	б)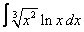
19. 10 а) 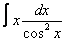;	б)	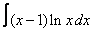20. 23 а) 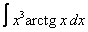;	б)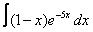
21. 11 а) 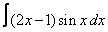;	б)	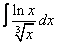22. 24 а) 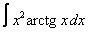;	б)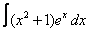
23. 12 а) 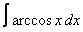;	б)	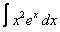24. 25 а) 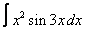;	б)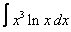
25. 13а) 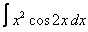;	б)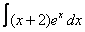

Вычислите определённые интегралы:

1. ; ; ; ; .

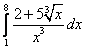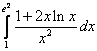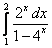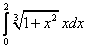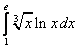2. ; ; ; ; .

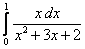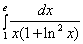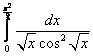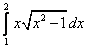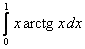3. ; ; ; ; .

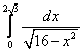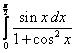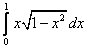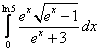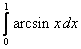4. ; ; ; ; .

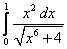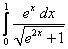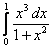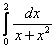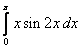5. ; ; ; ; .

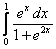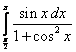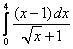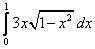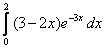6. ; ; ; ; .

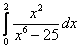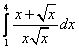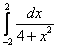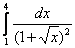7. ; ; ; ; .

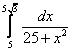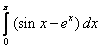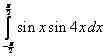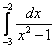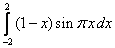8. ; ; ; ; .

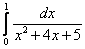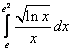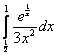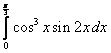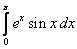9. ; ; ; ; .

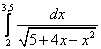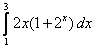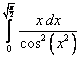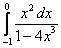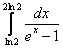10. ; ; ; ; .

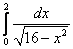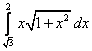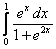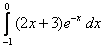11. ; ; ; ; .

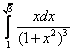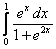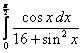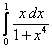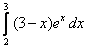12. ; ; ; ; .

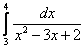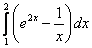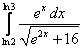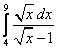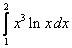13. ; ; ; ; .

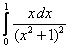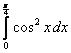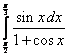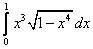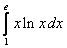14. ; ; ; ; .

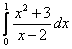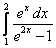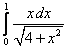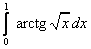15. ; ; ; ; .

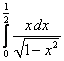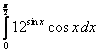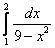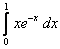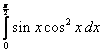16. ; ; ; ; .

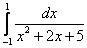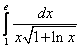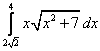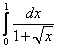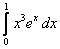17. ; ; ; ; .

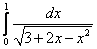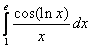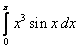18. ; ; ; ; .

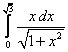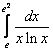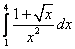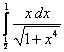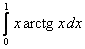19. ; ; ; ; .

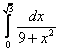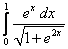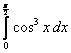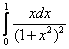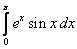20. ; ; ; ; .

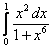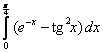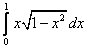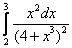21. . ; ; ; ; .

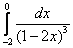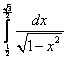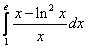22. ; ; ; ; .

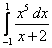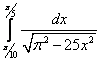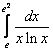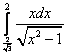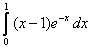23. ; ; ; ; .

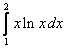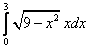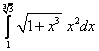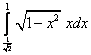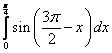24. ; ; ; ; .

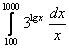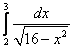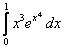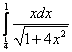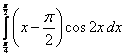25. ; ; ; ; .

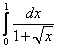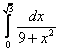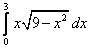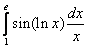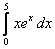Вычислите площадь фигуры, ограниченной параболами:

1. ;

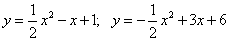2. ;

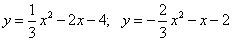3. ;

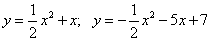4. ;

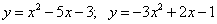5. ;

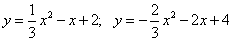6. ;

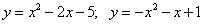7. ;

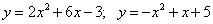8. ;

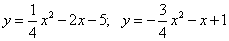9. ;

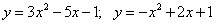10. ;

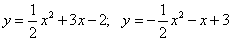11. ;

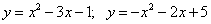12. ;

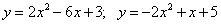13. ;

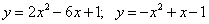14. ;

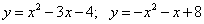15. ;

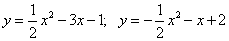16. ;

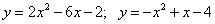17. ;

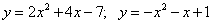18. ;

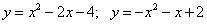19. ;

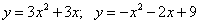20. ;

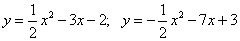21. ;

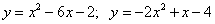22. ;

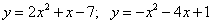23. ;

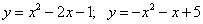24. ;

.

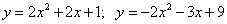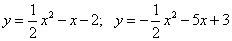Методические указания к выполнению контрольной работы № 3.

Тема: Непосредственное интегрирование

Для успешного усвоения темы необходимо знать таблицу основных интегралов:

Таблица основных интегралов

Степенные функции.

1.

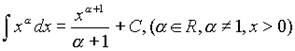
2. .

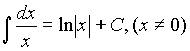Показательные функции.

3.

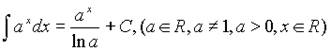
4.

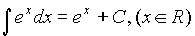
Тригонометрические функции.

5.

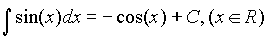
6.

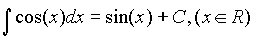
7.

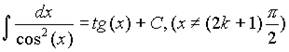
8.

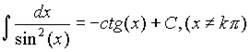
Дробно-рациональные функции.

9.

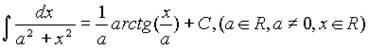
10.

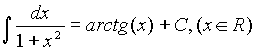
11.

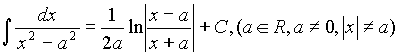
12.

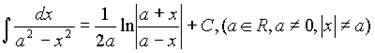
Иррациональные функции.

13.

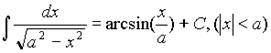
14.

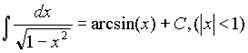
15.

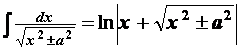
Занятие №1.

Примеры старайтесь решать самостоятельно!

Пример 1. Найти неопределенный интеграл .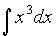

Решение.

Применяем формулу (1) , где .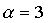

Получаем: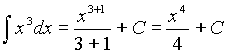

Пример 2. Найти интеграл .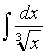

Решение.

Подынтегральная функция - это дробь 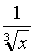. Запишем ее в виде степенной функции, а именно, 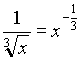. Затем используем формулу (1), при 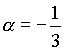. Получаем: .

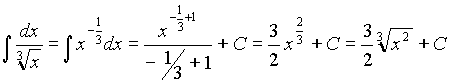Пример 3. Найти интеграл .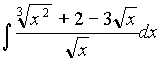

Решение.

В подынтегральной функции разделим почленно числитель на знаменатель. Затем воспользуемся неопределенного интеграла, а также формулой (1), преобразовав предварительно , если нужно подынтегральную функцию к виду 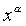. Получаем: