Зара жай сандар және олардың қасиеттері
4-анықтама. Егер 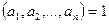 болса, онда
болса, онда 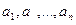 сандары өзара жай сандар деп аталады.
сандары өзара жай сандар деп аталады.
Мысалы, 17 мен 23 сандары өзара жай сандар, себебі 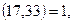 ал 30-бен 72 сандары өзара жай сандар емес, себебі
ал 30-бен 72 сандары өзара жай сандар емес, себебі 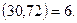
6-теорема. а және b сандары өз ара жай болуы үшін,
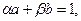 (3)
(3)
теңдігі орындалатын, 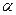 және
және 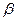 бүтін сандарының бар болуы қажетті және жеткілікті.
бүтін сандарының бар болуы қажетті және жеткілікті.
Дәлелдеуі. Қажеттігі. Егер а мен b өзара жай болса, онда 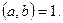 5-ші теорема бойынша,
5-ші теорема бойынша, 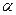 және
және 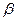 бүтін сандары табылып,
бүтін сандары табылып, 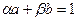 теңдігі орындалады.
теңдігі орындалады.
Жеткіліктігі. (3) теңдік орындалатындай 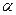 және
және 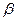 бүтін сандары бар болсын және
бүтін сандары бар болсын және 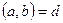 дейік. Онда, бөлінгіштіктің қасиеті бойынша (3) теңдіктен 1 саны d санына қалдықсыз бөлінеді:
дейік. Онда, бөлінгіштіктің қасиеті бойынша (3) теңдіктен 1 саны d санына қалдықсыз бөлінеді: 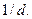 Демек
Демек 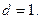 Олай болса, а мен b өз ара жай сандар.
Олай болса, а мен b өз ара жай сандар.
Салдар. Егер а мен b өз ара жай сандар болып, ал 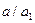 және
және 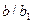 болса, онда а1 мен b1 де өз ара жай сандар. Шынында да,
болса, онда а1 мен b1 де өз ара жай сандар. Шынында да, 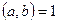 болғандықтан
болғандықтан 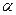 және
және 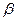 бүтін сандары табылып,
бүтін сандары табылып, 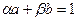 теңдігі орындалады. Ал
теңдігі орындалады. Ал 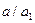 және
және 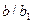 болғандықтан
болғандықтан 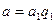 және
және 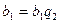 болады. Сондықтан,
болады. Сондықтан, 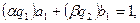 яғни
яғни 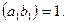
7-теорема. а және b сандарын 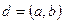 санына бөлгендегі ес еліктері өз ара жай сандар болады.
санына бөлгендегі ес еліктері өз ара жай сандар болады.
Дәлелдеуі. 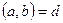 ,болса, онда
,болса, онда 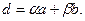 Осы теңдіктің екі жағында d-ға бөлсек.
Осы теңдіктің екі жағында d-ға бөлсек.
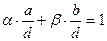 теңдігін аламыз. Бұдан, 6-шы теорема бойынша.
теңдігін аламыз. Бұдан, 6-шы теорема бойынша.
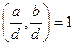 болады.
болады.
8-теорема. Егер а және  сандарының
сандарының 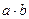 көбейтіндісі с санына бөлінсе және
көбейтіндісі с санына бөлінсе және 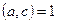 болса, онда b саны с санына бөлінеді.
болса, онда b саны с санына бөлінеді.
Дәлелдеуі. 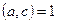 болғандықтан,
болғандықтан, 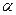 және
және 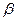 бүтін сандары табылып,
бүтін сандары табылып, 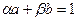 теңдігі орындалады. Осы теңдіктің екі жағында
теңдігі орындалады. Осы теңдіктің екі жағында  -ға көбейтсек
-ға көбейтсек 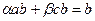 теңдігін аламыз. Теореманың шарты бойынша
теңдігін аламыз. Теореманың шарты бойынша 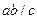 болғандықтан, бөлінгіштің қасиеті бойынша, ақырғы теңдіктің сол жағындағы қосынды да с санына бөлінеді. Онда теңдіктің оң жағындағы
болғандықтан, бөлінгіштің қасиеті бойынша, ақырғы теңдіктің сол жағындағы қосынды да с санына бөлінеді. Онда теңдіктің оң жағындағы  саны да с-ға бөлінеді, яғни
саны да с-ға бөлінеді, яғни 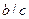 .
.
9-теорема. Егер 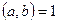 болса, онда с саны
болса, онда с саны 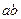 санына, сол жағдайда, тек қана сол жағдайда бөлінеді, егер с саны а-ға да
санына, сол жағдайда, тек қана сол жағдайда бөлінеді, егер с саны а-ға да  -ға да бөлінсе.
-ға да бөлінсе.
Қажеттілігі. с саны 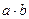 санына, ал
санына, ал 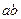 саны а және b сандарына бөлінетін болғандықтан, с саны а-ға да
саны а және b сандарына бөлінетін болғандықтан, с саны а-ға да  -ға бөлінеді.
-ға бөлінеді.
Жеткіліктігі.Егер с/а болса, онда 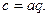 Ал с/ b және
Ал с/ b және 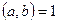 болғандықтан (8-ші теорема) q саны
болғандықтан (8-ші теорема) q саны  -ға бөлінеді. Онда
-ға бөлінеді. Онда 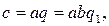 яғни с саны а-ға да b-ға бөлінеді.
яғни с саны а-ға да b-ға бөлінеді.
Мысалы, кез келген N саны 30 санына бөліну үшін, ол сан 2-ге, 3-ке, 5-ке бөліну керек. Өйткені 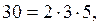 ал
ал 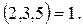
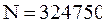 саны соңғы цифры ноль болғандықтан екі мен беске бөлінеді және цифрларының қосындысы 3-ке бөлінетіндіктен 3 саны да бөлінеді. Демек, 324750 саны 30-ға бөлінеді.
саны соңғы цифры ноль болғандықтан екі мен беске бөлінеді және цифрларының қосындысы 3-ке бөлінетіндіктен 3 саны да бөлінеді. Демек, 324750 саны 30-ға бөлінеді.
10-теорема. Егер 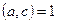 және
және 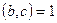 болса, онда
болса, онда 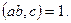
Дәлелдеуі. Теорема тұжырымына кері, 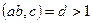 дейік. Онда
дейік. Онда 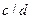 болады. Теорема шарты бойынша
болады. Теорема шарты бойынша 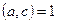 болғандықтан, 6-теореманың салдары бойынша,
болғандықтан, 6-теореманың салдары бойынша, 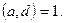 Ал
Ал 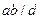 және
және 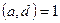 болғандықтан, 8-теорема бойынша,
болғандықтан, 8-теорема бойынша, 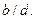 Демек
Демек 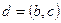 екендігі шығады. Бұл теорема шартына қайшы. Бұдан
екендігі шығады. Бұл теорема шартына қайшы. Бұдан 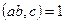 екендігі шығады. Бұл теореманы төмендегіше жалпылауымызға болады. Егер
екендігі шығады. Бұл теореманы төмендегіше жалпылауымызға болады. Егер 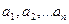 сандары
сандары 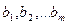 сандарының әрқайсысымен өз ара жай болса, онда
сандарының әрқайсысымен өз ара жай болса, онда 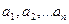 көбейтіндісі
көбейтіндісі 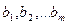 көбейтіндісімен өз ара жай болады.
көбейтіндісімен өз ара жай болады.
Салдар. Егер 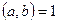 болса, онда кез келген
болса, онда кез келген 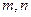 натурал сандар үшін
натурал сандар үшін 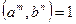 болады. Ескерту.
болады. Ескерту. 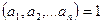 дегеннен
дегеннен 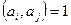 шықпайды, мұнда
шықпайды, мұнда 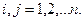
5-анықтама. Егер 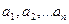 сандарының кез келген екеуі өз ара жай болса, онда бұл сандар қос-қостан өз ара жай деп аталады.
сандарының кез келген екеуі өз ара жай болса, онда бұл сандар қос-қостан өз ара жай деп аталады.
Мысалы, 715, 96, 119 сандары қос-қостан өз ара жай, өйткені