Способ плоскопараллельного перемещения.

ПЛАН

1. Основные сведения о преобразовании плоскостей.

2. Способ замены плоскостей проекций. Проецирование на дополнительную плоскость проекций (замена плоскостей проекций). Построение дополнительных проекций точки и прямой. Преобразование прямой общего положения в прямую частного положения (уровня и проецирующую). Преобразование плоскости общего положения в плоскость частного положения (проецирующую и уровня).

3. Способ вращения. Вращение вокруг проецирующей прямой. Вращение точки, прямой, плоскости. Вращение вокруг линий уровня. Вращение вокруг горизонтали и фронтали, вращение вокруг следа плоскости, совмещение.

4.Способ плоскопараллельного перемещения.

СОДЕРЖАНИЕ

1. Основные сведения о преобразовании плоскостей.

Исходный чертеж может быть неудобен для определения и изучения тех или иных метрических или позиционных свойств, присущих предмету в натуре. В этих случаях чертеж преобразуют так, чтобы чертеж позволил получить нужное решение без сложных геометрических построений.

Задачи начертательной геометрии можно разделить на позиционные и метрические.

В позиционных задачах требуется найти положение геометрических фигур (точка, прямая, плоскость, тело) удовлетворяющих условия задач.

В метрических задачах требуется найти натуральные размеры геометрических фигур.

При решении метрических задач пользуются преимущественно 2-мя способами преобразованием проекций. Способом замены плоскостей проекции и способом вращения.

В 1-ом способе положения фигуры относительно плоскостей проекции остается неизменным, изменяется только положение одной из плоскостей. Причем заменяемая плоскость в положении перпендикулярном к плоскости.

Во 2-ом способе положение плоскости проекций остается неизменным изменяется положение фигуры относительно плоскостей проекции, путем вращения плоскости проекций вокруг оси, параллельной одной из плоскостей проекции.

Основные задачи.

1) Прямую общего положения, преобразовать прямую параллельную одной из плоскостей проекции, т.е. найти натуральную величину прямой.

2) Прямую, параллельную одной из плоскостей проекций, преобразовать в проецирующую, т.е. поставить в положение перпендикулярно плоскости проекции, чтобы прямая спроецировалась в точку.

3) Плоскость общего положения преобразовать в проецирующую к одной из плоскостей проекций. Чтобы получить проецирующую плоскость, то в плоскости проводят горизонталь и ставят перпендикулярно к плоскости проекций.

4) Преобразовать плоскость из плоскости проецирующей в плоскость уровня параллельную одной из плоскостей проекции, т.е. найти натуральную величину в плоскости. Чтобы получить плоскость уровня, которая параллельна одной из плоскостей проекции (найти натуральную величину) необходимо поставить ее параллельно плоскости проекций.

Способ замены плоскостей проекций. Проецирование на дополнительную плоскость проекций (замена плоскостей проекций). Построение дополнительных проекций точки и прямой. Преобразование прямой общего положения в прямую частного положения (уровня и проецирующую). Преобразование плоскости общего положения в плоскость частного положения (проецирующую и уровня).

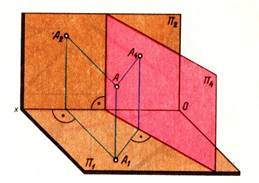При проецировании предмета на дополнительную плоскость проекций предмет не меняет своего положения в пространстве по отношению к плоскостям проекций, а исходная система основных плоскостей проекций дополняется новыми, более удобными, для решения задачи.

Принципы построения дополнительной проекции точки на одну дополнительную плоскость проекций заключается в том, что в систему перпендикулярных друг другу плоскостей проекций F и H вводится плоскость перпендикулярная одной из плоскостей проекций. При построении эпюра дополнительная плоскость (F₁ или H₁) проекций совмещается с той основной плоскостью проекций, к которой она была перпендикулярна. На эпюре появляется еще одна линия проекционной связи, перпендикулярная новой оси проекций (х₁), а расстояние от оси до новой проекции точки равно расстоянию от точки в пространстве до той плоскости к которой дополнительная плоскость проекций не была введена.

Построение дополнительных проекций прямой основано на построении дополнительных проекций точки: на прямой выделяем две произвольные точки и строим их дополнительные проекции. Если необходимо преобразовать прямую общего положения в прямую уровня, то новая плоскость проекций вводится параллельно прямой. Если необходимо преобразовать прямую общего положения в проецирующую прямую, то ее сначала преобразуют в прямую уровня, а затем в проецирующую, путем введения новой плоскости проекций перпендикулярно прямой уровня.

Чтобы плоскость общего положения преобразовать в проецирующую, необходимо новую плоскость проекций расположить перпендикулярно к линии уровня. Чтобы плоскость общего положения преобразовать в плоскость уровня, необходимо сначала преобразовать ее в проецирующую, а затем ввести параллельно ей новую плоскость проекций, в результате этого преобразования получится плоскость уровня.

Основные типы задач:

1. Прямую общего положения преобразовать в прямую, параллельную одной из плоскостей проекций, т.е. найти натуральную величину прямой.

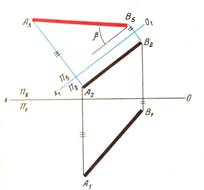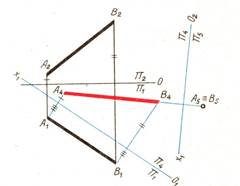2. Прямую АВ, параллельную одной из плоскостей проекций, преобразовать в проецирующую, т.е. поставить в положение, перпендикулярное плоскости проекций, чтобы прямая спроецировалась в точку.

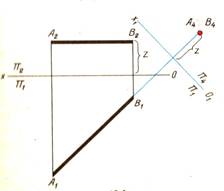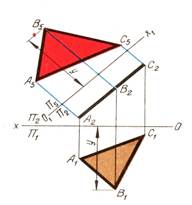
3. Плоскость общего положения преобразовать в проецирующую.

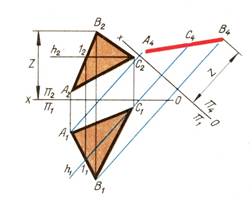
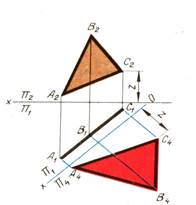
4. Преобразовать плоскость из плоскости проецирующей в плоскость уровня, параллельную одной из плоскостей проекций, т.е. найти натуральный размер плоскости.

1. Способ вращения. Вращение вокруг проецирующей прямой. Вращение точки, прямой, плоскости. Вращение вокруг линий уровня. Вращение вокруг горизонтали и фронтали, вращение вокруг следа плоскости, совмещение.

Вращением фигуры вокруг оси называется такое движение, при котором каждая точка фигуры перемещается по окружности, плоскость которой перпендикулярна к оси вращения, центр расположен в точке пересечения оси вращения с плоскостью вращения, а радиус равен расстоянию от точки до оси вращения.

Пусть точка вращается вокруг оси. Вращение можно производить как по часовой стрелке, так и против нее. Остановим вращение в тот момент, когда она повернется на некоторый угол и займет новое, преобразованное положение.

При вращении прямой вокруг оси перпендикулярной к плоскости проекций и проходящей через крайнюю точку отрезка прямой, расстояние между проекциями точек на данной плоскости проекции не изменяется. Если поставить прямую перпендикулярно или параллельно плоскости проекций, при проведении операции вращения, то она станет соответственно в проецирующей или линией уровня.

При вращении плоскости вокруг оси перпендикулярной к плоскости проекций и проходящей через точку пересечения прямых, ограничивающих плоскость, расстояние между проекциями точек на данной плоскости проекций не изменяется.

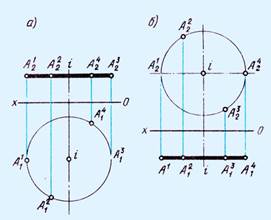Основные задачи

1. Нахождение натуральной величины отрезка.

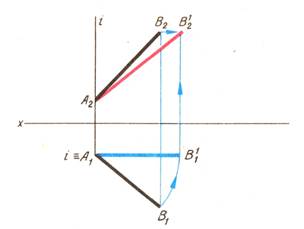2. Нахождение натуральной величины плоской фигуры частного положения.

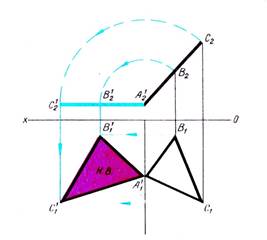Способ совмещения

Этот способ частный случай способа вращения, когда осью вращения служит линия пересечения данной плоскости с одной из плоскостей проекции или одна из главных линий горизонталь или фронталь плоскости.

Основные задачи

1. Пример совмещения прямой линии с горизонтальной плоскостью проекций.

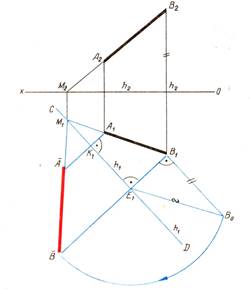2. Совмещение плоской фигуры частного положения с одной из плоскостей проекций.

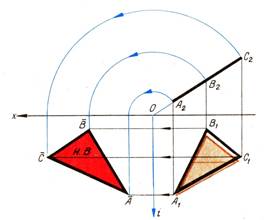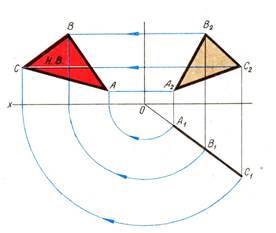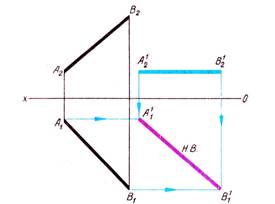
Способ плоскопараллельного перемещения.

Рассмотрим суть способа плоскопараллельного перемещения на примере движения отрезка. При плоскопараллельном перемещении фигуры относительно плоскости проекций Н фронтальные проекции ее точек перемещаются по прямым, параллельным оси проекций, а горизонтальная проекция фигуры остается конгруэнтной самой себе.