Сильные разрывы в магнитной гидродинамике.

Сильными разрывами называются такие поверхности, на которых рвутся искомые магнитогазодинамические параметры. Для того, чтобы вывести соотношения на таких разрывах, необходимо записать законы сохранения в интегральной форме. В Лекции 2эти законы были выписаны в общем случае, в котором учитываются все диссипативные процессы (вязкость, теплопроводность, джоулевы потери вследствие выделения тепла при протекании электрических токов). Поверхности сильного разрыва являются идеализацией, в которой эти процессы не учитываются. В природе эти процессы приводят к образованию тонких областей, в которых параметры газа изменяются непрерывно. Малая толщина этих областей и приводит к упомянутой выше идеализации. Поэтому ниже мы будем рассматривать поверхности сильного разрыва в рамках идеальной магнитной гидродинамики.

Тогда законы сохранения массы, импульса и энергии в интегральной форме будут, соответственно, иметь вид

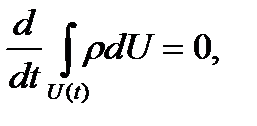
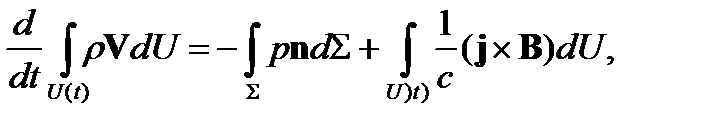
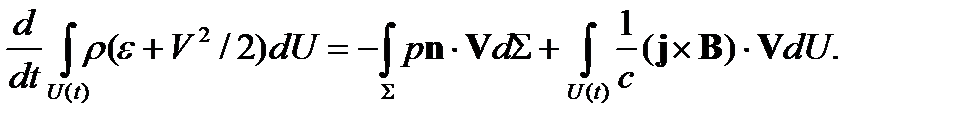
Воспользовавшись формулой для производной от интеграла по движущемуся объему и предположив, что течение стационарно (система координат связана с поверхностью сильного разрыва), из последних уравнений получим

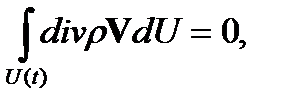
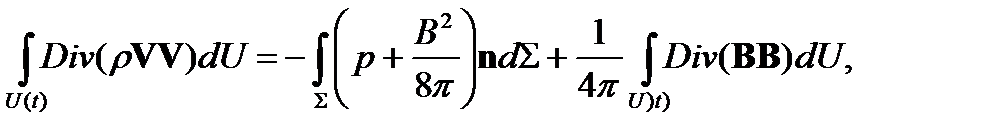
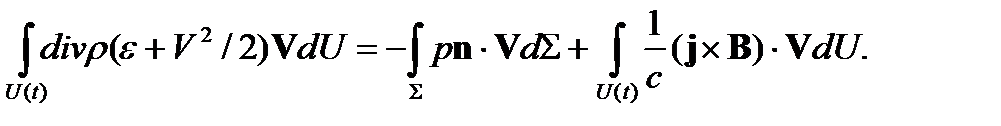
При получении дифференциальных уравнений магнитной гидродинамики было предположено, что подынтегральные функции непрерывны, а переход от интегралов по поверхности к интегралам по объему позволил получить эти уравнения. Уравнения, выписанные выше, справедливы и для разрывных функций. Чтобы получить соотношения на сильных разрывах, перейдем в последних уравнениях от интегралов по объему к интегралам по поверхности ∑. Для уравнения неразрывности получим

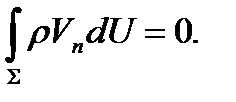
Если разность подынтегральных функций с двух сторон от поверхности сильного разрыва ∑ обозначить через фигурные скобки, как это мы делали для слабых разрывов, то из последнего уравнения получим закон сохранения массы

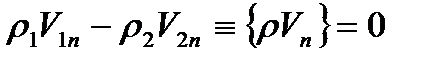(1)

Закон сохранения импульса в интегральной форме будет иметь вид

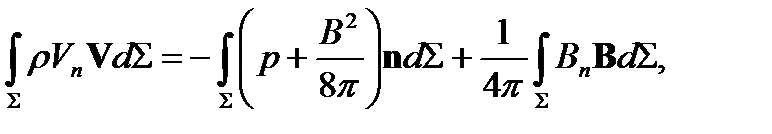
а для разрывов в проекции на нормаль и касательную к поверхности ∑

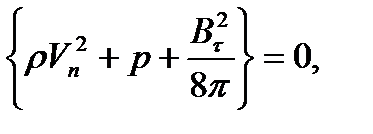(2)

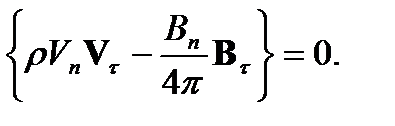(3)

В (2) и (3) учтено, что [B_n]=0. Выпишем теперь закон сохранения энергии

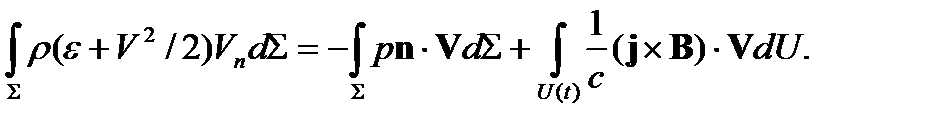(4)

Сделаем некоторые преобразования в последнем члене этого уравнения. Имеем

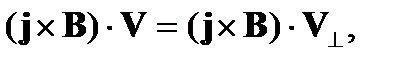
где справа - вектор скорости в направлении, нормальном вектору индукции магнитного поля. Очевидно, что уравнение индукции магнитного поля в идеальной магнитной гидродинамике предполагает, что

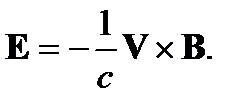(5)

Действительно, взяв операцию rotот этого равенства и воспользовавшись одним из уравнений Максвелла, получим уравнение (11) Лекции 4. Выразим теперь VчерезВиз (5). Получим

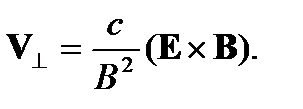
Подставив это выражение в последний член (4), воспользовавшись уравнениями Максвелла для стационарного случая и векторными тождествами

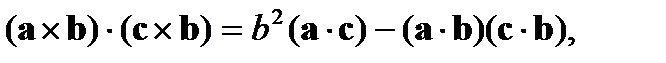
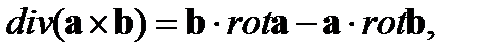
получим

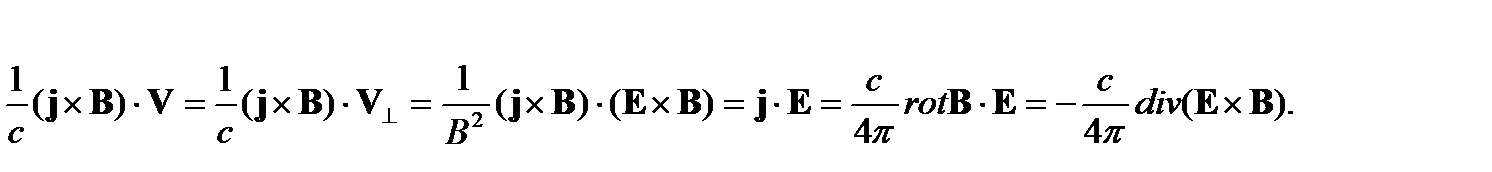
Подставляя это выражение в последний член (4) и переходя от объемного интеграла к интегралу по поверхности, будем иметь

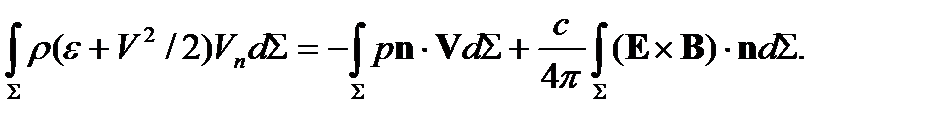
Тогда закон сохранения энергии на поверхности сильного разрыва будет иметь вид

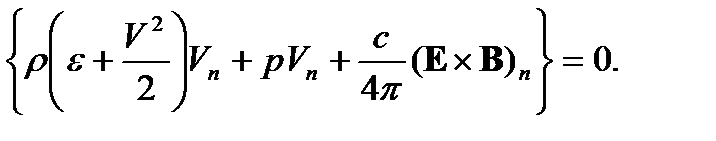(6)

В электродинамике последнему члену в (6) придают смысл плотности потока электромагнитной энергии (вектор Умова-Пойнтинга). Прежде, чем перейти к классификации поверхностей сильного разрыва, несколько преобразуем этот член, используя (5).

.

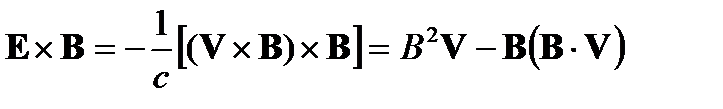Этот вектор в проекции на нормаль к поверхности разрыва будет иметь вид

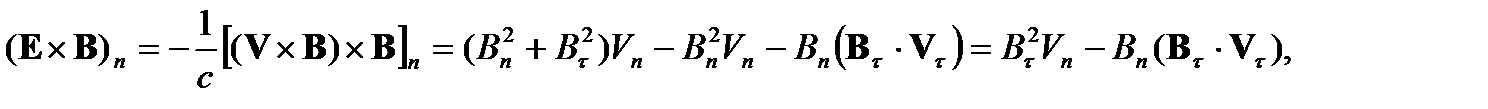
где индекс «τ» означает проекцию вектора на касательную к поверхности разрыва. Подставив последнее выражение в (6), окончательно закон сохранения энергии на поверхности сильного разрыва будет иметь вид

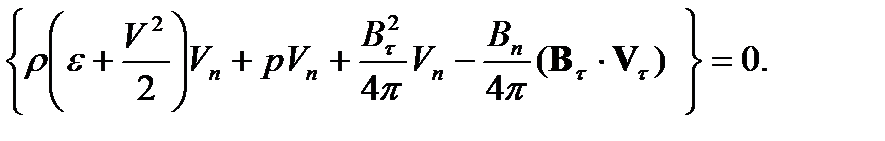(7)

Необходимо еще добавить непрерывность касательной составляющей электрического поля, которое следует из rot E=0, и равенства (5)

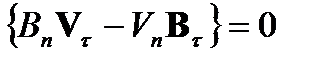, (8)

а также непрерывность нормальной компоненты магнитного поля

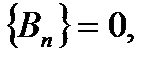(9)

которое следует из divB= 0.

Таким образом, мы получили систему уравнений (1) - (3), (7) – (9), которая определяет изменение параметров при пересечении поверхности сильного разрыва.

Лекция 915.11.16

Классификация поверхностей сильного разрыва.

Введем обозначение m= ρV_n для потока массы через поверхность разрыва. Классификация сильных разрывов зависит от наличия через них потока массы. Рассмотрим сначала первый случай, когда поток массы отсутствует, т.е.

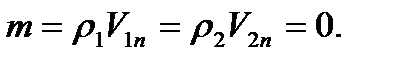(1)

Очевидно, что в этом случае нормальная компонента скорости равна нулю. Тогда из закона сохранения импульса в проекции на нормаль (соотношение (2) прошлой лекции) получим

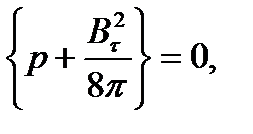(2)

а из проекции на касательную (соотношение (3) прошлой лекции) будем иметь

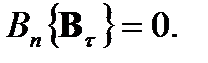(3)

Непрерывность касательной составляющей электрического поля дает (соотношение (8) прошлой лекции)

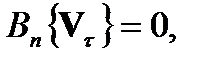(4)

а из закона сохранения энергии будем иметь

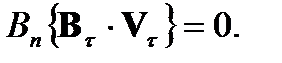(5)

Последние соотношения получены при учете непрерывности нормальной компоненты магнитного поля. Таким образом, случай отсутствия потока массы через поверхность сильного разрыва сводится к анализу соотношений (2) – (5). Рассмотрим два возможных варианта.

а) Нормальная компонента магнитного поля равна нулю, т.е. B_n= 0.

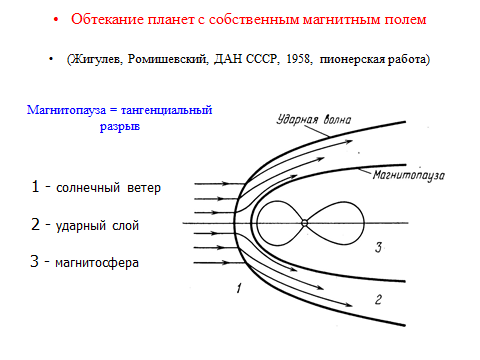Скорость и магнитное поле параллельны в этом случае поверхности сильного разрыва. При этом, как видно из (3) - (5), касательные составляющие скорости и магнитного поля могут иметь произвольный разрыв, а гидростатическое давление на разрыве связано соотношением (2) с магнитным давлением. При этом, суммарное давление должно быть непрерывным. Поскольку плотность может в этом случае иметь произвольный разрыв, как видно из (1), то все термодинамические функции могут иметь произвольный разрыв. Такая поверхность сильного разрыва называется тангенциальным разрывом.

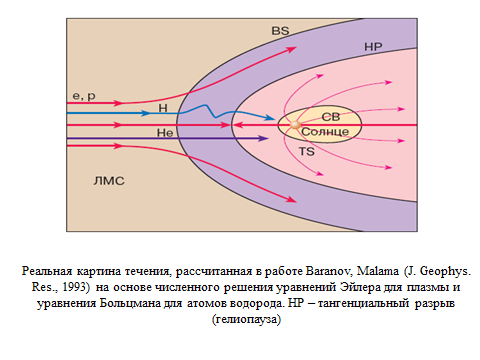Такая поверхность разрыва есть поверхность раздела двух жидкостей с разными термодинамическими параметрами, которые движутся друг относительно друга. В обычной гидродинамике типичным примером тангенциального разрыва является поверхность, разделяющая водное пространство (например, океан или река) и воздушное. В магнитной гидродинамике в качестве тангенциального разрыва можно привести поверхность раздела между солнечным ветром и магнитосферой Земли (в геофизике такая поверхность называется магнитопаузой) или между солнечным ветром и межзвездной средой (гелиопауза).

б) Нормальная компонента магнитного поля не равна нулю, т.е. B_n≠ 0.

В этом случае, как видно из (3) - (5), скорость и магнитное поле непрерывны. Из (2) тогда следует, что и гидростатическое давление непрерывно. Остальные термодинамические параметры (плотность, температура, внутренняя энергия) могут иметь произвольный разрыв. Такой разрыв называется контактным разрывом.Такому разрыву нет аналога в обычной гидродинамике, хотя часто в отсутствие магнитного поля тангенциальный разрыв называют контактным (например, в ударных трубах, где нет тангенциальной составляющей скорости).