Выбор расчетных функций с учетом условий закрепления панелей

Панели, нагруженные растягивающими силами. На рис. 3.2 показаны варианты возможного нагружения свободного края панели, которые вызовут чистое растяжение. Если действующие вдоль оси 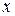нагрузки создают кроме растяжения и изгибающий момент, т.е. приложены эксцентрично, то решение необходимо разбить на две задачи - симметричную и кососимметричную.

Изучим вопрос выбора аппроксимирующих функций, входящих в уравнения (3.10) и (3.11), при растяжении панели. При решении задачи, прежде всего, задаются функции, соответствующие гипотезе Бернулли. Эти функции следует дополнить функциями депланации, т.е. функциями, уточняющими балочные функции, которые позволяют удовлетворить граничные условия. С помощью таких функций можно, например, удовлетворить статические граничные условия при точечном закреплении панели. Пример задания функций при растяжении панели показан на рис. 3.3.

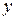Функция отвечает продольному перемещению поперечного сечения панели как жесткого целого. Остальные функции учитывают депланацию сечения с учетом геометрических условий точечного закрепления по координате и отвечают смыслу задачи. Например, первичные функции и для задачи растяжения можно выбирать в тригонометрическом или полиномиальном видах: ; или ; и т.д. и или ;

Рис. 3.2. Нагружение панели

Рис. 3.3. Вид выбранных функций при растяжении

а также ; или ; ; и т.д. Эти функции удовлетворяют геометрическим граничным условиям, отвечают условиям и виду приложенных нагрузок и характеру возможных перемещений, т.е. функция учитывает, что перемещения постоянны в сечении и в пластине, и в продольных подкрепляющих элементах. Функция учитывает линейное перемещение 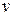в сечении панели по координате 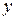, т.е. деформируемость сечения по координате 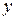. Остальные начальные функции учитывают, кроме того, что в точках при перемещения в точках крепления и .

Панели, нагруженные поперечными силами. Вторая задача есть задача поперечного изгиба панели. Здесь функции и относительно первой задачи (см. риc. 3.4, 3.5) меняются местами, так как при изгибе панели продольные перемещения кососимметричны, а для поперечных – симметричны. В этом случае балочные функции определяют поворот поперечного сечения функцией и вертикальное смещение вдоль оси 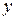функцией . Остальные функции учитывают депланацию сечения с учетом геометрических условий точечного закрепления по координате 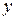и отвечают смыслу задачи. Например, начальные первообразные функции и для задачи изгиба можно выбирать в тригонометрическом или

Рис. 3.4. Вид выбранных функций при изгибе

полиномиальном видах: ; или ; и т.д. и ; или ; и т.д. Здесь можно принять, что функция учитывает только продольное перемещение в подкрепляющих элементах при значении , а функция справедлива для всего сечения, включая и продольные элементы.