Решение волнового уравнения в случае неоднородной среды
 (Ф19.1)
(Ф19.1)
Рассматриваем нормальные волны, т.е. источников нет.
 , где
, где 
Будем предполагать 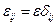 . Здесь
. Здесь  , если
, если  .
.
Запишем ещё одно уравнение для среды сравнения, которая имеет однородные диэлектрические свойства, и геометрически идентичная нашей неоднородной рассматриваемой среде.
 (Ф19.2)
(Ф19.2)
 , где
, где 
Это уравнение решать проще чем, чем исходное. Будем обозначать через  выражения вида:
выражения вида:

Вычитая из (Ф19.1) – (Ф19.2) получим:

Введем обозначение  , тогда:
, тогда:

в компонентной форме:

Используем функцию Грина для оператора 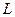 , тогда:
, тогда:


или

Оператор  . Обозначим
. Обозначим  , тогда:
, тогда:

 - интегральный оператор, действующий на поле
- интегральный оператор, действующий на поле 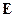 .
.
Это уравнение решается методом последовательного приближения:
0-е приближение 
1-е приближение 
…
(n+1)-е приближение 
Полученные результаты представляются в виде ряда Неймана (если этот ряд сходится):

Условие сходимости ряда Неймана - 
§ 20. Расчет показателя рассеяния 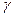 , фазовой
, фазовой 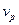 и групповой
и групповой 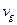 скорости электромагнитных волн в неоднородных средах
скорости электромагнитных волн в неоднородных средах
При распространении волн в неоднородных средах наибольший интерес представляет среднее поле – когерентная составляющая  . Оказывается, что поле
. Оказывается, что поле  удовлетворяет уравнению:
удовлетворяет уравнению:
 ,
,
где  - эффективный интегро-дифференциальный оператор.
- эффективный интегро-дифференциальный оператор.

Важное значение имеет фурье-образ оператора  , т.е. тензор
, т.е. тензор
 , где
, где 
 - определяет свойства когерентной составляющей волны. Когерентная составляющая волны:
- определяет свойства когерентной составляющей волны. Когерентная составляющая волны:

Вектор  определяется из решения дисперсионного уравнения:
определяется из решения дисперсионного уравнения:

Откуда получаем  . Мнимая часть
. Мнимая часть  определяет рассеяние электромагнитных волн на неоднородностях среды.
определяет рассеяние электромагнитных волн на неоднородностях среды.
Тогда показатель рассеяния  , фазовая скорость
, фазовая скорость  и групповая скорость
и групповая скорость  .
.
§ 21. Асимптотические выражения для показателя рассеяния 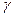
Рассмотрим  . Если
. Если  , то
, то  и
и  .
.
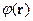 - описывает характер убывания взаимодействия между неоднородностями. Для описания
- описывает характер убывания взаимодействия между неоднородностями. Для описания 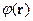 вводится параметр
вводится параметр 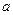 :
:

Это для случая статистически однородной и изотропной среды (т.е. микросреда неоднородная, а макросреда – однородная). Здесь 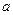 - масштаб корреляции, т.е. расстояние на котором взаимодействие между неоднородностями убывает в е раз.
- масштаб корреляции, т.е. расстояние на котором взаимодействие между неоднородностями убывает в е раз.
Удобно ввести безразмерный коэффициент:

 имеет различную зависимость от волнового числа в зависимости от диапазона длин волн.
имеет различную зависимость от волнового числа в зависимости от диапазона длин волн.
Рассмотрим диапазон длинных волн 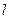 . Релей получил
. Релей получил  , где
, где 
Здесь  , т.е. длинноволновая асимптотика.
, т.е. длинноволновая асимптотика.
Рассмотрим случай коротких волн 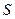 . Здесь
. Здесь  , где вводится ограничение
, где вводится ограничение  ,
,  .
.
 , т.е.
, т.е.  (случай коротких волн)
(случай коротких волн)
 , т.е.
, т.е. 
Мы получили выделенный интервал длин волн, для которого:

т.е. длины волн малы по сравнению с 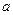 и большие по сравнению с
и большие по сравнению с  .
.
Рассмотрим ультракоротких волн  . Здесь
. Здесь  и
и 
Графически все три случая можно изобразить следующим образом:
 Ширина
Ширина 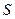 -области определяется величиной
-области определяется величиной  . С ростом
. С ростом  область
область 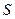 уменьшается. С дальнейшим ростом
уменьшается. С дальнейшим ростом  может исчезнуть область
может исчезнуть область  - область ультракоротких волн.
- область ультракоротких волн.
