Задача о кратчайшем пути
Задача о кратчайшем пути состоит в нахождении связанных между собой дорог на транспортной сети, которые в совокупности имеют минимальную длину от исходного пункта до пункта назначения.
Алгоритм для сетей без циклов.
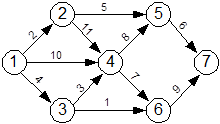
Рис.6
Пусть имеется цепь рис.6 Необходимо найти кратчайший маршрут между пунктами 1 и 7. Введем следующие обозначения: 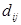 – расстояние между i-ым и j-ым узлами;
– расстояние между i-ым и j-ым узлами; 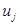 – кратчайшее расстояние от узла 1 до j-го узла.
– кратчайшее расстояние от узла 1 до j-го узла.
Общая формула для вычисления 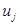 имеет вид
имеет вид
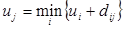
Решение для графа рис.6:
Очевидно, что 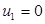 .
.
Для узлов 2 и 3 получим: 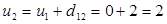 ;
;
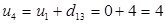 .
.
Узел 4: 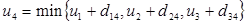 =
= 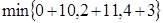 = 7.
= 7.
Узлы 5 и 6: 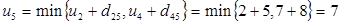 ;
;
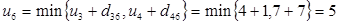 .
.
Узел 7: 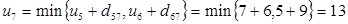 .
.
Минимально расстояние равно 13 и соответствующий маршрут 1®2®5®7.
Алгоритм для сетей с циклами.
В этом случае алгоритм несколько сложнее.
Шаг 1. Пусть 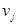 – сумма длин дуг, образующих цепь, ведущую из узла 1 в узел j. Положим
– сумма длин дуг, образующих цепь, ведущую из узла 1 в узел j. Положим 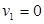 и
и 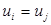 если
если 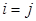 . При условии, что i и j соединены дугой, величина
. При условии, что i и j соединены дугой, величина 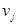 определяется как
определяется как
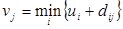 .
.
Процесс начинается с 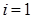 и
и 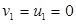 .
.
Шаг 2. Положить 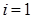 .
.
а) Вычислить 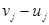 для всех j.
для всех j.
б) Если 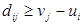 для всех j, то между узлами i и j не существует более короткого пути. Если
для всех j, то между узлами i и j не существует более короткого пути. Если 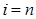 , перейти к п.(г). Иначе положить
, перейти к п.(г). Иначе положить 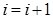 и перейти к п.(а).
и перейти к п.(а).
в) Если 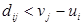 , вычислить новые значения
, вычислить новые значения 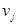 и
и 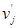 , используя формулу
, используя формулу
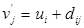 .
.
Заменить 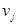 и
и 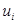 для
для 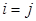 на
на 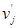 . Если
. Если 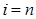 , перейти к п.(г); в противном случае положить
, перейти к п.(г); в противном случае положить 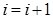 и перейти к п.(а).
и перейти к п.(а).
г) Если значение 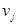 изменялось в п.(в), повторить шаг 2, используя измененное значение. В противном случае перейти к шагу 3.
изменялось в п.(в), повторить шаг 2, используя измененное значение. В противном случае перейти к шагу 3.
Шаг 3. Полученные значения 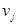 определяют кратчайшие расстояния между узлами 1 и
определяют кратчайшие расстояния между узлами 1 и 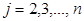 . Для получения соответствующих цепей последняя дуга
. Для получения соответствующих цепей последняя дуга 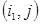 в цепи
в цепи 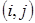 должна удовлетворять условию
должна удовлетворять условию
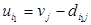 .
.
После определения 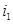 предпоследняя вершина
предпоследняя вершина 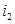 должна удовлетворять равенству
должна удовлетворять равенству
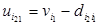 .
.
Процесс продолжается пока не будет достигнут узел 1.
Задача о максимальном потоке
Предположим, что каждая дуга сети обладает пропускными способностями в обоих направлениях, которые определяют максимальное количество потока, проходящего по заданной дуге. Ориентированная дуга соответствует нулевой пропускной способности в запрещенном направлении. Пропускные способности 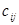 можно представить в матричной форме.
можно представить в матричной форме.
Шаг 1. Найти цепь, соединяющую s с t (источник и приемник), по которой поток принимает положительное значение в направлении 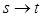 .Если такой цепи не существует, перейти к шагу 3. В противном случае перейти к шагу 2.
.Если такой цепи не существует, перейти к шагу 3. В противном случае перейти к шагу 2.
Шаг 2. Пусть 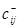 (
( 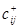 ) – пропускные способности дуг цепи
) – пропускные способности дуг цепи 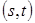 в направлении
в направлении 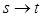 (
( 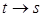 ) и
) и
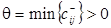 .
.
Матрицу пропускных способностей 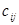 изменить следующим образом:
изменить следующим образом:
а) вычесть q из всех 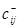 ;
;
б) прибавить q ко всем 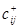 .
.
Заменить текущую матрицу 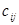 на вновь полученную и перейти к шагу 1.
на вновь полученную и перейти к шагу 1.
Шаг 3. Найти максимальный поток в сети. Пусть 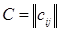 – исходная матрица пропускных способностей,
– исходная матрица пропускных способностей, 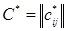 – последняя полученная в результате модификаций матрица. Оптимальный поток
– последняя полученная в результате модификаций матрица. Оптимальный поток 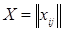 в дугах задается как
в дугах задается как
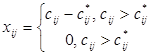 .
.
Максимальный поток из s в t равен
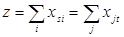 .
.
Задачи
3.1 Решите задачу о минимизации сети для графа
а) Рис.7.
б) Рис.8.
в) Рис.9.
г) Рис.10

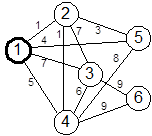
Рис.7 Рис.8 Рис.9 Рис.10
3.2 Для графа рис.6 решите задачу о нахождении кратчайшего пути.
а) От узла 1 к узлу 5.
б) От узла 1 к узлу 6.
3.3 Решите задачу о нахождении кратчайшего пути для графа:
а) Рис.11.
б) Рис.12.
в) Рис.13.
г) Рис.14.
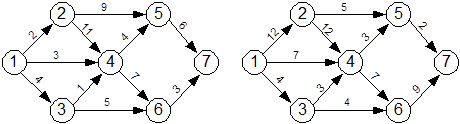
Рис.11 Рис.12
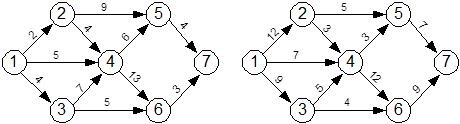
Рис.13 Рис.14
Конечные автоматы
Основные понятия
Логическая схема (автомат), значения выходных переменных которого определяется только комбинацией значений переменных на его входах в данный момент времени называется комбинационной схемой. Если состояние схемы зависит также и от предыдущих значений входных переменных, схему называют последовательностной. Оба типа схем, в которых входные и выходные переменные принимают значения из конечных алфавитов, объединяются под названием конечные автоматы.
Конечный автомат М определяется как система с конечным входным алфавитом 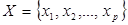 , конечным выходным алфавитом
, конечным выходным алфавитом 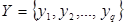 , конечным множеством состояний
, конечным множеством состояний 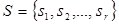 и двумя характеристическими функциями:
и двумя характеристическими функциями:
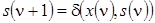 ;
;
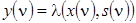 ,
,
называемых соответственно функцией переходов и функцией выходов.
Работу автомата можно представить таблицей переходов, таблицей выходов, графом автомата или матрицей соединений.
В таблице переходов:
| s(n) \ x(n) | ||||
левый столбец соответствует текущему состоянию автомата, верхняя строка – значение на входе автомата. Таблица определяет следующее состояние автомата при заданном входном воздействии и текущем состоянии автомата.
В таблице выходов:
| s(n) \ x(n) | ||||
определяется значение на выходе автомата при заданном входном воздействии и текущем состоянии автомата.
Две указанные таблицы могут быть объединены в общую таблицу переходов, где определятся состояние автомата на следующем такте и его выход:
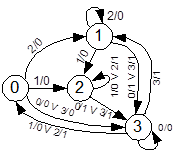 |
| s(n) \ x(n) | ||||
| 3/0 | 2/0 | 1/0 | 3/0 | |
| 3/1 | 2/0 | 1/0 | 3/1 | |
| 3/1 | 2/0 | 2/1 | 3/1 | |
| 3/0 | 0/0 | 0/1 | 1/1 |
Рис.15
Граф автомата, соответствующий приведенным таблицам представлен на рис.15. Состояния автомата представлены вершинами графа. Ребрам графа приписаны входное воздействие/выход автомата.
Матрица соединений, соответствующая автомату с графом рис.15 представлена ниже:
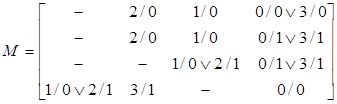 .
.
Задачи
4.1 Накопительный счетчик, на вход которого подаются двоичные цифры 0 и 1, подсчитывает по модулю 3 общее число поступивших на вход единиц. Перечислите входной и выходной алфавиты, а также определите множество состояний.
а) Запишите таблицу переходов соответствующего конечного автомата.
б) Постройте граф автомата.
в) Запишите матрицу соединения автомата.
4.2 На основании графа рис.16 определите выходную последовательность и смену состояний автомата при начальном состоянии 3 и входной последовательности:
а) (0 1 2 3 3 0 1 2);
б) (2 0 1 3 2 0 0 2);
в) (3 1 0 0 2 3 0 2 1 1);
г) (2 3 0 1 0 3 2 1 1);
д) (3 3 2 0 1 0 0 2 1).
4.3 Постройте матрицу переходов и матрицу соединений для автомата
а) Рис.17.
б) Рис.18.
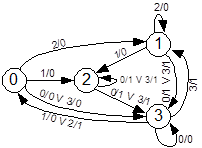
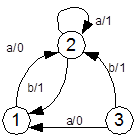
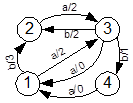
Рис.16 Рис.17 Рис.18
Теория алгоритмов
Основные понятия
Численный алгоритм – алгоритм, сводящий решение данной задачи к операциям над числами.
Пример словесного алгоритма Евклида (нахождение наибольшего общего делителя):
1) обозревай a и b и переходи к следующему;
2) сравни обозреваемые числа ( 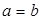 , или
, или 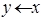 , или
, или 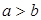 ) и переходи к следующему;
) и переходи к следующему;
3) если обозреваемые числа равны, то каждое из них дает искомый результат, если нет – переходи к следующему;
4) если первое обозреваемое число меньше второго, переставь их местами и переходи к следующему;
5) вычитай второе число из первого и обозревай два числа – вычитаемое и остаток; переходи к указанию 2.
Логический алгоритм – содержит предписания, относящиеся не к цифрам, а к объектам любой природы. Пример – поиск пути в конечном лабиринте.
Программа – процесс последовательного построения заданных величин, идущий в дискретном времени в определенной последовательности.
Алфавит – конечная система символов (букв).
Слово – конечная последовательность букв некоторого алфавита. Например, в алфавите 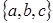 словами будут последовательности b, ac, bac, abbca и т.д. Пустое слово обозначается «Ù» .
словами будут последовательности b, ac, bac, abbca и т.д. Пустое слово обозначается «Ù» .
Подстановка L–M в слове R означает замену словом M всех вхождений слова L в слове R, и наоборот, замену словом L всех вхождений слова M в слове R. Например, подстановка 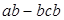 , примененная к слову
, примененная к слову 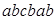 даст слово
даст слово 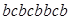 , либо слово
, либо слово 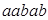 .
.
Эквивалентные слова могут быть получены друг из друга последовательным применением допустимых перестановок.
Стандартные алгоритмы
