Общая характеристика методов решения систем линейных уравнений

Способы решения систем линейных уравнений разделяются на две группы:

1. Точные методы, представляющие собой конечные алгоритмы вычис-ления корней системы.

2. Итерационные методы, позволяющие получать корни системы с заданной точностью путем использования сходящихся бесконечных процессов.

Наиболее известными методами первой группы являются правило Крамера и метод Гаусса. Ко второй группе относятся метод итераций, метод Гаусса-Зейделя, метод релаксации и др.

Вследствие неизбежных округлений результаты даже точных методов являются приближенными, причем оценка погрешности корней в общем случае затруднительна. При использовании итерационных методов к погрешностям корней добавляется погрешность метода.

Интерполяция зависимостей

Одной из важнейших задач процесса математического моделирования является вычисление значений функций, входящих в математическое описание модели. Для сложных моделей подобные вычисления могут быть трудоемкими даже при использовании ЭВМ. При выполнении программ, реализующих основные методы вычислительной математики, большая часть времени также затрачивается на вычисление функций.

Поставленные проблемы решаются путем приближенной замены функции f(x) более простой функцией φ(x), которую нетрудно вычислять при любом значении аргумента х в заданном интервале его изменения. Введенную функцию φ(х) можно использовать не только для приближенного определения численных значений f(x), но и для проведения аналитических выкладок при теоретическом исследовании модели.

Задачей интерполяции в узком смысле считают нахождение приближен-ных значений табличной функции при аргументах х, не совпадающих с узло-выми. Если значение аргумента х расположено между узлами x0 ≤ x ≤ xn то нахождение приближенного значения функции f (x) называют интерполяцией, если аппроксимирующую функцию вычисляют вне интервала [x0, xn], то процесс называют экстраполяцией. Происхождение этих терминов связано с латинскими словами inter - между, внутри, pole - узел, extra - вне.

В более общем плане с помощью интерполяции решают широкий круг задач численного анализа - дифференцирование и интегрирование функций, нахождение нулей и экстремумов функций, решение дифференциальных уравнений и т.д. Возможность решения подобных задач обусловлена достаточно простым видом аппроксимирующей функции φ(х).

Приближенное интегрирование функций.

Общие замечания.

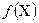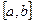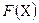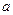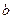Если функция непрерывна на отрезке и известна ее первообразная , то определенный интеграл от этой функции в пределах от до может быть вычислен по формуле Ньютона-Лейбница:

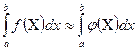(1).

Однако, во многих случаях первообразная функция 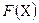не может быть найдена с помощью элементарных средств или является слишком сложной. Вследствие этого вычисление определенного интеграла по формуле (1) может быть затруднительным или даже практически невыполнимым. Кроме того, подынтегральная функция может быть задана таблично и тогда само понятие первообразной теряет смысл. Поэтому, важное значение имеют приближенные и в первую очередь численные методы вычисления определенных интегралов.

Задача численного интегрирования функции заключается в вычислении значения определенного интеграла на основании ряда значений подынтегральной функции. Численное определение однократного интеграла называется механической квадратурой, двойного – механической кубатурой, а соответствующие этим вычислениям формулы называются соответственно квадратурными и кубатурными формулами.

Мы рассмотрим только вычисление однократных интегралов. Обычный прием механической квадратуры состоит в том, что данную функцию 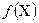на рассматриваемом отрезке 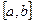заменяют интегрирующей или аппроксимирующей функцией 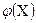простого вида ( например, полиномом ), а затем приближенно полагают:

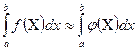(2).

При этом функция 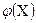должна быть такова, чтобы интеграл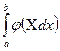

вычислялся непосредственно. На практике наиболее часто кривую, заданную уравнением 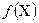, заменяют ломаной или параболой. И, соответственно, интеграл, выражаемый формулой (2), вычисляют методом трапеций методом Симпсона.

5.2. Вычисление определенных интегралов методом трапеций.

Определенный интеграл 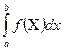численно равен площади криволинейной

трапеции ABCD, которая ограничена осью абсцисс, двумя ординатами 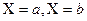и подынтегральной кривой 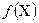(рис.I)

Для вычисления интеграла промежуток 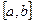делится на n равных частей. Длину каждой части обозначим через h .Тогда получаем 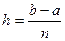;начальное значение 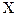равно 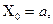абсцисса любой точки деления определится формулой 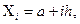значение подынтегральной функции в любой точке деления можно вычислить по формуле 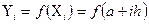. Если даже функция 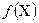задана графически, то значение 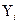можно снять с рисунка.

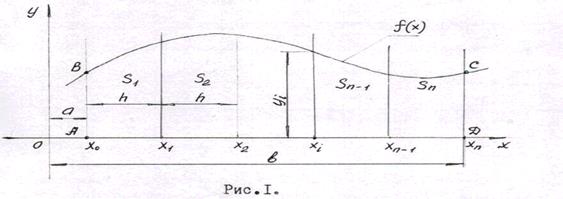
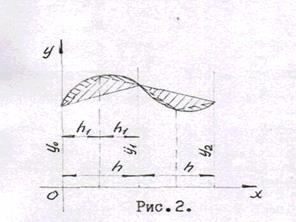
Из рисунка I видно, что площадь криволинейной фигуры ABCD являете:

суммой площадей трапеций 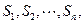высоты которых одинаковы и равны. Следовательно, можно записать

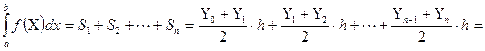
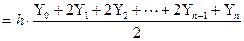
Если в числителе полученной формулы добавить и вычесть крайние ординаты, то получим

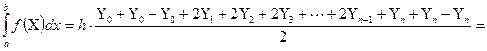
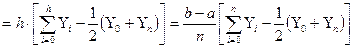(3).

Из рис.2 видно, что формула (3) дает значение площади криволинейной фигуры с недостатком, если кривая выпукла вверх, и с избытком, если крива выпукла вниз. Для уменьшения погрешностей вычисления следует увеличив количество ординат, вводимых в расчет. При большом количестве ординат n

и соответственно при малом шаге h точность формулы (3) возрастает. Однако, ошибки округлен при вычислении значений функции 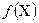.Поэтому оптимальное значение n зависит от того, с каким количеством верных значащих цифр производятся вычисления. Например, в судостроении, где широко применяется метод трапеций, обычно применяют 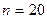. Эта традиция сложилась в те времена, когда все вычисления проводились с помощью арифмометра и логарифмической линейки с точностью до 3-4 значащих цифр.