КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ. 1. Линейная теория упругости
Лабораторная работа №1
РАСТЯЖЕНИЕ УПРУГОЙ ПЛАСТИНЫ
С КРУГОВЫМ ОТВЕРСТИЕМ
КЛЮЧЕВЫЕ СЛОВА
1. Линейная теория упругости
2. Статический анализ
3. Плоская задача (плоское напряженное состояние)
4. Концентрация напряжений
ОПИСАНИЕ ЗАДАЧИ
Тонкая прямоугольная пластина с размерами 2a; a=5 (см) по длине и 2b; b=2 (см) по ширине имеет в центре отверстие радиуса R=0.25 (см) (Рис. 1). Пластина выполнена из упругого изотропного материала с модулем Юнга E=2·106 (кГ/см2) и коэффициентом Пуассона ν=0,3. Пластина растягивается распределенной нагрузкой интенсивности p=0,1·106 (кГ/см2), действующей на ее левую и правую грани. Требуется определить максимальные напряжения в пластине.
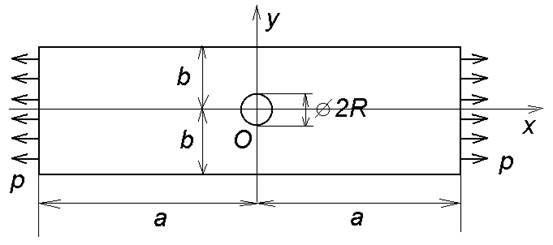
Рис. 1.
ВВОДНЫЕ ЗАМЕЧАНИЯ
Отверстие вносит возмущение в однородное напряженное состояние одноосно растягиваемой пластины. В зоне, вблизи отверстия, происходит повышение напряжений, называемое концентрацией напряжений. Аналогичная задача для бесконечной пластины, одноосно растягиваемой на бесконечности равномерными нагрузками, называется задачей Кирша и является фундаментальной задачей теории упругости о концентрации напряжений. В задаче Кирша максимальные напряжения, равные 3p, возникают в точке с координатами (0, R) (см. рис.1) и являются тангенциальными напряжениями.
Поскольку поля напряжений, деформаций и перемещений являются существенно неоднородными около отверстия, то для получения приемлемой точности конечно-элементных расчетов при построении конечно-элементных сеток следует задавать параметры, обеспечивающие сгущение разбиений вблизи отверстия.
КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ
При плоском напряженном состоянии перемещения пластины в области W, принадлежащей плоскости xy, можно характеризовать вектором перемещений 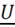 ={Ux, Uy}={U, V}, где U=U(x, y), V=V(x, y). Компоненты
={Ux, Uy}={U, V}, где U=U(x, y), V=V(x, y). Компоненты 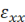 ,
, 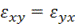 ,
, 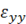 тензора деформаций
тензора деформаций 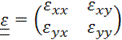 , выражаются через поле перемещений
, выражаются через поле перемещений 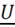 по формулам
по формулам
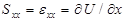 ;
; 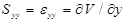 ; (1)
; (1)
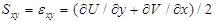
Определяющие соотношения, связывающие механические напряжения и деформации в упругой изотропной среде при плоском напряженном состоянии, имеют вид
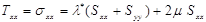
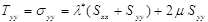 (2)
(2)
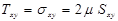
где
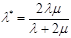 (3)
(3)
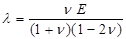 ,
, 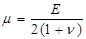 (4)
(4)
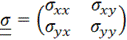 – тензор напряжений,
– тензор напряжений, 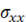 ,
, 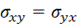 ,
, 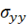 - компоненты тензора напряжений.
- компоненты тензора напряжений.
Коэффициенты l и m из (4) называются коэффициентами Ламе, коэффициент m часто обозначается также через G и имеет смысл модуля сдвига. Модуль E из (4) называется модулем Юнга, а ν – коэффициентом Пуассона.
Уравнения равновесия упругой среды в плоской задаче имеют вид
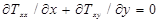 (5)
(5)
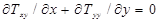 (6)
(6)
Подстановка в (5), (6) определяющих соотношений (2) и формул (1) приводит к эллиптической системе дифференциальных уравнений в частных производных второго порядка относительно неизвестных функций перемещений U и V. К этой системе следует добавить граничные условия на границе 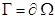 области. Основными видами граничных условий в теории упругости являются следующие условия. Пусть граница G разбита на два подмножества:
области. Основными видами граничных условий в теории упругости являются следующие условия. Пусть граница G разбита на два подмножества: 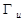 и
и 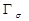 . На части границы
. На части границы 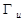 считаются известными компоненты вектора перемещений
считаются известными компоненты вектора перемещений
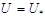 ,
, 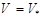 ,
, 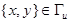 (7)
(7)
На участке 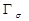 задается вектор напряжений
задается вектор напряжений 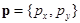
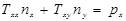
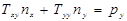 ,
, 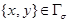 (8)
(8)
где 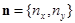 – вектор внешней единичной нормали к границе G.
– вектор внешней единичной нормали к границе G.
Граничные условия (7) носят следующие наименования: граничные условия в перемещениях, граничные условия 1-ого рода, условия типа Дирихле, главные граничные условия. Обычно в (7) 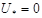 ,
, 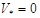 , что соответствует жесткому закреплению участка границы
, что соответствует жесткому закреплению участка границы 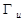 .
.
Аналогично, граничные условия (8) имеют следующие наименования: граничные условия в напряжениях, граничные условия 2-ого рода, условия типа Неймана, естественные граничные условия. При однородных граничных условиях (8), когда 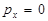 ,
, 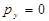 , участок
, участок 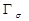 границы называется участком, свободным от напряжений. Вектор напряжений
границы называется участком, свободным от напряжений. Вектор напряжений 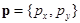 , как векторная функция от x, y, может включать сосредоточенные векторы
, как векторная функция от x, y, может включать сосредоточенные векторы 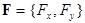 , которые имеют смысл сосредоточенных сил.
, которые имеют смысл сосредоточенных сил.
