Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 4
Задача 1
Определить наибольшее и наименьшее значение функции
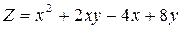
в прямоугольнике 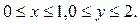
Задача 2
Найти точку, симметричную точке (1,1,1) относительно прямой
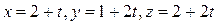
Система координат прямоугольная.
Задача 3
Написать программу для решения следующей задачи. Имеется непустая последовательность целых чисел величиной от 1 до 40, за которой следует 0.
Напечатать все числа, входящие в эту последовательность по одному разу.
Задача 4
Решить задачу

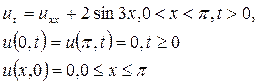
Задача 5
Выяснить, полна ли система A 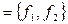 функций алгебры логики
функций алгебры логики
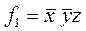 V
V 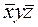 V
V 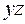 ,
, 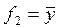
Задача 6
Среди дважды непрерывно дифференцируемых функций y=y(x), заданных на отрезке [0;1] и удовлетворяющих краевым условиям y(0)=1, y(1)=0, есть функция, доставляющая минимум функционалу
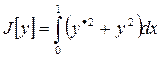
Найти эту функцию.
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11» мая__2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г. 
Вариант № 5
Задача 1
При каких значениях 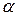 выполняется равенство
выполняется равенство 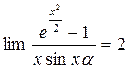 при
при 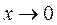
Задача 2
Пусть 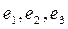 - базис вещественного векторного пространства L и линейный оператор
- базис вещественного векторного пространства L и линейный оператор 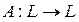 задан в этом базисе матрицей:
задан в этом базисе матрицей:
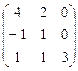
Найти собственные значения и собственные векторы оператора A. Если L обладает базисом из собственных векторов оператора A, найти один из таких базисов и написать матрицу оператора A в найденном базисе.
Задача 3
Написать программу для решения следующей задачи. Имеется целочисленная квадратная матрица 20-го порядка. Определить, является ли она симметричной (относительно главной диагонали).
Задача 4
Решить краевую задачу
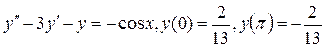
Задача 5
На равномерной сетке с шагом h по x и l по t построить явную разностную схему для задачи
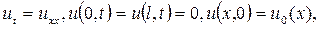
Исследовать ее устойчивость при 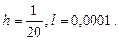
Задача 6
Функция распределения случайной величины  задана формулой
задана формулой
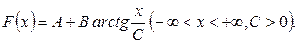
Найти: a) постоянные A и B. б) плотность распределения f(x). в) вероятность того, что величина 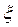 попадает в отрезок [-1;1].
попадает в отрезок [-1;1].
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7) «11»_мая__2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ
Ярославский Государственный Университет им П.Г.Демидова
Факультет ИВТ
ГОСУДАРСТВЕНЫЙ ЭКЗАМЕН 2010г.
Вариант № 6
Задача 1
Вычислить площадь области, ограниченной кривой
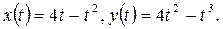
Задача 2
Определить, является ли линейно независимой система векторов
(-2,-1,2,-3); (1,0,1,1); (0,-2,0,-1); (0,2,1,-1).
Если она линейно независима, то вектор (0,0,0,1) представить в виде ее линейной комбинации. В противном случае один из векторов системы представит в виде линейной комбинации остальных трех.
Задача 3
Написать программу для решения следующей задачи. Дано 100 целых чисел.
Определить, сколько из них принимает наибольшее среди этих чисел значение.
Задача 4
Найти общее решение уравнения
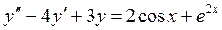
Задача 5
Используя метод касательных (Ньютона), определить с точностью 0,01 корень 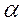 уравнения,
уравнения, 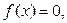 где
где 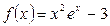 на отрезке [1;2]
на отрезке [1;2]
Задача 6
Плотность распределения случайной величины 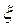 равна
равна
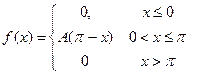
Найти: a) постоянную A;
б) функцию распределения F(x);
в) вероятность того, что величина 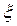 попадает в отрезок [1;2].
попадает в отрезок [1;2].
Утверждено
На заседании ученого совета факультета ИВТ
(протокол № 7 ) «11»_мая__2010 г. Декан_______________
Утверждено
Проректором по учебной работе
«___»___________20___г. ____________________
